Square root of 75
75 is an odd composite number. The square root of 75 is 75 raised to the power half. In this mini-lesson, let us learn about the square root of 75, find out whether the square root of 75 is rational or irrational, and see how to find the square root of 75 by the long division method.
- Square Root of 75: √75 = 8.66
- Square of 75: 752 = 5625
| 1. | What Is the Square Root of 75? |
| 2. | Is the Square Root of 75 Rational or Irrational? |
| 3. | How to Find the Square Root of 75? |
| 4. | FAQs on Square Root of 75 |
What Is the Square Root of 75?
- The square root of 75 can be written as √75.
- It means that there is a number a such that a × a = 75. It can also be written as: a2 = 75.
- a = √75. a is the 2nd root of 75 and a = 8.66
- The square root of any number has two values; one is positive and the other is negative. So, √75 = +8.66 or - 8.66
- In the exponential form, we denote √75 as (75) ½
- We know that 75 = 5 × 5 × 3. In the simplest radical form √75 = 5√3
Is the Square Root of 75 Rational or Irrational?
The square root of 75 is an irrational number where the numbers after the decimal point go up to infinity. √75 = 8.660.√75 cannot be written in the form of p/q, hence it is an irrational number.irrational with never-ending digits.
How to Find the Square Root of 75?
The square root of 75 or any number can be calculated in many ways. Two of them are the average method and the long division method.
Square Root of 75 by Average Method
- Take two perfect square numbers which are just smaller than 75 and just greater than 75. √64 < √75 < √81
- 8 < √ 75 < 9
- Using the average method, divide 75 by 8 or 9.
- Let us divide by 9. 75 ÷ 9 = 8.33
- Find the average of 8.33 and 9
- (8.33+9) / 2 = 17.33 ÷ 2 = 8.66
- √75 ≈ 8.66
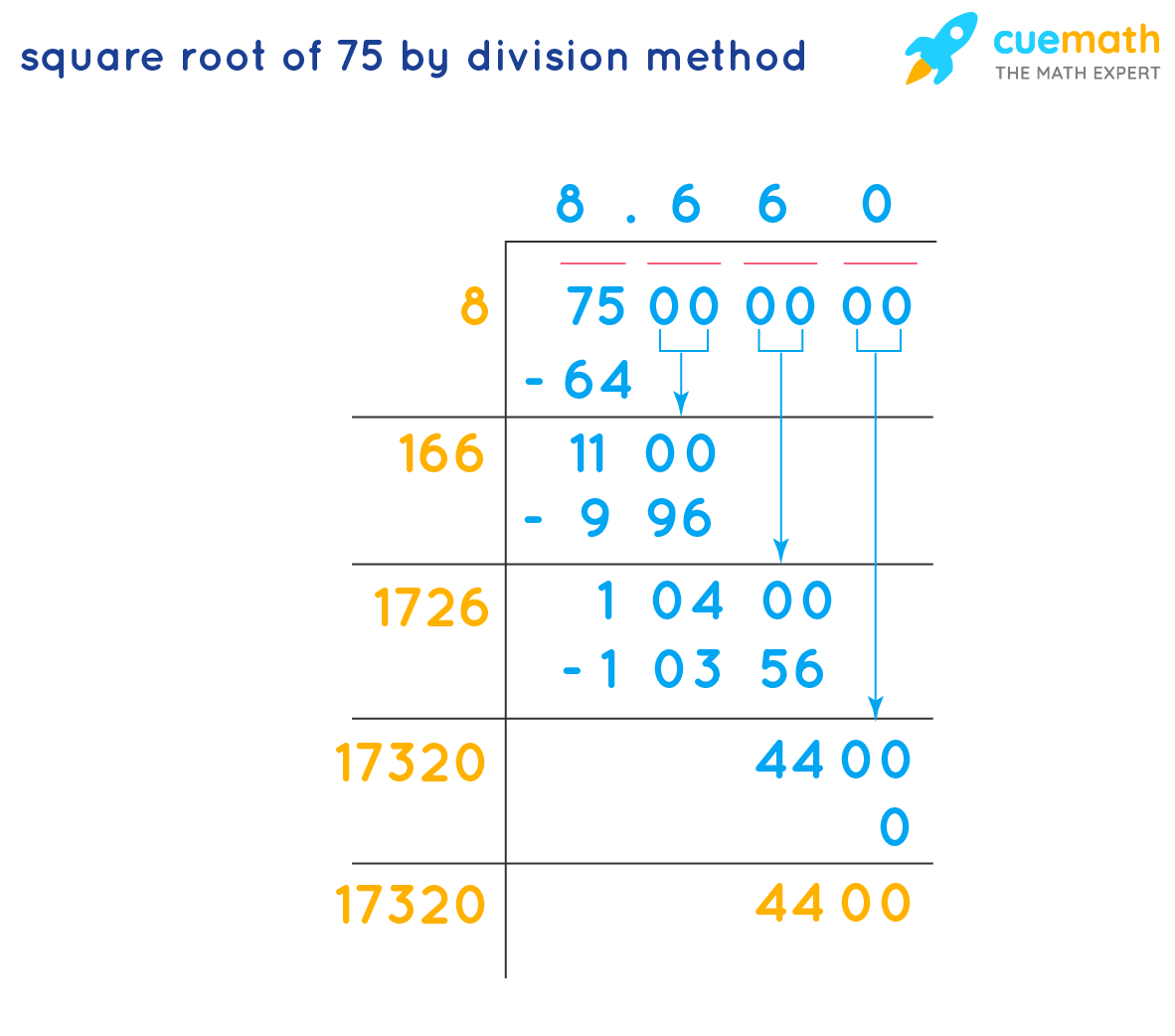
Square Root of 75 by Long Division Method
The long division method helps us to find a more accurate value of square root of any number.
Let's see how to find the square root of 75 by the long division method.
- Step 1: Express 75 as 75.000000. We take the number in pairs from the right. Take 75 as the dividend.
- Step 2: Now find a quotient which is the same as the divisor. Multiply quotient and the divisor and subtract the result from 75.
- Step 3: Now double the quotient obtained in step 2. Here is 2 × 8 = 16. 160 becomes the new divisor.
- Step 4: Apply decimal after quotient '8' and bring down two zeros. We have 1100 as the dividend now.
- Step 5: We need to choose a number that while adding to 160 and multiplying the sum with the same number we get a number less than 1100. 160+ 6 =166 and 166 × 6 = 996. Subtract 996 from 1100. We get 104.
- Step 6: Bring down two zeros again and place it after 104, so that it becomes 10400 which is the new dividend. Now multiply the number in the quotient by 2. Here it is 86. We get 172. Have it as 1720. Now find a number at the unit's place of 1720 multiplied by itself gives 10400 or less. We find that 1726 × 6 = = 10356. Find the remainder.
- Step 6: Repeat the process until we get the remainder equal to zero. The square root of 75 up to two places is obtained by the long division method. Thus √75 = 8.66
Explore square roots using illustrations and interactive examples.
Tips and Tricks
- The square root of any number can be assumed to be between the square root of the two nearest perfect squares of that number. For example, the square root of 75 lies between the square root of 64 and 81. √64 < √56 < √81, i.e., 8 < √75 < 9. Use the average method then, to find the approximate value.
- We just multiply 75 with 3 to make it a perfect square. This is because, 75 = 5 × 5 × 3. 3 doesn't have a pair. Thus 75 × 3 = 225 and √225 is 15.
Important Notes
- The square root of 75 is 8.660 approximated to 3 decimal places.
- The simplified form of√75 in its radical form is 5√3
- √75 is an irrational number.
Square Root of 75 Solved Examples
-
Example 1: Evaluate √75 + √108
Solution:
√75 = √(25 × 3) = 5 √3
√108 =√(36 × 3) = 6 √3
√75 + √108 = 5 √3 + 6 √3
= (6 + 5)√3 = 11 √3
Thus √75 + √108 = 11 √3
-
Example 2: Find the real-number root of √(75/64)
Solution:
√(75/4) =√(75/√(64)
5√3 / 8 = 5/8 √3
-
Example 3: Evaluate: √75 ×√15
Solution:
√75 = (5 × 5 × 3) = √(52 × 3) = 5√3
√45 = √(3 × 3 × 5) = √(32 × 5 ) = 3√5
√75 × √45 = 5√3 × 3√5 = 5 × 3 × √3 × √5 = 15 × √15 = 15√15

FAQs on Square Root of 75
What is the square root of 75?
The square root of 75 is approximately equal to 8.66.
How do you write square root of 75 in its simplified form?
5√3 is the simplest form of√75.
75 is the square root of which number?
75 is the square root of 5625.
Is √75 a rational number?
√75 is an irrational number, because the value of √75 is a non-teminating decimal.
How to find the square root of 75?
The accurate value of √75 can be evaluated using the long division method.
visual curriculum