Square Root of 60

The square root of 60 is expressed as √60 in the radical form and as (60)^½ or (60)^0.5 in the exponent form. The square root of 60 rounded up to 10 decimal places is 7.7459666924. It is the positive solution of the equation x² = 60. We can express the square root of 60 in its lowest radical form as 2 √15.

• Square Root of 60: 7.745966692414834
• Square Root of 60 in exponential form: (60)^½ or (60)^0.5
• Square Root of 60 in radical form: √60 or 2 √15

The square root of any number n can be written as √n. It means then there is a number a such that: a × a = n. Now it can also be written as:  a² = n or removing the squares on both the sides, we get a = √n . So, a is called as second root of n.

• Now, if n = 60, then a = √60 is the square root of 60. In the simplest radical form, √60 = √4 x 15 = 2√15
• The decimal form of √60 = 7.74

The square root of 60 is an irrational number with never-ending digits. √60 = 7.7459666924148. The square root of 60 can not be written in the form of p/q, hence it is an irrational number.

Square Root of 60 by Approximation

• Take two perfect square numbers which are just smaller than 60 and just greater than 60.
• √49 = 7 < √60 and  √64 = 8 > √60
• 7 < √60 < 8
• Multiply the inequality by 10.
• 70 < 10 √60 < 80 
• √4900 < √6000 <√6400
• Move more closer to the inequality
• √5929 < √6000 < √6084
• 77 < 10√60 < 78
• Divide both sides by 10.
• 7.7 < √60 < 7.8 
• Take the average of both lower and upper limits
• √60 ≈ (7.7 +7.8)/ 2
• √60 ≈ 7.75

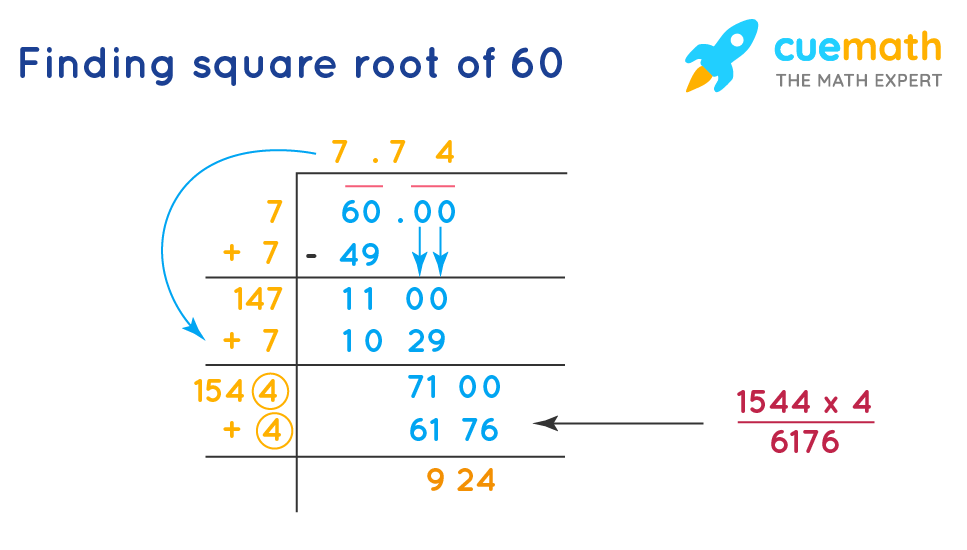
Square Root of 60 by Long Division Method

The long division method helps us to find the accurate value of the square root of any number. Let's see how to find the square root of 60 by the long division method.

• Step 1: Find a number such that when we multiply the number by itself the product is less than 60. 7 × 7 = 49
• Step 2: Take the same number as the quotient which is the divisor, 7. multiply the quotient and the divisor and subtract the result from 60
• Step 3: Take the same quotient '7' and add with the divisor '7'.
• Step 4: Apply decimal after quotient '7' and bring down two zeros and place it after 11 so that it becomes 1100. We need to find a new divisor 14X  such that the digit placed in X(units place of our new divisor) multiplied to itself gives a number less than 1100, our new dividend. 147 × 7 = 1029. Complete the process of division.
• Step 5: Bring down two zeros again and place it after 71, so that it becomes 7100.  Take 7 and add it to 147. 147 + 7 = 154. We need to identify a number X so that when placing it at the end of 154X and multiplying the result with the same number we get a number less than 7100. 1544 × 4 = 6176. Write the same number after 7 in the quotient. Complete the process of division.
• Step 6: Repeat the process to find the square root of 60. The square root of 60 up to two places is obtained by the long division method. is 7.74

Explore Square roots using illustrations and interactive examples

• Square root of 10
• Square root of 16
• Square root of 30
• Square root of 56
• Square root of 65

• √60 = √4 × 15 = 2√15
• √60 = + 7.7459666 and √60 = - 7.7459666

• Find the square root of 600 up to 3 decimal places by approximation method.
• Find the smallest 6 digit perfect square number.
• Chris wants to find out the value of 12 in terms of a and b,If the value of √√60 = a and √√5= b, help him to pick the correct option.