Square Root of 56

Squares and square roots are special exponents. When the exponent on the number is 2, it is termed as square and when the exponent is ½ it is called a square root of a number. Let's see how to find the square root of 56 and also discover interesting facts around them. Think of a number that gives 56 on squaring? n² = 56. What could be n? In this mini lesson, let us learn about the square root of 56, find out whether the square root of 56 is rational or irrational, and see how to find the square root of 56 by long division method. 

• Square Root of 56: √56 = 7.483
• Square of 56: 56² = 3136

The square root of any number n can be written as √n. It means then there is a number a such that: a × a = n. Now it can also be written as: a² = n. a = √n. a is the 2nd root of n. Now, if n = 56, then a = √56 is the square root of 56. In the radical form, the square root of 56 can be represented by √56. The simplest radical form of square root of 56 is√56 = √(4 × 14) = 2 √14.

The square root of 56 is an irrational number where the numbers after the decimal point go up to infinity. √56 = 7.483314....The square root of 56 can not be written in the form of p/q, hence it is an irrational number. Only the square root of numbers which are perfect squares like, 9, 16, 25, 100 are rational numbers, but the square root of numbers which are not a perfect square is irrational with never-ending digits. The square root of any number has two values, one is positive and the other is negative. So, √56 = + 7.483314 and - 7.483314

The square root of 56 or any number can be calculated in many ways. Two of them are approximation (hit and trial) and the long division method. Let's see how to find √56 by the approximation method:

• Take two perfect square numbers which are just smaller than 56 and just greater than 56. √49 < √56 < √64
• 7 <  √ 56 < 8
• Multiply the inequality by 10
• 70 < 10 √56 < 80
• √ 4900 < √5600 < √ 6400
• Move more closer to the inequality 
• √ 5476 < √5600 < √ 5625
• 74 < 10 √ 56 < 75
• Divide both sides by 10
• 7.4 < √ 56 < 7.5
• Take the average of both lower and upper limits.
• √56 ≈ (7.4 + 7.5) / 2
• √56 ≈  7.45

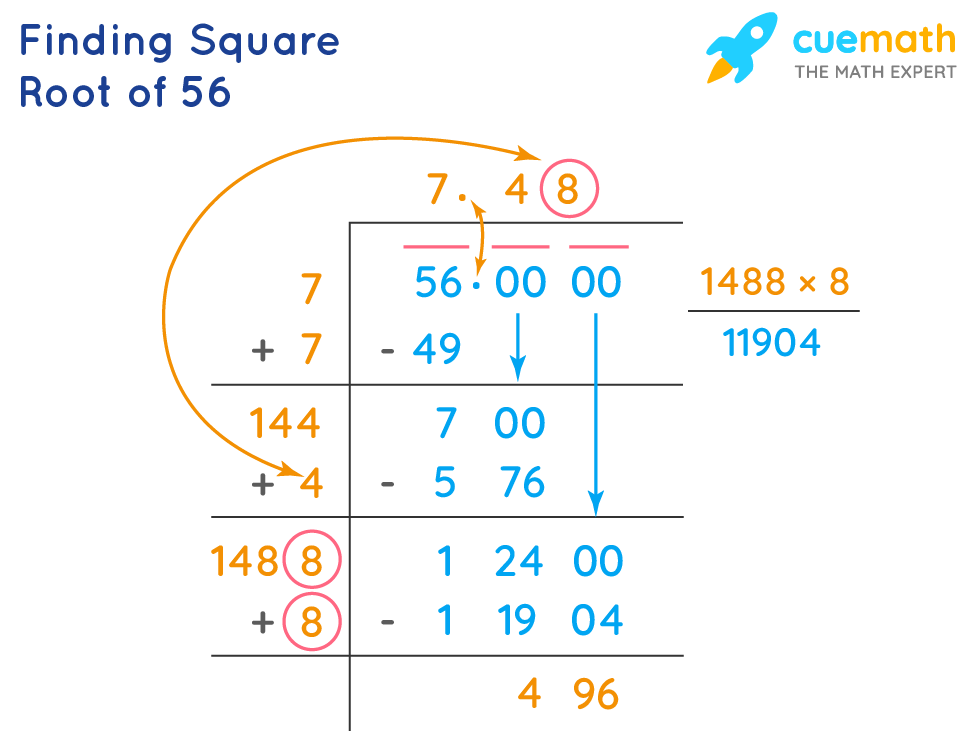
Square Root of 56 by Long Division Method

The long division method helps us to find a more accurate value of square roots of any number.

Let's see how to find the square root of 56 by the long division method.

• Step 1: Divide the number 56 by 7 (because 7² = 49 is a perfect square number just less than 56)
• Step 2: Take the same number as quotient which is the divisor, 7. multiply quotient and the divisor and subtract the result from 56
• Step 3: Take the same quotient '7' and add with the divisor '7'.
• Step 4: Apply decimal after quotient '7' and bring down two zeros and place it after 7 so that it becomes 700. We need to take a number that when placing it at the end of 14 and multiplying the result with the same number we get a number less than 700. 144 × 4 = 576. Subtract 576 from 700. 700 - 576 = 124
• Step 5: Bring down two zeros again and place it after 124, so that it becomes 12400. Take 4 and add it to 144. 144 + 4 = 148. We need to take a number that when placing it at the end of 148 and multiplying the result with the same number we get a number less than 12400. 1488 × 8 = 11904. Write the same number after 4 in the quotient. Subtract 11904 from 12400. 12400 - 11904 = 496. 
• Step 6: Repeat the process until we get the remainder equal to zero. The square root of 56 up to two places is obtained by the long division method.

Explore Square roots using illustrations and interactive examples

• Square root of 36
• Square root of 54
• Square root of 16
• Square root of 26
• Square root of 60

The square root of any number can be assumed to be between the square root of two nearest perfect squares of that number. For example, the square root of 56 lies between the square root of 49 and 64
√49 < √56 < √64, i.e., 7 < √56 < 8

What is the square root of 56?

The square root of 56 is approximately equal to 7.48

How do you write square root of 56 in its simplified form?

2√14 is the simplest form of √56.

56 is the square root of which number?

56 is the square root of 3136.

Is √56  a rational number?

√56  is an irrational number, because the value of √56 is a non-teminating decimal.

How to find the square root of 56?

The accurate value of √56 can be evaluated using the long division method and the value obtained is 7.48331477355