Alternate Segment Theorem
The segment of a circle is the region between a chord and the corresponding arc of the circle. When a chord is drawn, it creates a major segment and a minor segment in the circle.
Let's observe the figure given below, in which DE is the tangent and BC is a chord. \(\angle\) BCE is made by the tangent and chord BC. This is equal to \(\angle \)BAC in the alternate segment.
\(\angle\) ACD is made by the tangent DE and chord AC. This is equal to \(\angle \) ABC in the alternate segment.
This is what the alternate segment theorem states. According to this theorem, the angle formed between the tangent and the chord through one of the end points is equal to the measure of the angle opposite in the alternate segment.

Lesson Plan
What Do You Mean by the Alternate Segment Theorem ?
Alternate Segment Theorem
For any circle, the angle between a tangent and a chord through the point of contact of the tangent is equal to the angle made by the chord in the alternate segment.
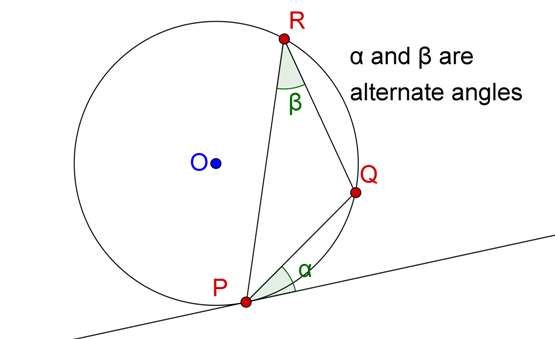
Suppose that a tangent is drawn to a circle such that the point of contact is P, and through P, a chord PQ is drawn which is inclined to the tangent at an angle \(\alpha\).
Suppose that PQ subtends an angle \(\beta\) at a point R anywhere on the circumference of the circle, as shown:
Let \(\angle PRQ = \angle \beta \) , the alternate angles in the alternate segment for the angle between the tangent at P and the chord PQ.
This angle will be the same regardless of the position of R (as long as R stays in the segment opposite the tangent).
Alternate Segment Theorem Examples
Consider the figures given below. On the left, we have three valid alternate angles in the alternate segment (and all of them will be equal) for the tangent at P and the chord PQ, whereas, on the right, the angle marked \(\gamma\) is not the alternate angle for the tangent at P, since it is on the same side of the chord PQ (same segment) as the tangent at P.
Alternate Segment Theorem Proof
The angle between the chord and the tangent is equal to the angle made by the chord in the alternate segment.
Let's prove this.

Let P be the point on the circumference of the circle. O be the center of the circle.
\(\overline{AB}\) is the tangent passing through the point P.
The tangent makes \(\angle \alpha\) with the chord PQ.
Consider an \(\angle PRQ =\beta\) in the alternate segment.
Now, let's prove \(\angle \alpha = \angle \beta\).
\(\overline{OP} = \overline{OQ} (\because\) both are the radii of the circle.)
\(\angle OPQ = \angle OQP\) \((\because\) the angles opposite to the equal sides are equal.)
\(\because \triangle OPQ\) is isosceles,
\[\begin{align} \angle POQ &= 180^{\circ} -\angle OPQ - \angle OQP\\\\ &= 180^{\circ} - 2 \angle OPQ ---- (1)\end{align}\]
\(\because \overline {AB}\) is the tangent,
\[\begin{align} \angle OPB &=90^\circ \\ \Rightarrow \alpha &= 90^{\circ} - \angle OPQ ---- (2) \end{align}\]
From (1) and (2), we find that \[\angle POQ = 2\alpha\]
We know that the angle at the center is twice the angle at the circumference.
\[\begin{align}\angle POQ &= 2\angle PRQ\\\\\angle PRQ &= \dfrac{1}{2}\angle POQ\\\\\angle \beta &=\dfrac{1}{2}(2 \alpha)\\\\ &= \angle \alpha \end{align}\]
Thus, the alternate segment theorem is proved.

- Identify the chord which makes the angle with the tangent and locate the angle in the alternate segment of the chord.
- To find the missing angles inside the polygon inscribed in the circle, use the trick of finding the angles in the alternate segment.
Using Alternate Segment Theorem to Find Angles
Alternate Segment Theorem Quadrilateral

This theorem is used to show that it is extended to the alternate segment theorem quadrilateral too.
Here, we know that by alternate segment theorem, \[\angle p = \angle r\]
We need to show that \(\angle s = \angle q\)
As the line tangent LM is straight, we have
\[\angle p + \angle s = 180----(1)\]
As angles \(\angle r\) and \(\angle q\) are opposite angles in a cyclic quadrilateral, we know that
\[\angle q + \angle r = 180----(2)\]
\[\angle p + \angle s = \angle q + \angle r\]
\(\because \angle p = \angle r\), we have \(\angle s = \angle q\)
Hence proved.

- The alternate segment theorem states that the angle made by the chord and the tangent is equal to the angle made by the chord in the alternate segment.
- This theorem helps us to find the unknown angles of any polygon inscribed in the circle.
Solved Examples
| Example 1 |
Given that BC is the chord that makes \(68 ^{\circ}\) with the tangent PQ. Find all the missing angles.
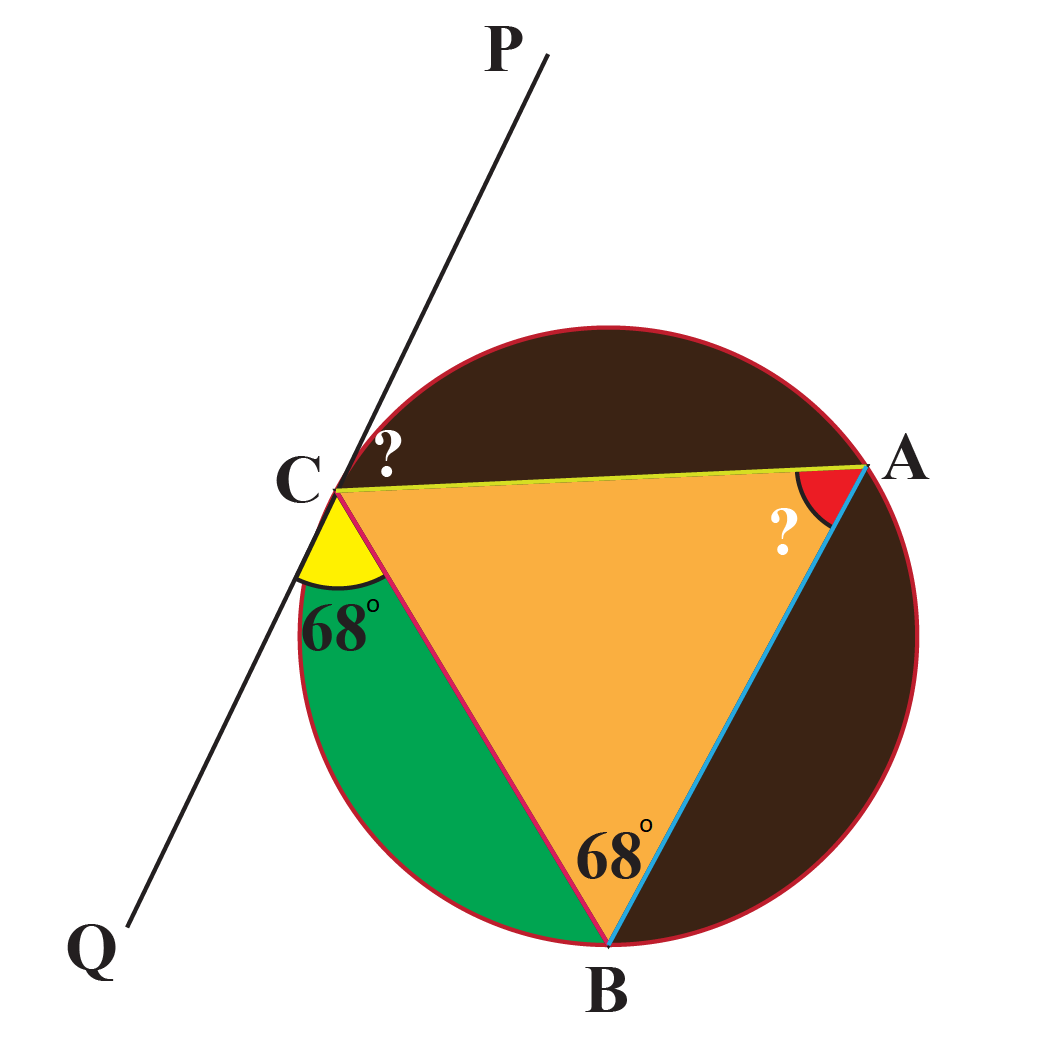
Solution
| Statement | Reason |
|---|---|
| \(\angle CAB = 68 ^{\circ}\) | Angle in the alternate segment |
| \(\angle PCA = 68 ^{\circ}\) | Angle in the alternate segment |
|
\(\therefore \angle CAB = 68 ^{\circ}\) \(\angle PCA = 68 ^{\circ}\) |
| Example 2 |
Find the angles x and y in this circle.

Solution
We use the alternate segment theorem to find the unknown angles.
| Statement | Reason |
|---|---|
| \(\angle BAC = 90^{\circ}\) | Angle in a semicircle is \(90^{\circ}\). |
|
\(\angle ACB = 30^{\circ}\) |
Given |
| \(\angle ABC = 60^{\circ}\) | Sum of angles in a triangle = \(180^{\circ}\) |
| x = \( 60^{\circ}\) | The angle made by the chord and the tangent is equal to the angle in the alternate segment. |
| \(\therefore\) \(\angle x = \angle y = 60^{\circ}\) |
Interactive Questions
Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.
Let's Summarize
We hope you enjoyed learning about alternate segment theorem with interactive questions. Now, you will be able to easily solve problems on the alternate segment theorem or the tangent chord theorem quadrilateral and find the angles in alternate segment.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.
FAQs on Alternate Segment Theorem
1. What is called an alternate angle?
When a transversal intersects two or more parallel lines, we get alternate angles that are in the opposite positions relative to a transversal intersecting the lines.
2. What is a circle theorem?
The circle theorem states that a perpendicular from the center of the circle to a chord will always bisect the chord.
3. What is an example of a line segment in real life?
The edges of a book form a quadrilateral which is made of four line segments.
4. What is the equation for alternate interior angles?
If two angles A and B are the alternate interior angles, they are represented as \(\angle A \cong \angle B\).
5. What is the angle in the alternate segment theorem?
The alternate segment theorem states that in a circle, the angle which lies between a chord and a tangent through any of the end points of the chord is equal to the angle in the alternate segment.
6. What is another name for the angle segment theorem?
Another name for the angle segment theorem is the tangent-chord theorem.
7. Is there only one way to solve alternate segment theorem?
There are 2 ways to solve the alternate segment theorem. One way is to solve using the central angle circle theorem and the other is by creating 3 isosceles triangles.
8. What is the central angle theorem?
The central angle theorem states that the central angle from two chosen points on the circle is always twice the inscribed angle from those two points.
9. Why is the alternate segment theorem called a circle theorem?
We have 6 circle theorems and the alternate segment is one of them. This theorem states that the angle between a tangent and a chord through the point of contact of the tangent is equal to the angle made by the chord in the alternate segment.
10. What do you mean by the alternate segment?
When a chord is drawn in a circle, it forms two segments. The segment which is located on the opposite side of the segment that is made by that particular chord and the arc is called the alternate segment.