Inverse Variation
Inverse variation is a type of proportionality where one quantity decreases while the other increases or vice versa. This implies that the magnitude or the absolute value of one quantity decreases if the other quantity increases such that their product will always remain the same. This product is also known as the constant of proportionality.
Inverse variation represents an inverse relationship between two quantities. There are several real-life applications of inverse variation. For example, if the speed of a car increases, the time taken to reach the destination decreases. In this article, we will elaborate on inverse variation, its formula, graph, and various examples.
| 1. | What is Inverse Variation? |
| 2. | Inverse Variation Formula |
| 3. | Inverse Variation Graph |
| 4. | Inverse Variation Table |
| 5. | FAQs on Inverse Variation |
What is Inverse Variation?
Inverse variation establishes a proportionality between two quantities that follow an inverse relationship. There are two types of proportionalities. These are direct variation and inverse variation. Two quantities are said to be directly proportional to each other if an increase or decrease in one quantity leads to a corresponding increase or decrease in the other quantity. This is in contrast to an inverse variation where one quantity increases with a decrease in the other.
Inverse Variation Definition
Two non-zero quantities are said to be in an inverse variation if their product yields a constant term (constant of proportionality). In other words, two quantities follow inverse variation if one quantity is directly proportional to the reciprocal of the other quantity. This means that an increase in one quantity leads to a decrease in the other while a decrease in one quantity leads to an increase in the other.
Inverse Variation Example
Suppose x and y are in inverse variation. It is given that x = 10 and the constant of proportionality equals 50. Then the value of y will be 50 / 10 = 5.
Inverse Variation Formula
The symbol "\(\propto\)" is used to indicate proportionality. If two quantities x and y follow an inverse variation then they are represented as follows:
x \(\propto\) \(\frac{1}{y}\) or y \(\propto\) \(\frac{1}{x}\)
To convert this expression into an equation, a constant or coefficient of proportionality needs to be introduced. Thus, the formula for inverse variation is given as follows:
x = \(\frac{k}{y}\) or y = \(\frac{k}{x}\)
xy = k
Here, k is the constant of proportionality. Also, x \(\neq\) 0 and y \(\neq\) 0
Product Rule for Inverse Variation
Suppose the two solutions of inverse variation are (\(x_{1}\), \(y_{1}\)) and (\(x_{2}\), \(y_{2}\)).
This can also be expressed as \(x_{1}\) \(y_{1}\) = k and \(x_{2}\) \(y_{2}\) = k.
Using these two equations,
\(x_{1}\) \(y_{1}\) = \(x_{2}\) \(y_{2}\) or \(\frac{x_{1}}{x_{2}}\) = \(\frac{y_{2}}{y_{1}}\)
This is the product rule for inverse variation.
Let us understand this inverse variation formula with the help of an example.
Example: Suppose x and y are in an inverse proportion such that, when x = 15, then y = 4. Find the value of y when x = 20.
Solution:
Given: \(x_{1}\) = 15, \(y_{1}\) = 4, \(x_{2}\) = 20, \(y_{2}\) = ?
Using inverse variation formula,
\(x_{1}\)\(y_{1}\) = \(x_{2}\) \(y_{2}\)
⇒ 15 × 4 = 20 × \(y_{2}\)
⇒ 60 = 20 × \(y_{2}\)
⇒ \(y_{2}\) = 3
Answer: Thus, the value of y is 3, when x is 20.
Inverse Variation Graph
The graph of an inverse variation is a rectangular hyperbola. If there are two quantities x and y that are in inverse variation then their product will be equal to a constant k. As neither x nor y can be equal to zero thus, the graph never crosses the x-axis or y-axis. The graph of an inverse variation with the function y = k / x is given below:
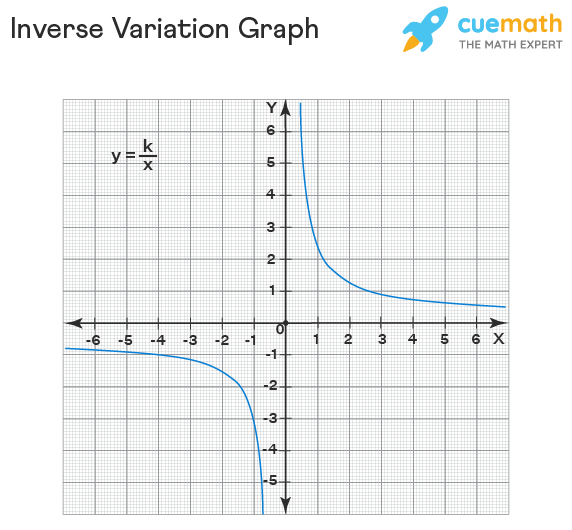
Inverse Variation Table
An inverse variation table is used to examine how one quantity changes with a change in another quantity that follow an inverse proportionality. Suppose two quantities x and y are in an inverse variation given by y = 18 / x. Then the inverse variation table can be given as follows:
| x | y = 18 / x |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
| -3 | -6 |
| -2 | -9 |
| -1 | -18 |
Related Articles:
Important Notes on Inverse Variation
- If one quantity decreases while another increases and vice versa, then both quantities are said to follow an inverse variation.
- An inverse variation is represented as x \(\propto\) \(\frac{1}{y}\) or x = \(\frac{k}{y}\).
- Both quantities that follow an inverse variation should not be equal to 0 and their product is equal to a constant (constant of proportionality).
- Two quantities following an inverse variation will result in a rectangular hyperbola in the cartesian coordinate plane.
Examples on Inverse Variation
-
Example 1: Find the constant of proportionality if x = 12 and y = 4 follow an inverse variation.
Solution: As x and y are in inverse variation thus, xy = k
(12)(4) = 48 = k
Answer: Constant of proportionality k = 48 -
Example 2: If 12 workers complete a job in 5 hours, how much time will 10 workers take to complete the same job?
Solution: Let x be the number of workers and y be the time taken to complete the job. The time taken to finish the work will increase if the number of workers decreases. Thus, this is a case of inverse variation. Using the product rule,
\(\frac{x_{1}}{x_{2}}\) = \(\frac{y_{2}}{y_{1}}\)
\(\frac{12}{10}\) = \(\frac{y}{5}\)
y = 6 hours
Answer: 10 workers will take 6 hours to complete the job. -
Example 3: If the constant of proportionality equals 7 and y = 14, what will be the value of x when x and y are in inverse variation?
Solution: As x and y are in inverse variation thus, xy = k
x = k / y
x = 7 / 14 = 0.5
Answer: x = 1 / 2 or 0.5

FAQs on Inverse Variation
What Does Inverse Variation Mean?
Inverse variation refers to the relationship between two quantities wherein one increases while the other correspondingly decreases or vice versa. Both are non-zero quantities and their product is the constant of proportionality.
What is the Formula for Inverse Variation?
The formula for inverse variation is xy = k. The product rule of inverse variation is given by \(\frac{x_{1}}{x_{2}}\) = \(\frac{y_{2}}{y_{1}}\).
What is an Example of Inverse Variation?
Suppose a certain number of pipes are used to fill a tank. If the number of pipes is increased then the time taken to fill the tank will reduce. Thus, the number of pipes and the time taken to fill the tank are an example of inverse variation.
How to Graph Inverse Variation?
The graph of an inverse variation is a rectangular hyperbola. In the given inverse variation function of the form y = k / x, substitute values of x to get the corresponding values of y. The test points so obtained can be plotted on a cartesian plane to get the graph of an inverse variation.
How to Find the Constant of Inverse Variation?
By multiplying the two quantities in inverse variation, the constant of proportionality can be obtained. This is expressed as xy = k.
Is xy = 12 an Inverse Variation?
Yes, xy = 12 is an inverse variation. This can be given as x = 12 / y. If the constant 12 is removed then x \(\propto\) \(\frac{1}{y}\). This implies that when x increases y decreases and vice versa.
What is the Difference Between Direct and Inverse Variation?
When one quantity increases with an increase in another quantity it is known as direct variation. This is expressed as y \(\propto\) x or y / x = k. In an inverse variation, one quantity increases while the other decreases. This is represented as x \(\propto\) \(\frac{1}{y}\) or xy = k.
visual curriculum