Parametric Form of Parabolas

PARAMETRIC FORM OF \({y^2} = 4ax\) : The parabola \({y^2} = 4ax\) is a lot of times specified not in the standard x – y form of but instead in a parametric form, i.e., in terms of a parameter, say t.

The equation \({y^2} = 4ax\) can be equivalently written in parametric form

\[x = a{t^2},\,y = 2at\]

This is easily verifiable by substitution. Thus, for any value of t, the point \(\left( {a{t^2},{\rm{ }}2at} \right)\)will always lie on the parabola \({y^2} = 4ax\) Different values of referred to as simply the point give rise to different points on the parabola.

The point \(\left( {a{t^2},{\rm{ }}2at} \right)\) is many times referred to as simply the point t.

Example – 6

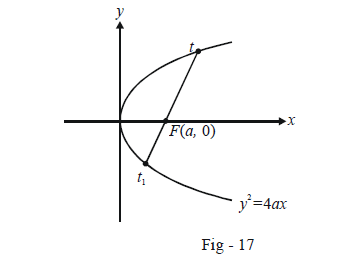
From a point t on \({y^2} = 4ax\) a focal chord is drawn. Find the other end-point of this chord.

Solution: Let the other end-point be the point \({t_1}\). Thus, the co-ordinates of the two ends of the chord are\(\left( {a{t^2},{\rm{ }}2at} \right)\) and \((at_1^2,\,\,2a{t_1})\) .

The equation of this chord is therefore

\[\frac{{y - 2at}}{{x - a{t^2}}} = \frac{{2at - 2a{t_1}}}{{a{t^2} - at_1^2}} \qquad \qquad \dots\left( 1 \right)\]

Since this chord is a focal chord, the coordinates of F, i.e. (a, 0) must satisfy (1)

\[\begin{align}&\Rightarrow \qquad \frac{{ - 2at}}{{a - a{t^2}}} = \frac{{2a(t - {t_1})}}{{a({t^2} - t_1^2)}}\\
&\Rightarrow \qquad \frac{{ - t}}{{1 - {t^2}}} = \frac{1}{{t + {t_1}}}\\&\Rightarrow \qquad - {t^2} - t{t_1} = 1 - {t^2}\\ &\Rightarrow \qquad \fbox{\({tt_1}\) = - 1}\end{align}\]

This very widely used result simply states that the product of the two end-points \(t{\rm{ }}\;\;and\;\;{\rm{ }}{t_1}\) of any focal chord will be –1.

Example – 7

Let O be the origin and AB be any focal chord of the parabola \({y^2} = 4ax.\) A is the point t. Find

(a) the minimum area of \(\Delta OAB\)

(b) the locus of the centroid of \(\Delta OAB\)

Solution: Since AB is a focal chord, the point B is \(\begin{align} - \frac{1}{t}\end{align}\) . Thus, the co-ordinates of A and B are \(\left( {a{t^2},{\rm{ }}2at} \right)\) and \(\left( {\begin{align}\frac{a}{{{t^2}}},\,\, - \frac{{2a}}{t}\end{align}} \right)\) respectively.

\(\begin{align}(a) \;\;{\rm{area}}\;(\Delta OAB){\rm{ }} &= \frac{1}{2}{\mkern 1mu} {\mkern 1mu} \left| {\begin{array}{*{20}{c}} {a{t^2}\;\;\;\frac{a}{{{t^2}}}\;\;\;0}\\ {2at\;\;\; - \frac{{2a}}{t}\;\;\;0}\\ {1\;\;\;1\;\;\;1} \end{array}} \right|
&\rm{(Expanding\,along\,C3)}\\&= \frac{1}{2}\left\{ { - 2{a^2}t - \frac{{2{a^2}}}{t}} \right\}\\&= - {a^2}\left\{ {t + \frac{1}{t}} \right\}\end{align}\)

From calculus, we can easily deduce that the magnitude of \(t + \begin{align}\frac{1}{t}\end{align}\) is minimum when \(t = \pm 1\) the minimum magnitude is hence 2: Thus, the minimum area of \(\Delta OAB\) is \(2{a^2}\). This occurs when AB is the LR, as might have been expected by symmetry.

(b) Let (h, k) be the co-ordinates of the centroid of \(\Delta OAB\) .

We have,

\[\begin{align}&\qquad h = \frac{{a{t^2} +\begin{align} \frac{a}{{{t^2}}}\end{align} + 0}}{3},k = \frac{{2at - \begin{align}\frac{{2a}}{t}\end{align} + 0}}{3}\\ &\Rightarrow \quad {t^2} + \frac{1}{{{t^2}}} = \frac{{3h}}{a},t - \frac{1}{t} = \frac{{3k}}{{2a}}\end{align}\]

Squaring the second relation, we obtain

\[{t^2} + \frac{1}{{{t^2}}} - 2 = \frac{{9{k^2}}}{{4{a^2}}}\]

Using the first relation in this,

\[\begin{align}& \qquad \frac{{3h}}{a} - 2 = \frac{{9{k^2}}}{{4{a^2}}}\\\\&\Rightarrow \quad12ah - 8{a^2} = 9{k^2}\\\\&\Rightarrow \quad 4a\left( {h - \frac{{2a}}{3}} \right) = 3{k^2}\end{align}\]

We now use (x, y) instead of ( h, k); the locus of the centroid is

\[3{y^2} = 4a\left( {x - \frac{{2a}}{3}} \right)\]