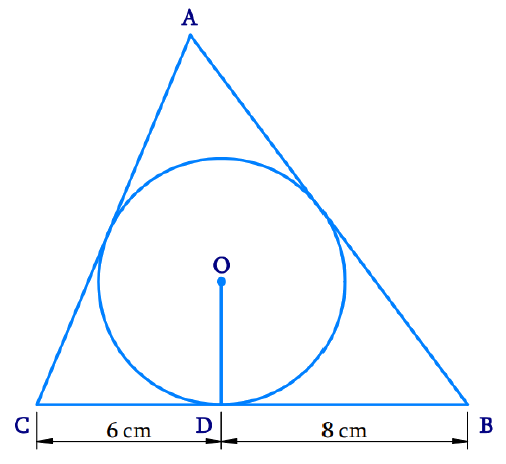
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC
Solution:
Given: Triangle ABC is drawn to circumscribe a circle of radius 4 cm.

From the diagram, BD = 8 cm, CD = 6 cm
Let, AE = AF = x (The lengths of tangents drawn from an external point to a circle are equal)
CD = CE = 6 cm (Tangents from point C)
BD = BF = 8 cm (Tangents from point B)
Using Heron's formula, area of the triangle = √s (s - a)(s - b)(s - c)
where
s = 1/2 (a + b + c)
a, b and c are sides of a triangle
a = AB = x + 8
b = BC = 8 + 6 = 14
c = CA = 6 + x
s = 1/2 ( x + 8 + 14 + 6 + x)
s = 1/2 (2x + 28)
s = x + 14
Area of ΔABC = √(x + 14) ( x + 14 - x - 8)( x + 14 - 14)( x + 14 - x - 6)
= √( x + 14) × (6) × (x) × (8)
= √48x ( x + 14)
= √48 (x² + 14x) square units.....(1)
Area of ΔABC = Area of ΔAOC + Area of ΔAOB + Area of ΔBOC
= 1/2 ( x + 6) × 4 + 1/2 ( x + 8) × 4 + 1/2 (14 × 4) [Since area of a triangle = 1/2 × l × b × h]
= 2x + 12 + 2x + 16 + 28
= 4x + 56
= 4( x + 14) square units............ (2)
Equating (1) and (2)
√48 (x² + 14x) = 4(x + 14)
Squaring both sides
48(x² + 14x) = 4² (x + 14)²
48(x² + 14x) = 16 (x² + 28x + 196) [Using (a + b)² = a² + 2ab + b²]
48/16 (x² + 14x) = x² + 28x + 196
3x² + 42x = x² + 28x + 196
3x² - x² + 42x - 28x - 196 = 0
2x² + 14x - 196 = 0 (divide this equation by 2)
x² + 7x - 98 = 0
Solving by factorization method,
x² + 14x - 7x - 98 = 0
x ( x + 14) - 7 ( x + 14) = 0
( x + 14)( x - 7) = 0
x + 14 = 0 and x - 7 = 0
x = - 14 and x = 7
Since x represents length, it cannot be negative.
∴ x = 7
AB = a = x + 8 = 7 + 8 = 15 cm
AC = c = 6 + x = 6 + 7 = 13 cm
Thus, AB = 15 cm and AC = 13 cm
☛ Check: NCERT Solutions Class 10 Maths Chapter 10
Video Solution:
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC.
NCERT Solutions Class 10 Maths Chapter 10 Exercise 10.2 Question 12
Summary:
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. The lengths of side AB and AC are 15 cm and 13 cm respectively.
☛ Related Questions:
- In Figure 10.13, XY and X′ Y′ are two parallel tangents to a circle with centre O and another tangent AB with the point of contact C intersecting XY at A and X′ Y′ at B. Prove that ∠AOB = 90°.
- Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
- Prove that the parallelogram circumscribing a circle is a rhombus.
- Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
visual curriculum