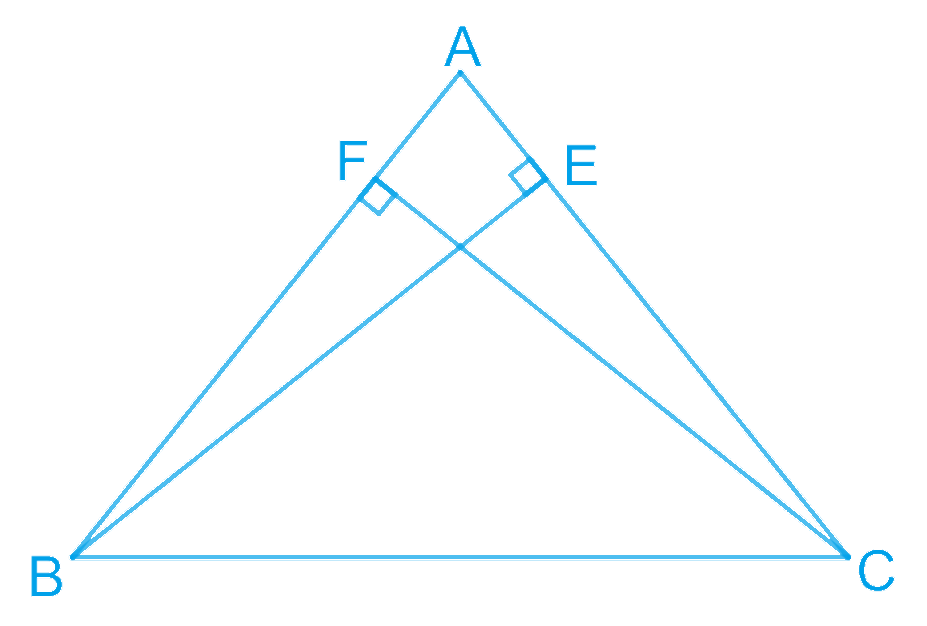
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

Solution:

Given: ΔABC is an isosceles triangle

To prove: BE = CF

In ΔAEB and ΔAFC,

∠AEB = ∠AFC (Each 90° as BE and CF are altitudes)

∠A = ∠A (Common angle)

AB = AC (Given ΔABC is an isosceles triangle)

∴ ΔAEB ≅ ΔAFC (By AAS congruence rule)

∴ BE = CF (By CPCT)

☛ Check: Class 9 Maths NCERT Solutions Chapter 7

Video Solution:

ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

NCERT Maths Solutions Class 9 Chapter 7 Exercise 7.2 Question 3

Summary:

If ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and BC respectively, then altitudes BE and CF are equal

☛ Related Questions:

• ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that(i) ΔABE ≅ ΔACF(ii) AB = AC, i.e., ABC is an isosceles triangle.
• ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ABD = ∠ACD.
• ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠BCD is a right angle.
• ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.