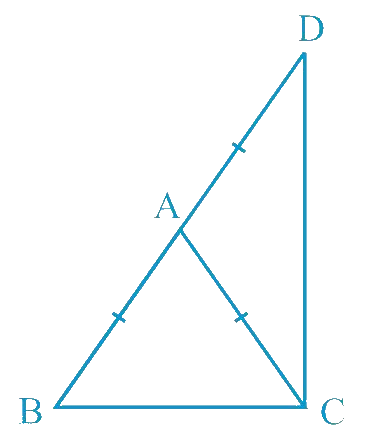
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠BCD is a right angle.
Solution:
We can use the property that angles opposite to equal sides are equal and then by the angle sum property in triangle BCD we can show the required result.

In isosceles triangle ABC,
AB = AC (Given)
∴ ∠ACB = ∠ABC (Angles opposite to equal sides of a triangle are equal)
Let ∠ACB = ∠ABC be x. ----------- (1)
In ΔACD,
AC = AD (Since, AB = AD)
∴ ∠ADC = ∠ACD (Angles opposite to equal sides of a triangle are equal)
Let ∠ADC = ∠ACD be y. ----------- (2)
Thus, ∠BCD = ∠ACB + ∠ACD = x + y ----------- (3)
In ΔBCD,
∠ABC + ∠BCD + ∠ADC = 180° (Angle sum property of a triangle)
Substituting the values we get,
x + (x + y) + y = 180° [From equation (1), (2) and (3)]
2 (x + y) = 180°
2(∠BCD) = 180° [From equation(3)]
∴ ∠BCD = 90°
☛ Check: NCERT Solutions Class 9 Maths Chapter 7
Video Solution:
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠BCD is a right angle.
NCERT Maths Solutions Class 9 Chapter 7 Exercise 7.2 Question 6
Summary:
If ΔABC is an isosceles triangle in which AB = AC, side BA is produced to D such that AD = AB. We have proved that ∠BCD is a right angle.
☛ Related Questions:
- In ΔABC,AD is the perpendicular bisector of BC.Show that ΔABC is an isosceles triangle in which AB=AC.
- ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
- ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that(i) ΔABE ≅ ΔACF(ii) AB = AC, i.e., ABC is an isosceles triangle.
- ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ABD = ∠ACD.
visual curriculum