NCERT Solutions Class 12 Maths Chapter 8 Application of Integrals
NCERT solutions for class 12 maths chapter 8 application of integrals is a continuation of the previous chapter where kids were introduced to the topic of integration and how to solve questions based on different methods. Students have learned formulas to calculate areas of various geometrical figures including triangles, rectangles, trapeziums, and circles. Such elementary formulas are fundamental in the applications of mathematics to many real-life problems. However, when it comes to calculating the areas enclosed by curves this technique fails. To determine the areas under a curve we need integral calculus. The NCERT solutions for class 12 maths chapter 8 focuses on a specific application of integrals to find the area under curves. These curves could be simple or complex like circles, parabolas, hyperbolas, etc.
In chapter 7 children have studied definite integrals as the limit of a sum and how to evaluate these integrals using the Fundamental Theorem of Calculus. NCERT solutions class 12 maths chapter 8 uses this concept to give students an easy method of calculating the area under curves. The area under the curve can be thought of as being composed of a large number of very thin vertical stripes. By integrating this region between some specific limits we can now determine the complete area required. NCERT Solutions Chapter 8 Application of Integrals uses many real-life examples to give kids a better understanding of integration. It is an amazing lesson that shows the practical implications of this topic. In this article, we will explore the variety of examples, formulas, and theories in-depth to help students build a robust mathematical foundation, download the exercises provided in the links below.
- NCERT Solutions Class 12 Maths Chapter 8 Ex 8.1
- NCERT Solutions Class 12 Maths Chapter 8 Ex 8.2
- NCERT Solutions Class 12 Maths Chapter 8 Miscellaneous Ex
NCERT Solutions for Class 12 Maths Chapter 8 PDF
Integral Calculus is related to the method of exhaustion developed by Eudoxus (440 B.C.) and Archimedes (300 B.C.). This method arose as part of the solution of problems on calculating areas of plane figures, surface areas, and volumes of solid bodies. In 1665, Newton began his work on Calculus leading to the formation of concepts as we know them today. The NCERT solutions class 12 maths chapter 8 has several tips, tricks, and interesting facts to help students break the monotony while studying as well as develop a mathematical foundation that will carry them through their careers. Given below are the exercise-wise links to the PDF files of the solutions:
☛ Download Class 12 Maths NCERT Solutions Chapter 8 Application of Integrals
NCERT Class 12 Maths Chapter 8

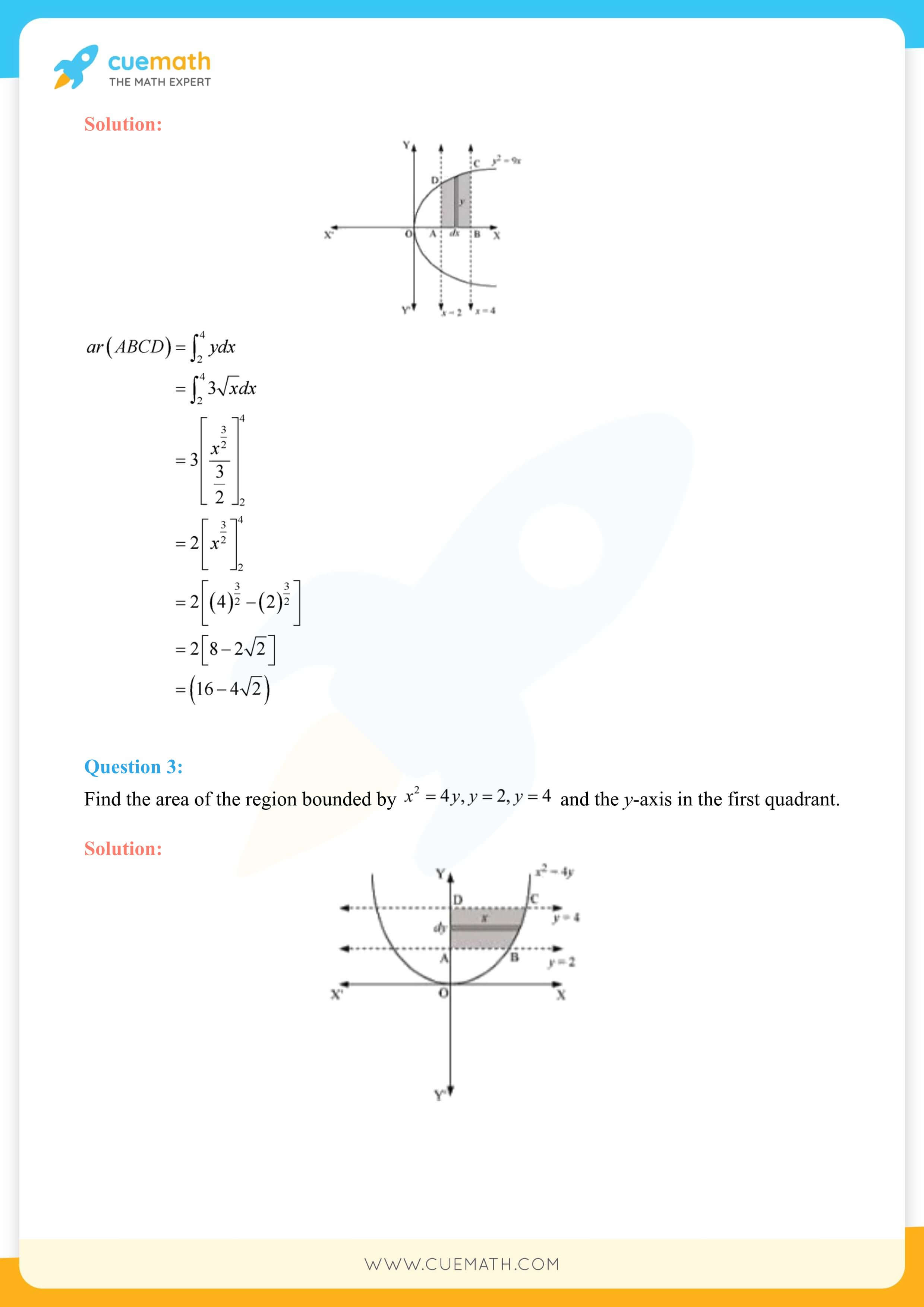







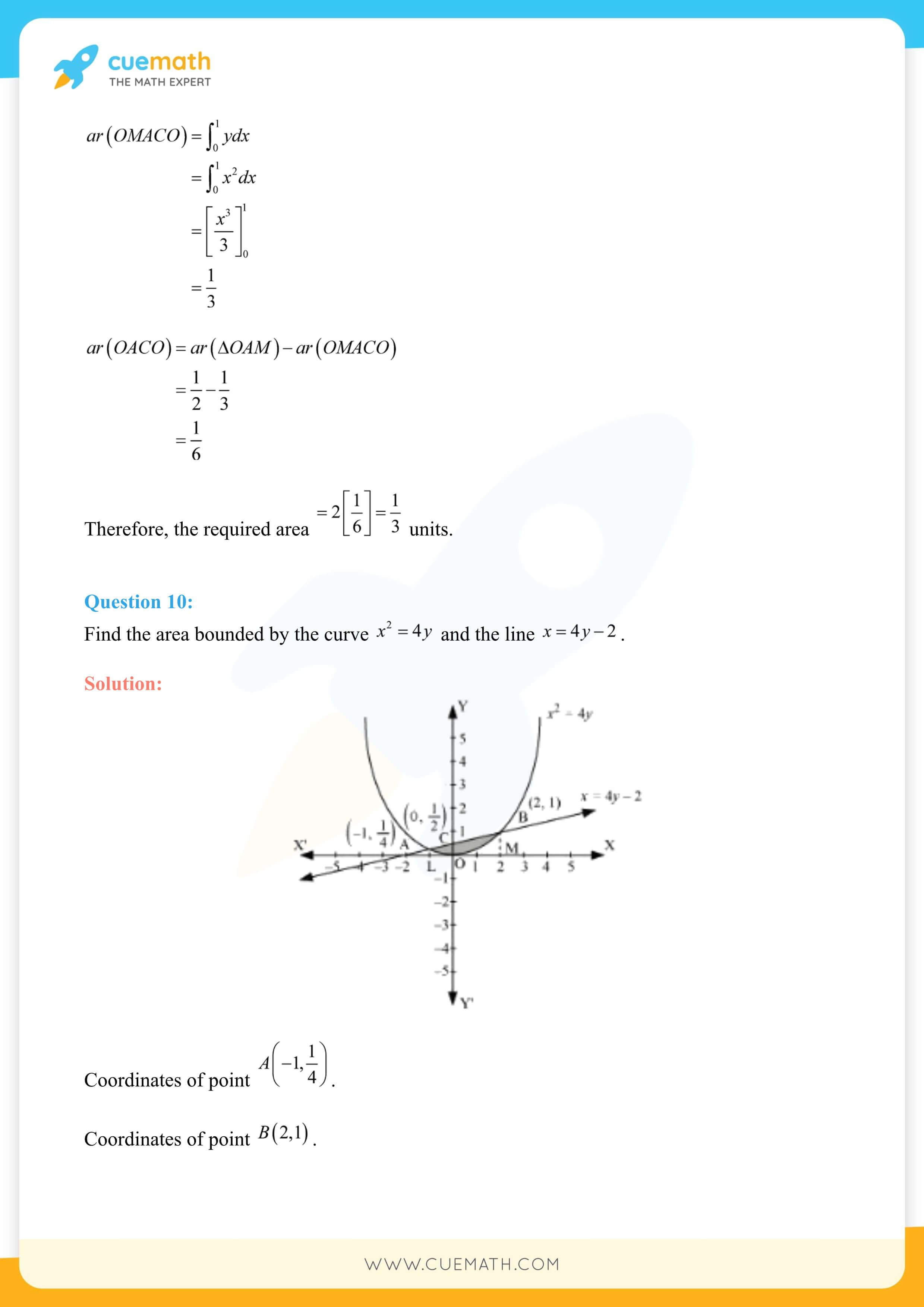



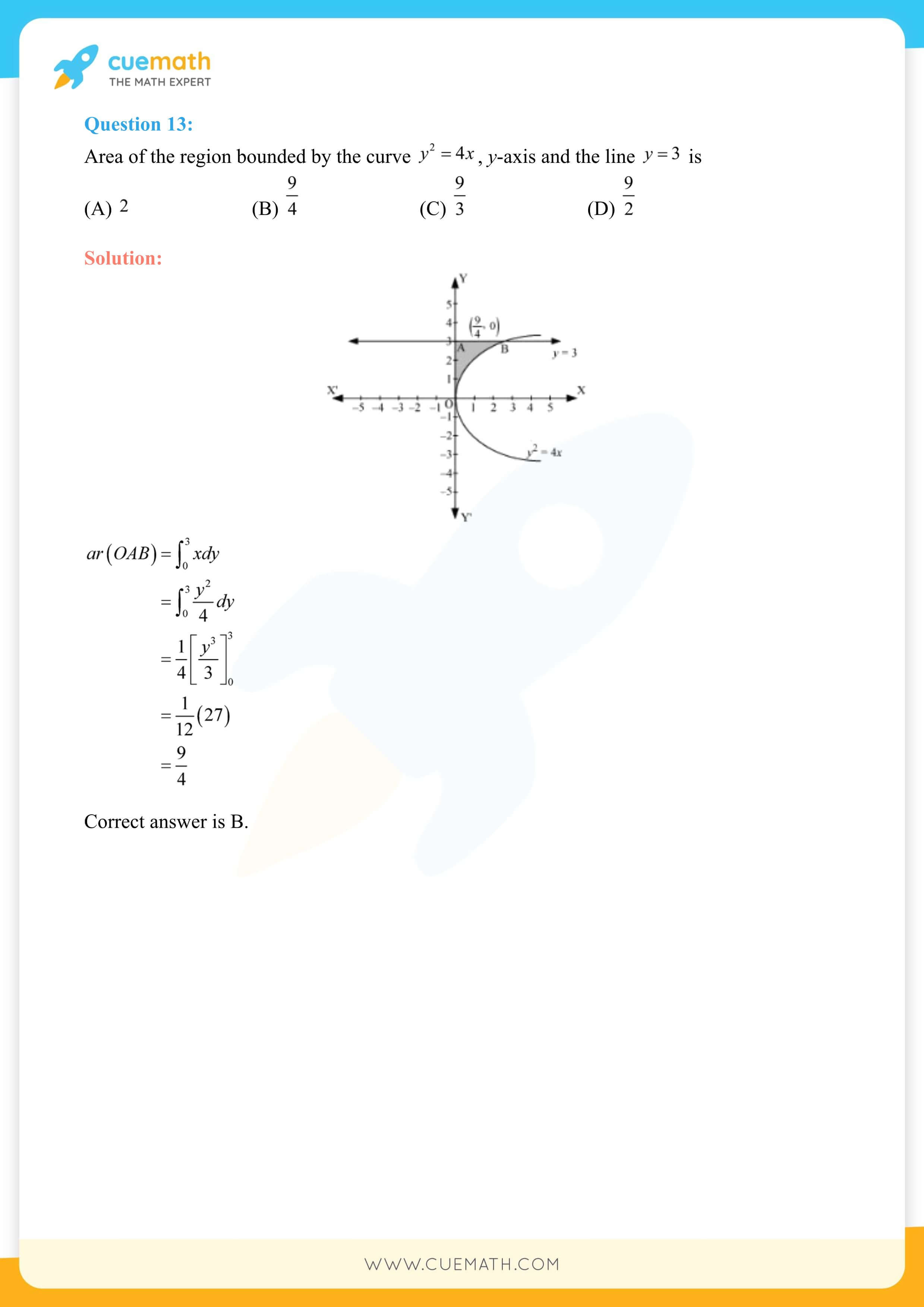





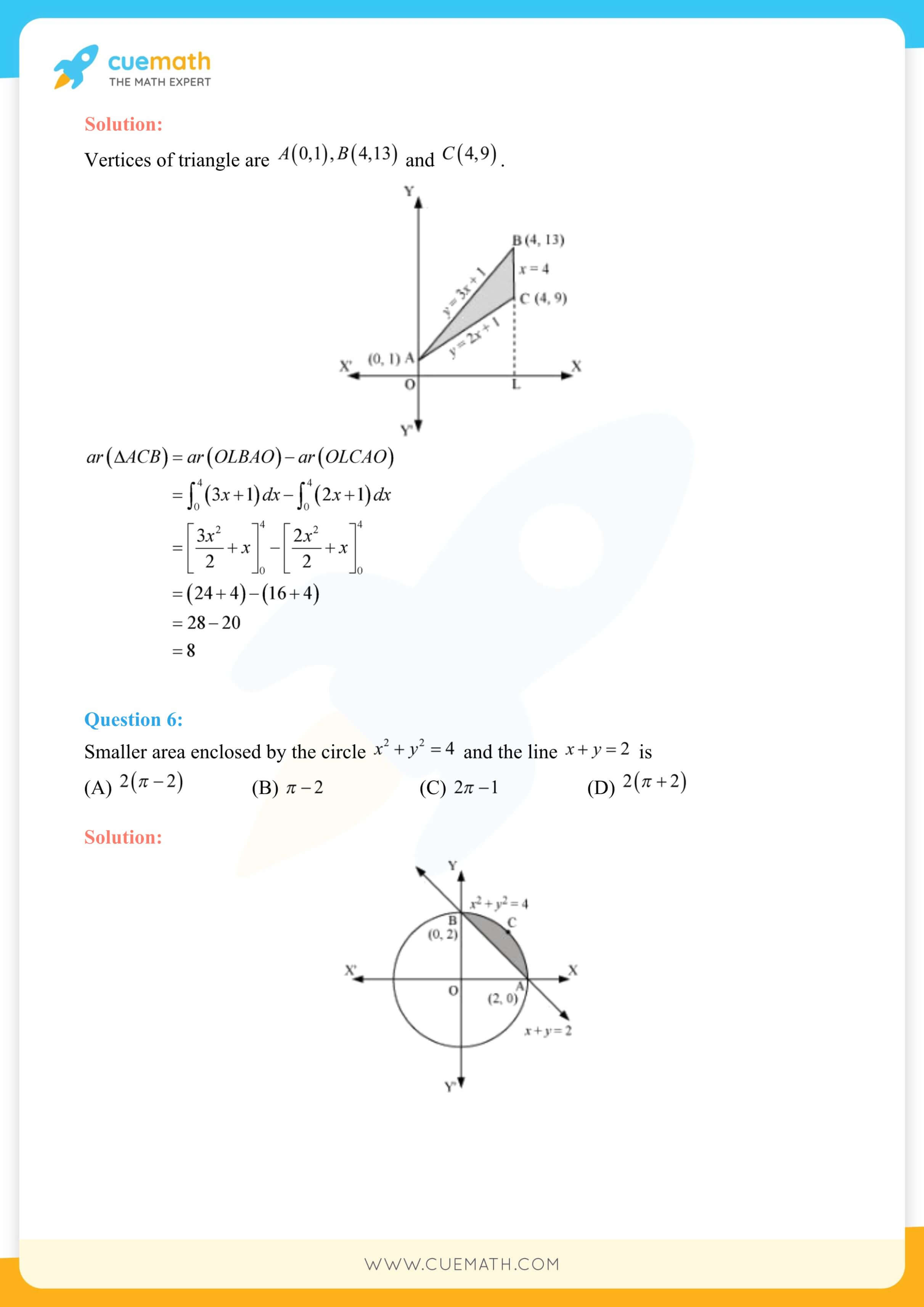


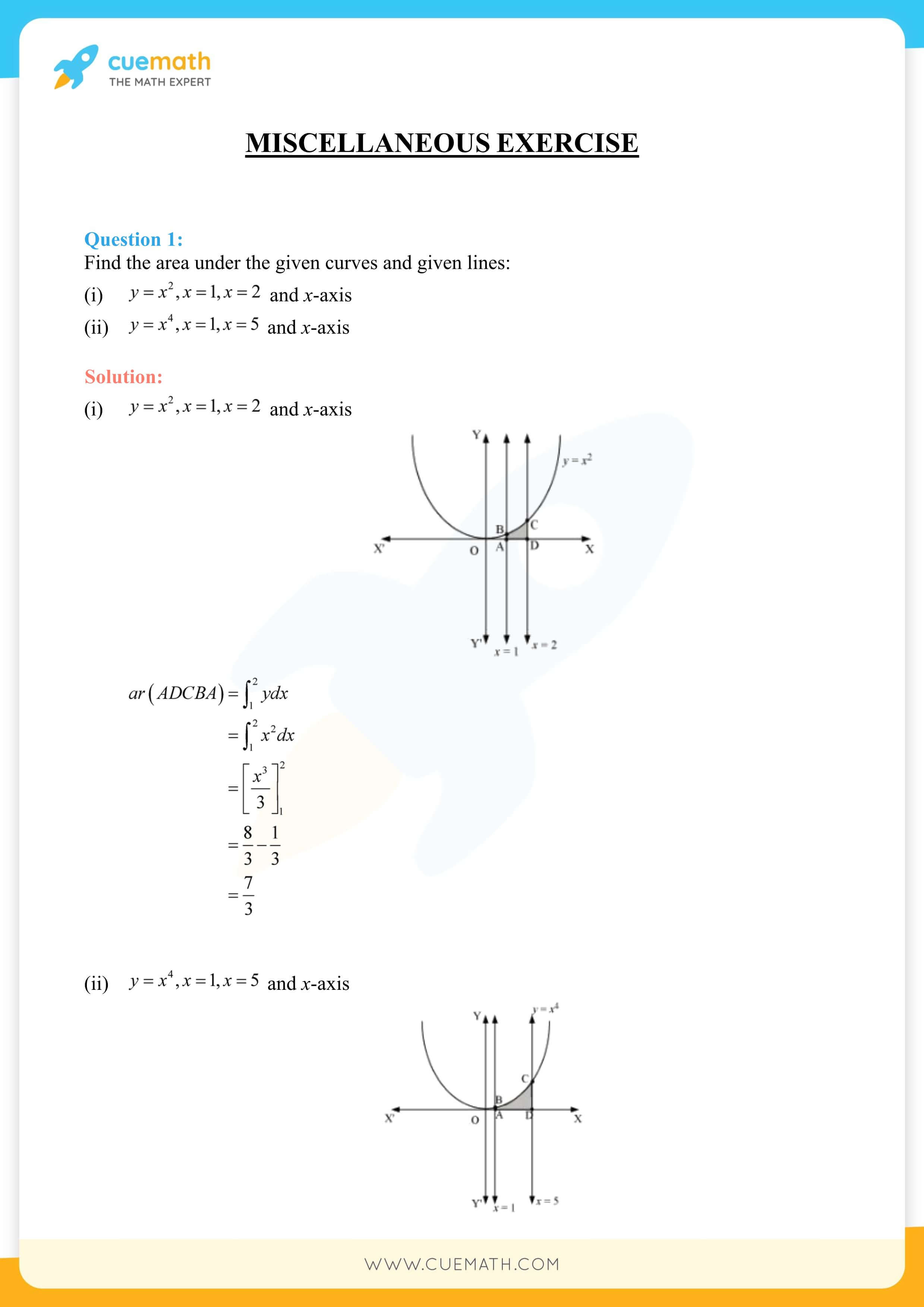
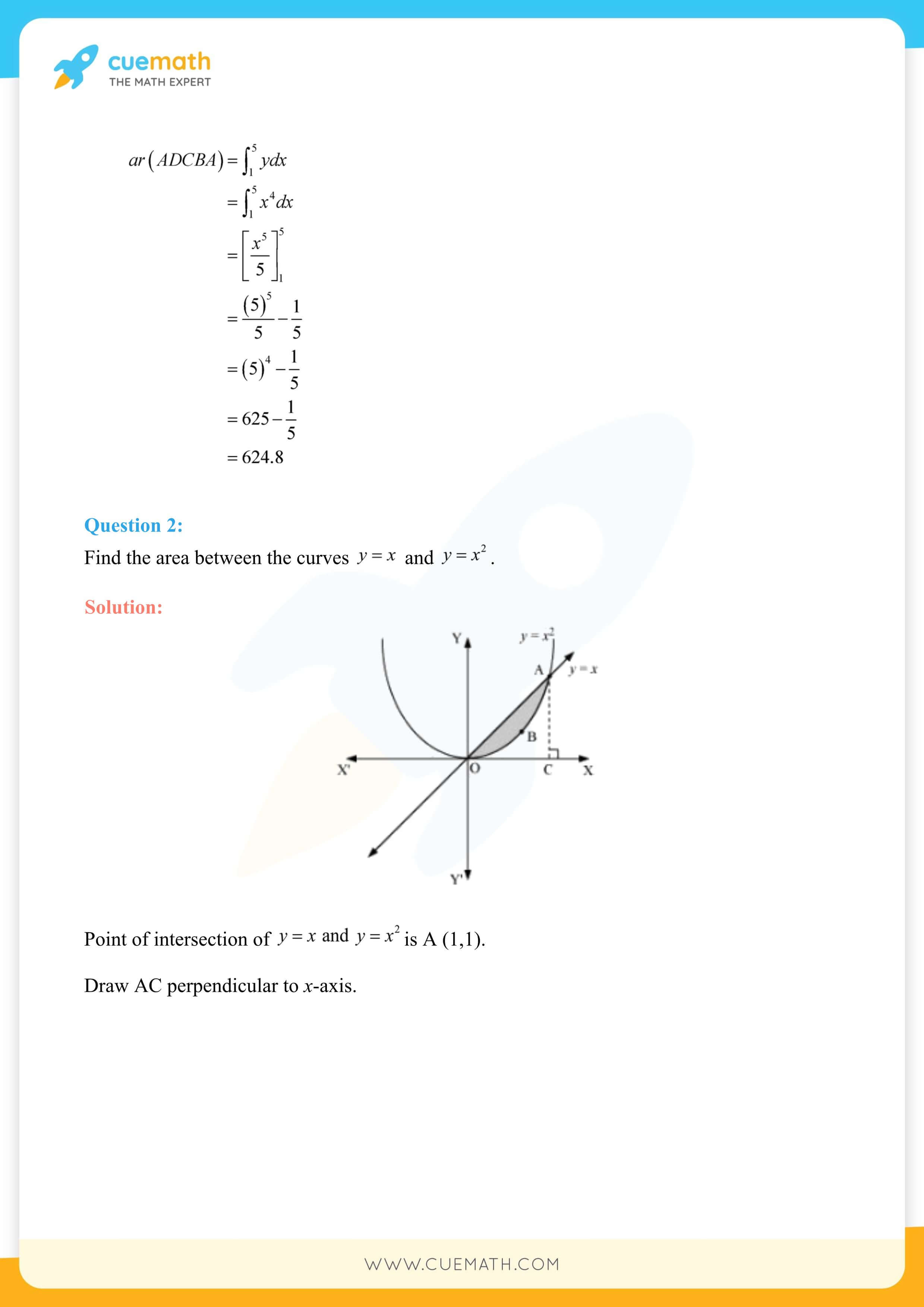


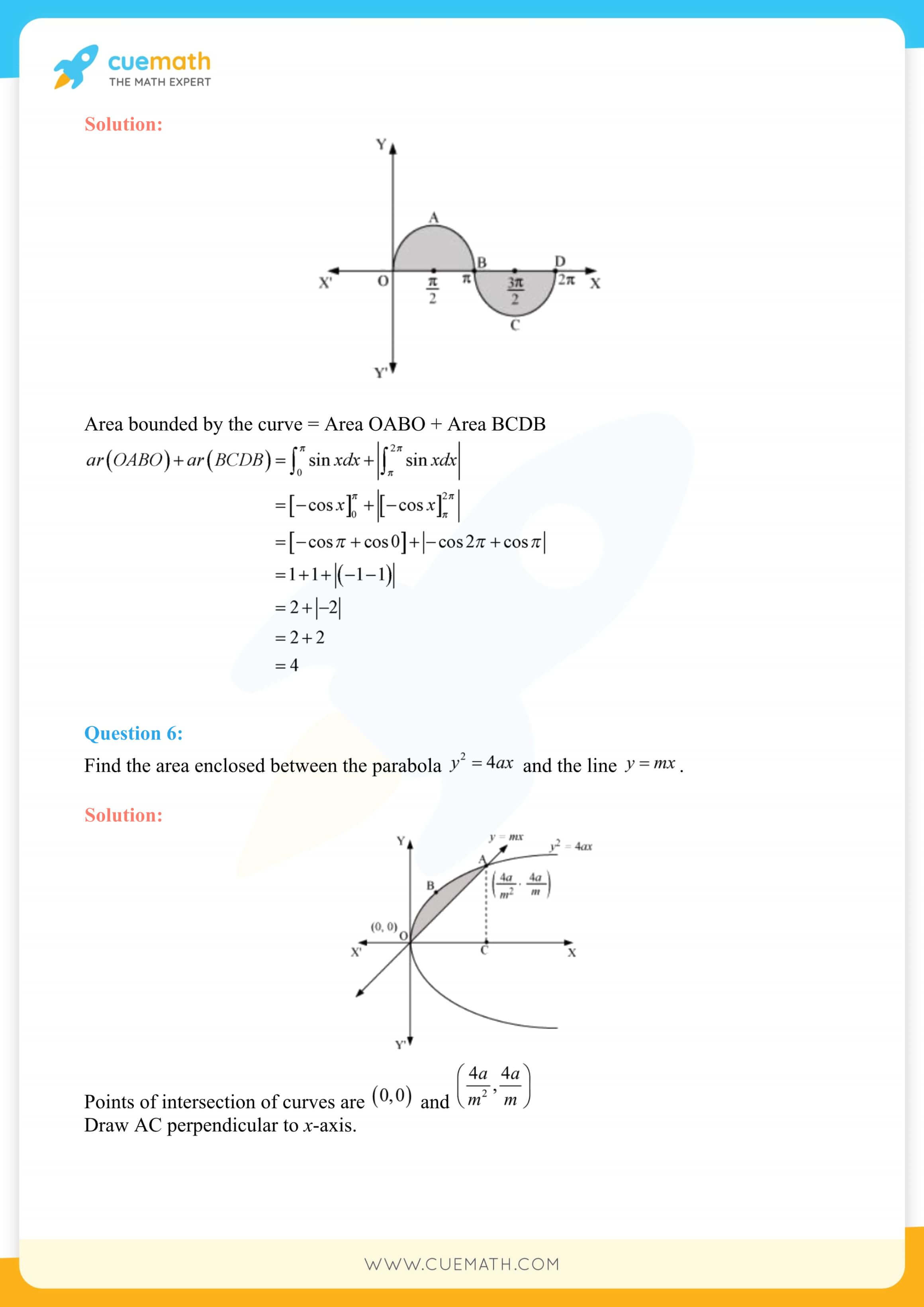
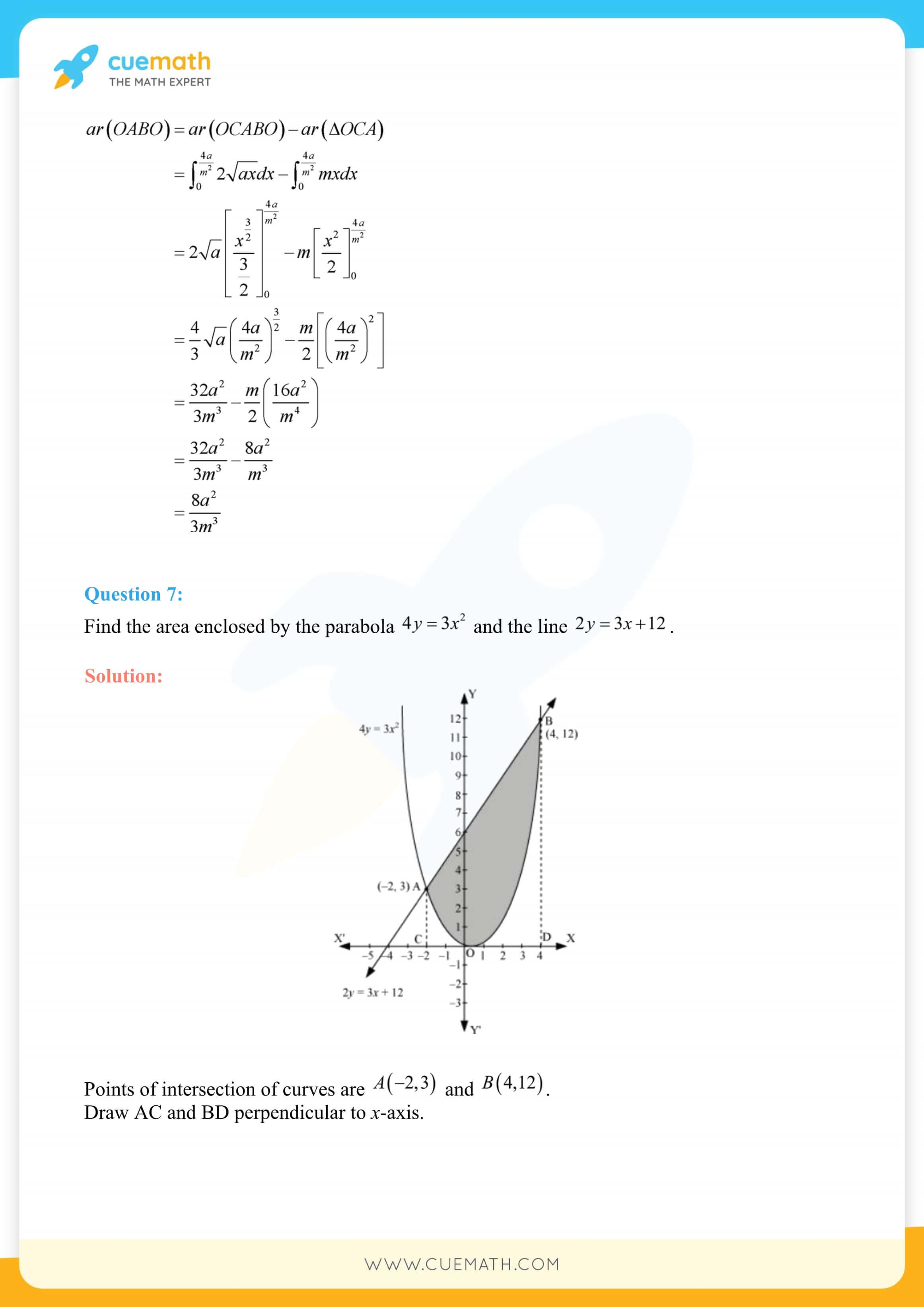








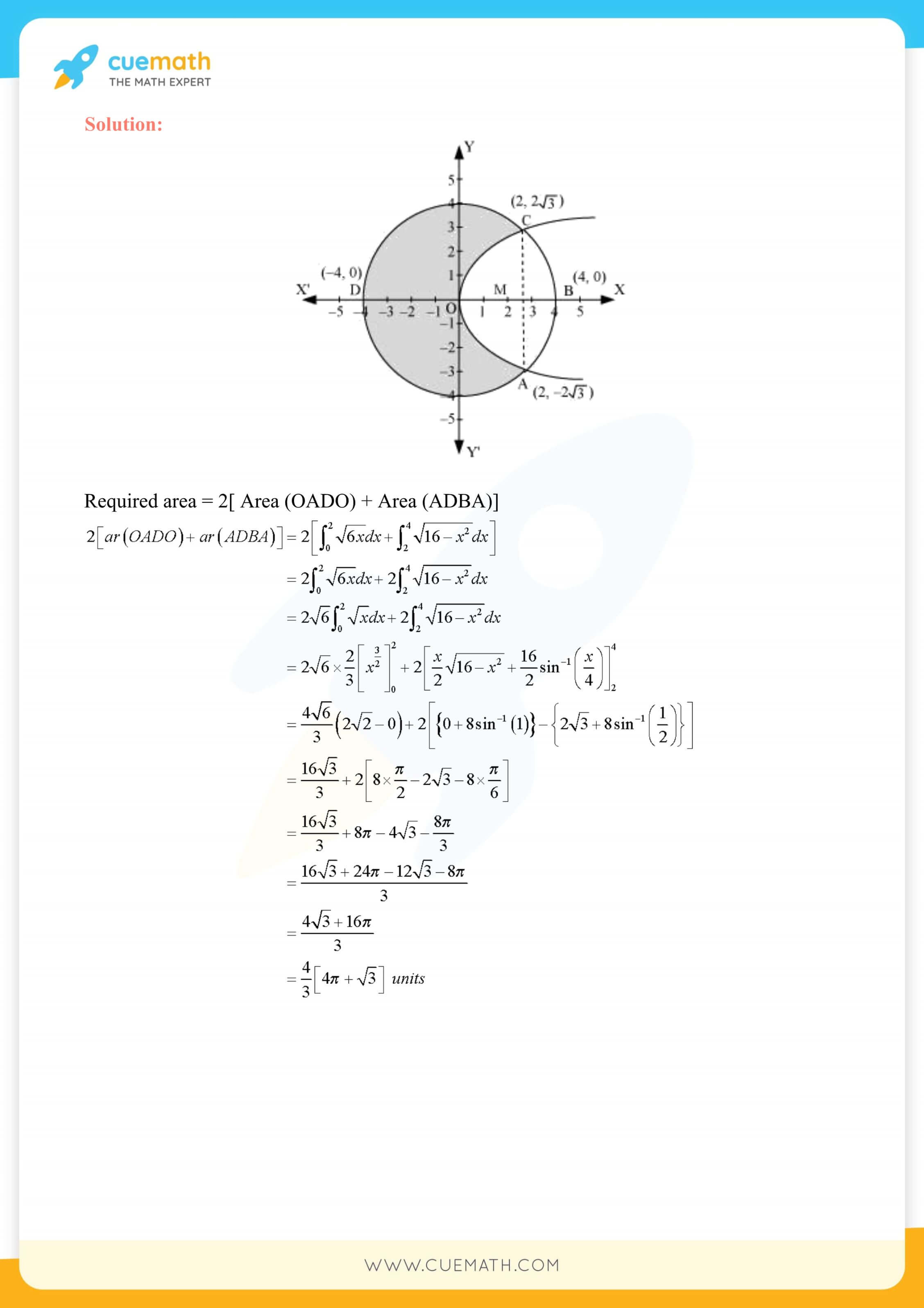


NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals
This lesson sees the use of several formulas and theorems. Additionally, there is an amalgamation of newer topics with the ones that kids have learned in the previous chapter. Integration in itself can be a tough and confusing concept if not studied in a step-wise manner. For all these reasons it is very important that students revise this lesson periodically, especially the formulas, so as to gain mastery over the subject matter. All the exercises in the NCERT Solutions Class 12 Maths Chapter 8 application of integrals are explained in detail with the help of examples and sample problems.
- Class 12 Maths Chapter 8 Ex 8.1 - 13 Questions
- Class 12 Maths Chapter 8 Ex 8.2 - 7 Questions
- Class 12 Maths Chapter 8 Miscellaneous Ex - 19 Questions
☛ Download CBSE Class 12 Maths Chapter 8 NCERT Book
Topics Covered: The topics encompassed in the Class 12 maths NCERT solutions chapter 8 are the area bound by the curve of a function, the area between two curves, and the area under simple curves.
Total Questions: Class 12 maths chapter 8 Application of Integrals has a total of 39 sums. 16 are complex questions, 8 are medium-level, and 15 are straightforward formula-based problems.
List of Formulas in NCERT Solutions for Class 12 Maths Chapter 8
NCERT solutions class 12 maths chapter 8 not only requires the use of formulas but utilizes a student’s acumen. They have to understand what the question is asking them to do and perform the operations in a phased manner. Additionally, they should break down the problem into smaller chunks so as to make it simpler and combat any confusion thus, reducing the scope of mistakes. More importantly, kids need to clearly grasp the steps followed in the procedure because these act as keys to solving a wide range of questions.
Some formulas that are frequently used in the NCERT solutions for class 12 maths chapter 8 are given below
- area of the region bounded by the curve y = f (x), x-axis and the lines x = a and x = b (b > a) : a∫b y dx = a∫bf(x) dx.
- The area of the region bounded by the curve x = φ (y), y-axis and the lines y = c, y = d : c∫d x dy = c∫d φ (y) dy.
- The area of the region enclosed between two curves y = f (x), y = g (x) and the lines x = a, x = b : b∫a[f(x) - g(x)] dx
FAQs on NCERT Solutions for Class 12 Maths Chapter 8
Why are NCERT Solutions Class 12 Maths Chapter 8 Important?
Class 12 is one of the most important grades of school life. Thus, ensuring that students have formed a mathematical foundation that will ferry them not only through this class but also help them in their college careers is equally important. The NCERT Solutions Class 12 Maths Chapter 8 gives an in-depth analysis of all exercise problems enabling kids to clear any doubts that they may have regarding that topic. Hence, children can have clarity of concepts that will remain with them throughout their lives.
Do I Need to Practice all Questions Provided in NCERT Solutions Class 12 Maths Application of Integrals?
The questions that can appear on a board examination are highly unpredictable. All the sums in the NCERT Solutions Class 12 Maths Application of Integrals have been curated by math experts so as to provide students with a 360-degree view of the chapter. Thus, practicing all problems thoroughly is a must if kids want to maximize the possibility of getting a superb score in their exams. Additionally, they should also consult previous test papers while preparing for boards.
What are the Important Topics Covered in Class 12 Maths NCERT Solutions Chapter 8?
All topics covered in the NCERT Solutions Class 12 Maths Chapter 8 are equally important. They cover the different aspects of integration and how to find the area under a curve given various conditions. Kids need to first understand the underlying concepts before attempting the exercise questions. They should also be well-versed with the previous chapter along with the listed formulas.
How Many Questions are there in NCERT Solutions Class 12 Maths Chapter 8 Application of Integrals?
There are 39 questions in the NCERT Solutions Class 12 Maths Chapter 8 Application of Integrals that have been divided into 3 exercises. Out of these, one is a miscellaneous exercise that has complicated sums meant to build a student’s critical thinking and analytical abilities. All problems are important thus, kids should not skip any and must revise the exercises at least twice before appearing for any exam.
How CBSE Students can utilize NCERT Solutions Class 12 Maths Chapter 8 effectively?
The first step to utilizing the NCERT Solutions Class 12 Maths Chapter 8 effectively is to have a strong knowledge of integration that can be developed by studying the previous chapter. The next step is to go through the theory that is highlighted in each section of chapter 8. Finally, kids need to apply the formulas and techniques learned along with cross-referencing their answers with these solutions.
Why Should I Practice NCERT Solutions Class 12 Maths Application of Integrals Chapter 8?
Practice makes a man perfect his art. The NCERT Solutions Class 12 Maths Application of Integrals Chapter 8 can prove to be a complicated topic because it uses several formulas as well as tricky concepts. In order to, develop a firm understanding of each topic students need to constantly gauge their mathematical abilities by practicing these questions. With regular revision and due diligence, kids are sure to ace any exam be it boards or competitive.
visual curriculum