Square Root of 150

The square root of 150 is expressed as √150 in the radical form and as (150)^½ or (150)^0.5 in the exponent form. The square root of 150 rounded up to 9 decimal places is 12.247448714. It is the positive solution of the equation x² = 150. We can express the square root of 150 in its lowest radical form as 5 √6.

• Square Root of 150: 12.24744871391589
• Square Root of 150 in exponential form: (150)^½ or (150)^0.5
• Square Root of 150 in radical form: √150 or 5 √6

• The square root of 150 = 150^½ = √150
• √150 = √(a × a) which is √150 = √(12.247 × 12.247) or √(-12.247 × -12.247) ⇒ √150 = ±12.247
• We know that on prime factorization, 150 = 2 × 3 × 5 × 5. Thus, in the simplest radical form √150= √(2 × 3 × 5 × 5) = 5√6

Irrational numbers are the real numbers that cannot be expressed as the ratio of two integers p/q. √150 = 12.24744871391589 and hence, the square root of 150 is an irrational number where the numbers after the decimal point go up to infinity.

The square root of 150 or any number can be calculated in many ways. Two of them are the approximation method and the long division method.

Square Root of 150 by Approximation Method

• Take two perfect square numbers which are just smaller than 150 and just greater than 150. √144 < √150 < √169
• 12 < √150 < 13
• Divide 150 by 12 or 13.
• Let us divide by 13 ⇒ 150 ÷ 13 = 11.53
• Find the average of 11.53 and 13.
• (11.53 + 13) / 2 = 24.53 ÷ 2 = 12.265
• √150 ≈ 12.26

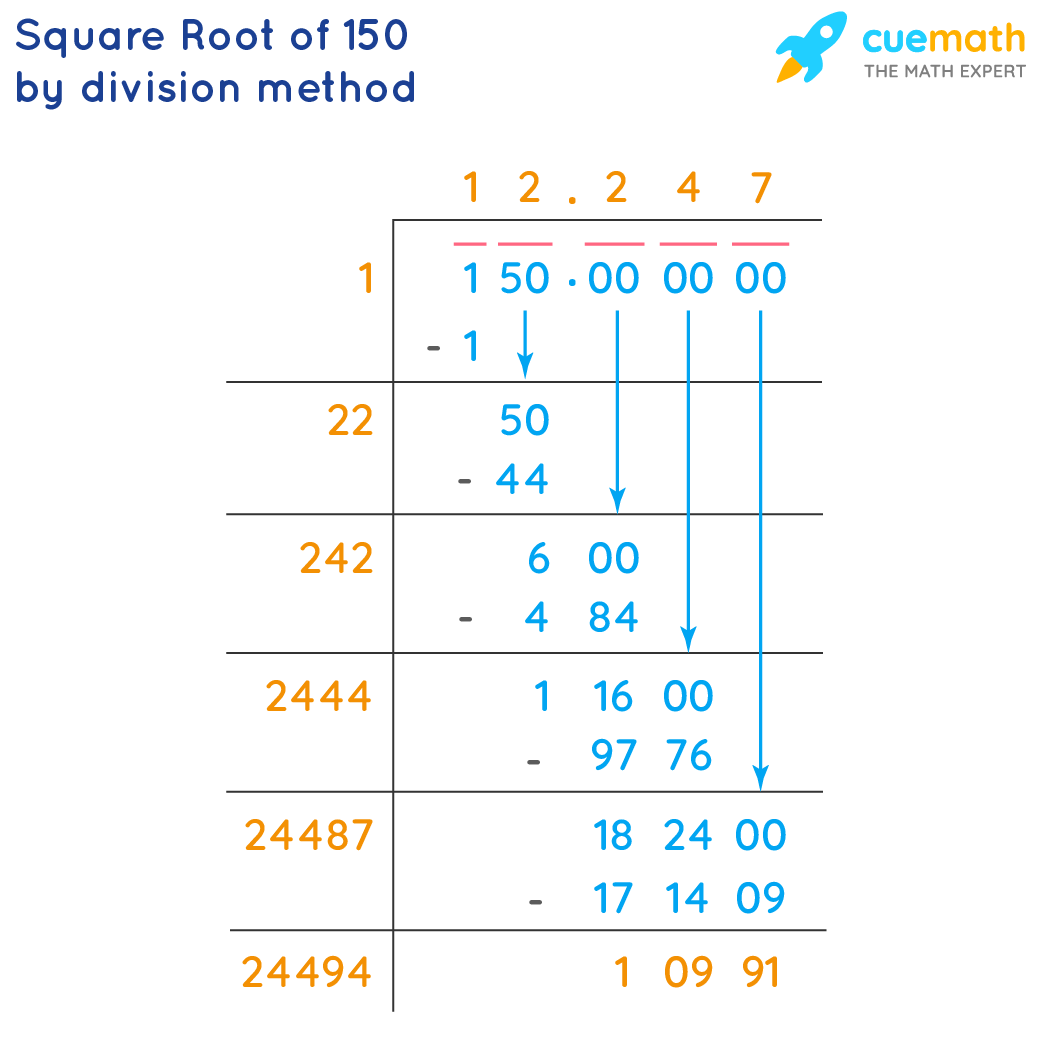
Square Root of 150 by the Long Division Method

The long division method helps us to find a more accurate value of the square root of any number. The following are the steps to evaluate the square root of 150 by the long division method.

• Step 1: Write 150.000000. Take the number in pairs from the right. We will have 50 as one pair and 1 stand-alone. Now divide 1 by a number such that (number × number) gives ≤ 1.
• Obtain quotient = 1 and remainder = 0. Double the quotient. We get 2. We have 20 as our new divisor. Bring down 50 for division.
• Step 2: Find a number x such that (20 + x) × x gives the product ≤ 50. We find 22 × 2 = 44. Subtract this from 50 and get the remainder as 6. Bring down two zeros. 600 is our new dividend.
• 12 is our quotient. Double it. 240 is our new divisor. Find a number z such that (240 + z) × z gives 600 or less than that. We will consider 2 as the number z. 242 × 2 = 484
• Step 3: Quotient is 12.2 and the remainder is 116. Bring down the next pair of zeros. 11600 becomes the new dividend.
• Double the quotient. 122 × 2 = 244. Have 2440 in the place of the new divisor. Find a number such that (2440 + that number) × number ≤ 11600.
• We find 2444 × 4 = 9776. Subtract this from 11600 and get the remainder 1824. Bring down 00.
• Repeat the steps until we approximate the square root to 3 decimal places. √150 = 12.247

Explore square roots using illustrations and interactive examples:

• Square root of 170
• Square root of 160
• Square root of 120
• Square root of 180
• Square root of 120

Did you know that on prime factorization of 150, we get: 2 × 3 × 5 × 5. Thus, 2 and 3 are the factors that don't have a pair. So 6 is the least number to be multiplied by 150 to make it a perfect square. 6 is the least number to be divided with 150 to make a perfect square. Can you find those perfect squares and their square roots?

• The square root of 150 is 12.247 approximated to 3 decimal places.
• The simplified form of √150 in its radical form is 5√6.
• √150 is an irrational number. It is a real number with 2 roots, i.e. √150 = ±12.247

What is the Value of the Square Root of 150?

The square root of 150 is 12.24744.

Why is the Square Root of 150 an Irrational Number?

Upon prime factorizing 150 i.e. 2¹ × 3¹ × 5², 2 is in odd power. Therefore, the square root of 150 is irrational.

What is the Square Root of -150?

The square root of -150 is an imaginary number. It can be written as √-150 = √-1 × √150 = i √150 = 12.247i, where i = √-1 and it is called the imaginary unit.

What is the Square of the Square Root of 150?

The square of the square root of 150 is the number 150 itself i.e. (√150)² = (150)^2/2 = 150.

What is the Square Root of 150 in Simplest Radical Form?

We need to express 150 as the product of its prime factors i.e. 150 = 2 × 3 × 5 × 5. Therefore, √150 = √(2 × 3 × 5 × 5) = 5 √6. Thus, the square root of 150 in the lowest radical form is 5 √6.

Is the number 150 a Perfect Square?

The prime factorization of 150 = 2¹ × 3¹ × 5². Here, the prime factor 2 is not in the pair. Therefore, 150 is not a perfect square.