Sum of Squares of n Natural Numbers

The sum of squares of n natural numbers can be calculated using the formula [n(n+1)(2n+1)] / 6. Let n be a natural number. We evaluate the sum of the squares in statistics to find the variation in the data. There are different techniques to find the sum of squares of given numbers.

In this article, we will discuss the formula to calculate the sum of squares of n natural numbers and prove it using the principle of mathematical induction. We will also discuss the formula to find the sum of squares of even and odd natural numbers and the sum of squares in geometry. We will also solve a few examples for a better understanding of the concept.

1.	What is Sum of Squares of n Natural Numbers?
2.	Sum of Squares of n Natural Numbers Formula
3.	Sum of Squares of Two and Three numbers
4.	Sum of Squares of Natural Numbers Proof
5.	Sum of Squares of Even Natural Numbers
6.	Sum of Squares of Odd Natural Numbers
7.	Sum of Squares in Geometry
8.	FAQs on Sum of Squares

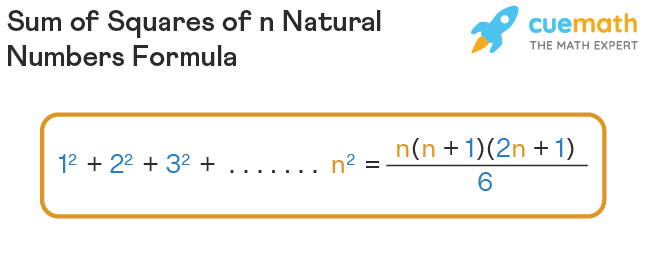
Let us first recall the meaning of natural numbers. The natural numbers are the counting numbers from 1 to infinity. If we consider n consecutive natural numbers, then finding the sum of the squares of these numbers is represented as Σ_{i = 1} ⁿ i². We can find the sum of squares of the first n natural numbers using the formula, SUM = 1² + 2² + 3² + ... + n² = [n(n+1)(2n+1)] / 6. We can prove this formula using the principle of mathematical induction.

☛ Also Check: Sum of Squares

Let's go through the formulas of finding the sum of squares of even and odd natural numbers in the next section.

Here are the formulas for finding the sum of squares of n natural numbers, the sum of squares of first n even numbers, and the sum of squares of first n odd numbers:

Sum of squares of first n natural numbers	[n(n+1)(2n+1)] / 6
Sum of squares of first n even numbers	[2n(n + 1)(2n + 1)] / 3
Sum of squares of first n odd numbers	[n(2n+1)(2n-1)] / 3

For small numbers, we can directly find the squares and add them, but for larger numbers, we need to know the identity to use to ease our calculations. Let a and b be the 2 numbers. Their squares are a² and b². The sum of their squares is a² + b². We could obtain a formula using the known algebraic identity (a+b)² = a² + b² + 2ab. From this we conclude that a² + b² = (a + b)² - 2ab.

Let a, b, c be the 3 numbers for which we are supposed to find the sum of squares. The sum of their squares is a² + b² + c². Using the known algebraic identity (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca, we can evaluate that a² + b² + c² = (a + b + c)² - 2ab -2bc -2ca.

Let us learn to evaluate the sum of squares for larger sums. We can readily use the formula available to find the sum, however, it is essential to learn the derivation of the sum of squares of n natural numbers formula: Σn² = [n(n+1)(2n+1)] / 6. It is easy to apply the formula when the value of n is known. Let us prove this formula using the principle of mathematical induction.

Let P(n): 1² + 2² + 3² + ... + n² = [n(n+1)(2n+1)] / 6

Consider P(1). LHS = 1² = 1, RHS = [1(1+1)(2(1)+1)] / 6 = (1 × 2 × 3) / 6 = 6/6 = 1. So, LHS = RHS. Therefore, P(1) is true.

Assume P(k) is true, i.e., 1² + 2² + 3² + ... + k² = [k(k+1)(2k+1)] / 6 holds true. ---- (1)

Now we will prove that P(k+1) is true, that is, we need to prove that 1² + 2² + 3² + ... + (k+1)² = [(k+1)(k+2)(2k+3)] / 6 is true.

Consider LHS = 1² + 2² + 3² + ... + (k+1)²

= 1² + 2² + 3² + ... + k² + (k+1)²

= [k(k+1)(2k+1)] / 6 + (k+1)² --- [Using (1)]

= (k+1)/6 × [k(2k+1) + 6(k+1)]

= (k+1)/6 × [2k² + k + 6k + 6]

= (k+1)/6 × (2k² + 7k + 6)

= (k+1)/6 × (2k² + 4k + 3k + 6)

= (k+1)/6 × [2k(k + 2) + 3(k + 2)]

= = (k+1)/6 × (2k+3)(k + 2)

= [(k+1)(k+2)(2k+3)] / 6

= RHS

So, P(k+1) is true.

Thus, we can say that P(n) is true for all natural numbers n. So, we have 1² + 2² + 3² + ... + n² = [n(n+1)(2n+1)] / 6. Hence, we have derived the formula for the sum of squares of n natural numbers.

Alternate Proof:

n³ - (n-1)³ = (n- n+1)(n² +n(n-1)+ (n-1)²)

n³ - (n-1)³ = 1(n² +n²-n+ n² + 1 - 2n)

= 3n² - 3n + 1

n³ - (n-1)³ = 3n²- 3n + 1 ----------> (1)

(n-1)³ - (n-2)³ = 3 (n-1)² - 3(n-1) +1----------> (2)

(n-2)³ - (n-3)³ = 3 (n-2)² - 3(n-2) +1----------> (3)

...................

2³ - 1³ = 3 (2)² - 3(2) +1

1³- 0³ = 3 (1)² - 3(1) +1---------->(last step)

(1) + (2) + (3) +............+ (the last step) ⇒ By adding all the above steps, we get, n³ - 0³ = 3 Σ n² - 3Σ n + n

n³ = 3 Σ n² - [3n(n+1)/2]+ n [ since Σ n = n(n+1)/2 (sum of n natural numbers)]

3 Σ n² = n³ + [3n(n+1)/2] - n

3 Σ n² = n[n² + 3(n+1)/2 - 1] --- (Taking n as common from RHS)

Σ n² = (n/3)( n² + (3n+3)/2 -1)

= (n/6) (2n²+ 3n + 1)

Factorizing the quadratic expression,

Σ n² = 1² + 2² + 3² + ... + n² = [n(n+1)(2n+1)] / 6

The even numbers are denoted by 2n, where n is the natural number. The summation of the squares of first n even numbers is given as 2² + 4²+ 6²+ 8² + 10² + 12² + ........(2n)². We are required to identify n and apply it in the known formula [2n(n + 1)(2n + 1)] / 3. Let us derive the formula from the already learned formulas. When n takes the value from 1 to ∞, we evaluate Σ(2n)² as, Σ(2² . n²) as follows.

Σ(2n)² = 2².1² + 2².2² + 2².3² + 2².4² +…+ 2².n²

Σ(2n)² = 2²(1² + 2² + 3² + 4² … + n²)

Σ(2n)² = 4 [n(n+1)(2n+1)] / 6 (Formula for sum of squares of n natural numbers)

Thus Σ(2n)² = [2n(n + 1)(2n + 1)] / 3

The odd numbers are denoted by (2n-1), where n is the natural number. The sum of the squares of the first n odd natural numbers is given by 1² + 3² + 5² + … + (2n – 1)². Identify n and apply in the known formula [n(2n+1)(2n-1)] / 3. Let us get the proof as follows:

Σ(2n-1)² = 1² + 2² + 3² + … + (2n – 1)² + (2n)² – [2 ² + 4² + 6² + … + (2n)²]

Σ(2n-1)² = (the sum of all the consecutive integers from 1 to 2n) - (the sum of the squares of the even numbers)

Σ(2n-1)² = [1² + 2² + 3² + … + (2n – 1)² + (2n)² ] – [2²+ 4² + 6²+ … + (2n)²]

On applying the formula for the addition of squares of 2n natural numbers and of n even natural numbers, we get;

Σ(2n-1)² = [2n(2n+1)(4n+1)] / 6 - [2n(n + 1)(2n + 1)] / 3

= [n(2n+1)(4n+1)] / 3 - [2n(n + 1)(2n + 1)] / 3

Taking out the common terms, we get;

Σ(2n-1)² = (n/3) (2n+1) [4n+1 - 2(n+1)]

= (n/3) (2n+1) (4n+1-2n-2)

= [n(2n+1)(2n-1)] / 3

Σ(2n-1)² = [n(2n+1)(2n-1)] / 3

As we know, in a right-angled triangle, the sum of the squares of the perpendicular and the base is equal to the square of the hypotenuse. This result is known as the Pythagoras theorem. So, we have the sum of squares in geometry given by,

Base² + Perpendicular² = Hypotenuse²

Important Notes on Sum of Squares of n Natural Numbers

• The sum of squares of first n natural numbers is, Σ n² = 1² + 2² + 3² + ... + n² = [n(n+1)(2n+1)] / 6
• The sum of squares of even and odd natural numbers is given by,
  • Σ(2n-1)² = [n(2n+1)(2n-1)] / 3
  • Σ(2n)² = [2n(n + 1)(2n + 1)] / 3
• We can derive the formula for the sum of squares of n natural numbers using the principle of mathematical induction.

☛Related Articles:

• Sum of Arithmetic Sequence
• Sum of a GP
• Perfect Squares Formula
• Sum of Squares Calculator

 

What is the Sum of Squares of n Natural Numbers?

We can calculate the sum of squares of n natural numbers using the formula, Σ n² = 1² + 2² + 3² + ... + n² = [n(n+1)(2n+1)] / 6. This can be verified by the principle of mathematical induction.

What is the Sum of Square Numbers in Algebra?

The sum of square numbers is given as a²+ b²+ c² +..... up to infinity. For the sum of squares of 2 numbers and 3 numbers in algebra, we use the known algebraic identities; Some of the formulas are:

• a² + b² = (a + b)² - 2ab
• a² + b² + c² = (a + b + c)² - 2ab -2bc -2ca

How do you Calculate the Sum of Squares of Natural Numbers?

• The sum of the squares of n natural numbers is calculated using the formula [n(n+1)(2n+1)]/6.
• The sum of the squares of n odd natural numbers is calculated using the formula [n(2n+1)(2n-1)] / 3.
• The sum of the squares of n even natural numbers is calculated using the formula [2n(n + 1)(2n + 1)] / 3.

What is the Sum of Squares of 100 Natural numbers from 1 to 100?

To calculate the sum of the squares of the numbers from 1 to 100, we apply the sum of squares of first n natural numbers formula, i.e., 1² + 2² + 3² + 4² + 5² + 6²+ ....n² = [n(n+1)(2n+1)]/6, so, 1² + 2² + 3² + 4² + 5² + 6²+ .....100² = [100(101)(201)]/6 = 338,350.

What is the Sum of Squares of Even Natural Numbers?

The sum of squares of even natural numbers is given by Σ(2n)² = [2n(n + 1)(2n + 1)] / 3.

What is the Sum of Squares in Geometry?

We have the sum of squares in a right triangle given by Base² + Perpendicular² = Hypotenuse². This follows by Pythagoras theorem.

What is the Sum of Squares of Odd Natural Numbers?

The sum of squares of odd natural numbers is given by Σ(2n-1)² = [n(2n+1)(2n-1)] / 3.