A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.

a2+b2+c2 Formula

The a2 + b2 + c2 formula is used to find the sum of squares of three numbers without actually calculating the squares. It says a2 + b2 + c2 = (a + b + c)2 - 2ab - 2bc - 2ca.

a2 + b2 + c2 formula is one of the major algebraic identities. To derive the expansion of a2 + b2 + c2 formula evaluate the (a + b + c)2 formula. Let us learn more about the a2 + b2 + c2 formula along with solved examples.

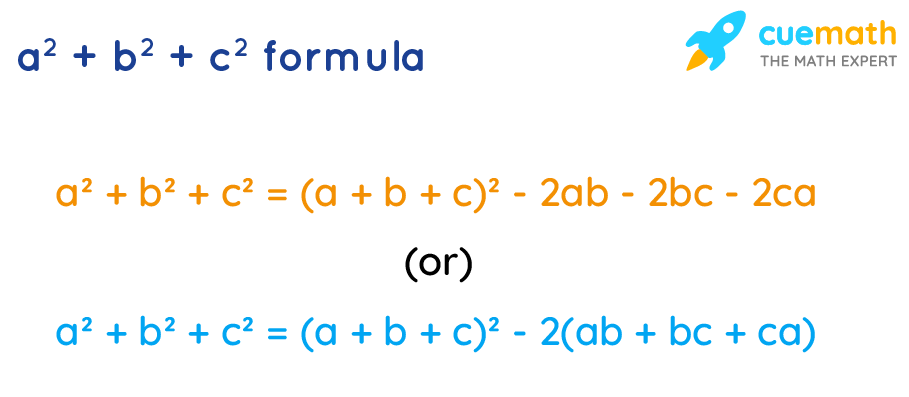
a square plus b square plus c square formula says a plus b plus c whole squared minus 2 a b minus 2 b c minus 2 c a.

What is a^2 + b^2 + c^2 Formula?

a2 + b2 + c2 formula says (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca. It is derived from (a + b + c)2 formula as follows.

We just read that by multiplying (a + b + c) by itself we can easily derive the a2 + b2 + c2 formula.
(a + b + c)2 = (a + b + c)(a + b + c)
(a + b + c)2 = a2 + ab + ac + ab + b2 + bc + ca + bc + c2
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

On subtracting 2ab + 2bc + 2ca from both sides of the above formula, the a2 + b2 + c2 formula is:

a2 + b2 + c2 = (a + b + c)2 - 2 (ab + bc + ca)

(or)

a2 + b2 + c2 = (a + b + c)2 - 2ab - 2bc - 2ca

a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ca)

This is the expansion of a2 + b2 + c2 formula.

Similarly, we can also express a2 + b2 + c2 formula in one of the following ways:

  • a2 + b2 + c2 = (a - b - c)2 + 2ab + 2ac - 2bc
  • a2 + b2 + c2 = (a - b + c)2 + 2ab - 2ac + 2bc
  • a2 + b2 + c2 = (a + b - c)2 - 2ab + 2ac + 2bc, etc.

Let us see how to use the a2 + b2 + c2 formula in the following section.

Want to find complex math solutions within seconds?
Use our free online calculator to solve challenging questions. With Cuemath, find solutions in simple and easy steps.

Book a Free Trial Class

Examples on a2 + b2 + c2 Formula

Let us take a look at a few examples to better understand the formula of a squared plus b squared plus c squared.

Example 1: Find the value of a2 + b2 + c2 if a + b + c = 10 and ab + bc + ca = -2.

Solution:

To find: a2 + b2 + c2
Given that:
a + b + c = 10
ab + bc + ca = -2
Using the a2 + b2 + c2 formula,
a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ca)
a2 + b2 + c2 = (10)2 - 2(-2) = 100 + 4 = 104

Answer: ∴ a2 + b2 + c2 = 104.

Example 2: Find the value of a2 + b2 + c2 if a + b + c = -3, 1/a + 1/b + 1/c = -2 and abc = 3.

Solution:

To find: a2 + b2 + c2
Given that:
a + b + c = -3 ... (1)
1/a + 1/b + 1/c = -2 ... (2)
abc = 3 ... (3)
Multiplying (2) and (3),
abc(1/a + 1/b + 1/c) = (3)(−2)
bc + ca + ab = −6
Using the a2 + b2 + c2 formula,
a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ca)
a2 + b2 + c2 = (-3)2 - 2(-6) = 9 + 12 = 21

Answer: ∴ a2 + b2 + c2 = 21.

Example 3: Find the value of a2 + b2 + c2 if a + b + c = 20 and ab + bc + ca = 100.

Solution:

To find: a2 + b2 + c2
Given that:
a + b + c = 20
ab + bc + ca = 100
Using the a2 + b2 + c2 formula,
a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ca)
a2 + b2 + c2 = (20)2 - 2(100) = 400 - 200 = 200

Answer: ∴ a2 + b2 + c2 = 200.

FAQs on a2 + b2 + c2 Formulas

What is the Expansion of a^2 + b^2 + c^2 Formula?

a2 + b2 + c2 formula is read as a square plus b square plus c square. Its expansion is a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ca).

How to Derive a Square Plus b Square Plus c Square Formula Using a2 + b2 Formula?

We know that a2 + b2 = (a + b)2 - 2ab. Replacing b with b + c on both sides:

a2 + (b + c)2 = (a + b + c)2 - 2a (b + c)
a2 + (b2 + c2 + 2bc) = (a + b + c)2 - 2ab - 2ac (∵ (a + b)2 = a2 + b2 + 2ab)
a2 + b2 + c2 = (a + b + c)2 - 2ab - 2ac - 2bc

What is the a^2 + b^2 + c^2 Formula in Algebra?

The a2 + b2 + c2 formula is one of the important algebraic identities. It is read as a square plus b square plus c square. Its a2 + b2 + c2 formula is expressed as a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ca).

How to Simplify Numbers Using the a2 + b2 + c2 Formula?

Let us understand the use of the a2 + b2 + c2 formula with the help of the following example.
Example: Find the value of (22 + 52 + 32) using the a2 + b2 + c2 formula.
To find: (22 + 52 + 32)
Let us assume that a = 2 and b = 5 and c = 3.
We will substitute these in the formula of (a2 + b2 + c2).
a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ca)
= (2 + 5 + 3)2 - 2(2×5 + 5×3 + 3×2)
= 100 - 62 = 38

Answer: (22 + 52 + 32) = 38

How to Use the (a2 + b2 + c2) Formula Give Steps?

The following steps are followed while using (a2 + b2 + c2) formula.

  • Firstly observe the pattern of the numbers whether the three numbers have ^2 as individual power or not.
  • Write down the formula of (a2 + b2 + c2).
  • a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ca).
  • Substitute the values of a, b and c in the a2 + b2 + c2 formula and simplify.
Math worksheets and
visual curriculum