Euclid’s Fifth Postulate

The original version of Euclid’s Fifth Postulate is as follows:

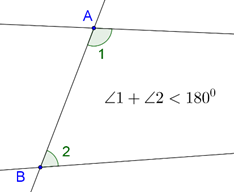
“If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the straight lines, if produced indefinitely, will meet on that side on which the angles are less than two right angles.”

Consider the following figure, in which the two lines meet (when extended) on that side on which the interior angles sum to less than two right angles:

In a sense, Euclid’s Fifth Postulate says that two parallels will never meet (this seems obvious). As an exercise, construct three more such examples, where the interior angles sum to less than two right angles or \(180^\circ\) (as shown above), and see whether the two lines actually meet or not (when extended).

An alternate statement which is (almost) the same as this version of Euclid’s Fifth Postulate goes as follows:

“Given a line L and a point P not on the line, exactly one line can be drawn through P which is parallel to L.”

This might be easier to visualize. As shown below, P does not lie on L, and exactly one line parallel to L can be drawn through P:

If you compare Euclid’s Fifth Postulate with the other four postulates, you will see that it is more complex, while the others are very basic. This led many mathematicians to believe (for many centuries) that Euclid’s Fifth Postulate is not a fundamental truth but a result which can be derived from the other four postulates. Many tried in vain to do so, but all failed.

We now know why this happened: Euclid’s Geometry is not the only geometry possible. Assuming the Fifth Postulate to be true gives rise to Euclid’s Geometry, but if we discard the Fifth Postulate, other systems of geometry can be constructed (in which even parallel lines could meet!). Such geometries are called non-Euclidean geometries. As we said earlier, these are advanced ideas. For now, just remember that Euclid’s Fifth Postulate is not a universal truth, but as long as we are confined to studying Euclidean Geometry, we assume it to be true.