Convexity and Concavity of Graphs

Convexity / Concavity

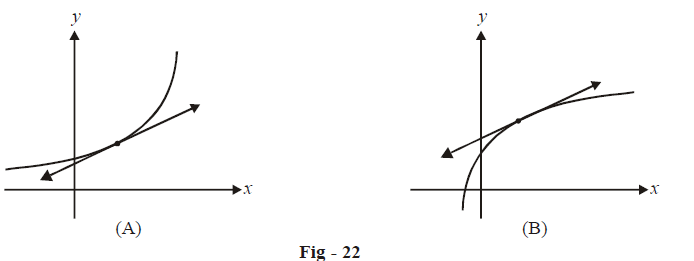
Observe the two graphs sketched in the figure below. What is the difference between them?  Although they are both increasing, the first graph’s rate of increase is itself increasing whereas the rate of increase is decreasing in case of the second graph.

On graph A, if you draw a tangent any where, the entire curve will lie above this tangent. Such a curve is called a concave upwards curve. For graph B, the entire curve will lie below any tangent drawn to itself. Such a curve is called a concave downwards curve.

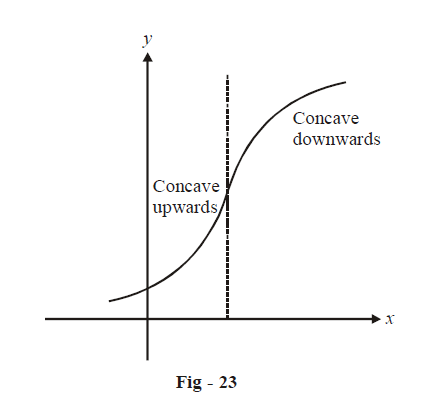
The concavity’s nature can of course be restricted to particular intervals. For example, a graph might be concave upwards in some interval while concave downwards in another.

How would concavity be related to the derivative(s) of the function?

We can determine this intuitively. Let us again consider graph A in Fig.- 22. This is a concave upwards curve. We see that the rate of increase of the graph itself increases with increasing x, i.e. rate of increase of slope is positive:

\[\begin{align}&\frac{d}{{dx}}\left( {\frac{{dy}}{{dx}}} \right) > 0\\ \Rightarrow \qquad &\frac{{{d^2}y}}{{d{x^2}}} > 0\end{align}\]

Similarly, for a concave downwards curve,

\[\begin{align}\frac{{{d^2}y}}{{d{x^2}}} < 0\end{align}\]

The nature of concavity is simply related to the sign of the second derivative. This can of course be proved more rigorously.

We now finally come to what we mean by point of inflexion. Consider \(f(x){\rm{ }} = {x^3}\)  again

\[\begin{align}  & f'\left( 0 \right) = f''\left( 0 \right) = 0\\  \\  & f''\left( x \right) < 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{for}}{\mkern 1mu} {\mkern 1mu} x < 0\\  \\  & {\rm{and}} > 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{for}}{\mkern 1mu} {\mkern 1mu} x > 0\\  \\   \Rightarrow \qquad &  f''\left( x \right){\text{ changes sign as }}x{\text{ crosses 0}}{\rm{.}}\\  \\   \Rightarrow \qquad &  f\left( x \right){\text{changes the nature of its concavity as }}x{\text{ crosses 0}}{\rm{.}}  \end{align}\]

Such a point is called a point of inflexion, a point at which the concavity of the graph changes.

Notice that \(f''\left( a \right) = 0\) alone is not sufficient to guarantee a point of inflexion at \(x=a.\) \(f''( x)\) must also change sign as x crosses \(a.\)

For example, in \(f\left( x \right) = {x^4},\,\,\,\,f''\left( 0 \right) = 0\)  but \(x=0\) is not a point of inflexion since \(f''\left( x \right)\)  does not change its sign

as \(x\) crosses 0. From the higher order derivative test, we know that \(x=0\) is a local minimum for\(f\left( x \right) = {x^4}\).

You should view the entire discussion above in one coherent flow and should not treat the various facts presented independent of each other; you must realise how they are interlinked. The first order derivative test follows from the second order derivative test, which follows from the higher order derivative test. For this purpose, the entire discussion has been summarized in the table below:

We will be using FODT and SODT interchangeably to determine extrema for a given function. The need for the HODT  will hardly arise.