Co-ordinate geometry is a marriage of pure geometry and algebra, and is indispensable in all branches of science today. Many of you must be pretty familiar with the general outline of this subject.
We will restrict ourselves to 2-dimensional (plane) co-ordinate geometry in the following pages. Later on, we will also get the chance of studying 3-dimensional co-ordinate geometry.
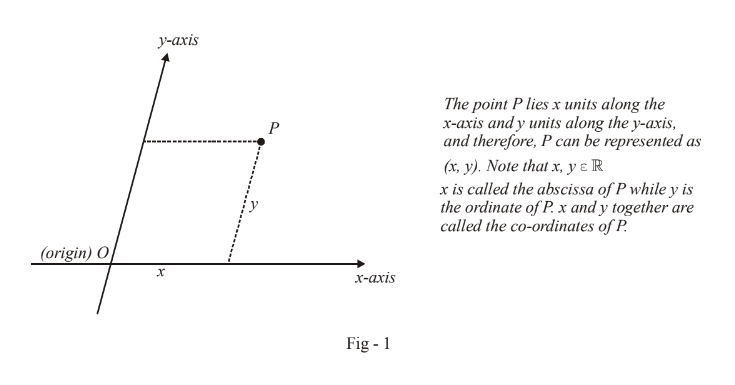
The basic idea in co-ordinate geometry, as has been mentioned earlier, is to study the properties of geometrical figures such as straight lines, circles, parabolas etc through the use of numbers. The core concept is that on a 2-dimensional (Euclidean) plane, any point can be represented by a pair of real numbers, using two non-parallel straight lines. The point where these two non-parallel reference lines meet is termed the origin of the reference axis. By convention, one axis is called the x-axis and one the y-axis. Any point on the plane can now be determined in reference to this reference axes as described in the figure below:
Conversely, given the co-ordinates x and y of a point P, we can easily determine its location by moving x units along the x-axis and then y-units parallel to the y-axis.
Notice that as long as the two axes are non-parallel, the entire plane is representable using these two axes as reference. These two axes in general can be at any non-zero angle to each other.
However, it is almost always the case (out of convenience) that the two axis are taken at right angles to each other. Such axes are called Rectangular Axes. We will always be using Rectangular Axes in our discussion from now onwards.
With this introduction, we start with the most elementary of geometric figures: line segments and lines (and other geometric figures obtainable from these elementary ones, like polygons).
