visual curriculum
Table of Contents
| 1. | Introduction |
| 2. | Why are Angles Important? |
| 3. | Example Questions & Answers |
| 4. | Standard Systems Used to Measure Angles |
| 5. | FAQ’s |
| 6. | Summary |
| 7. | External References |
18th November 2020
Reading Time: 4 minutes
Lines and angles- the first concepts of geometry that a student studies. A line is a set of points, while an angle is made when two rays intersect. A ray is a line, which extends infinitely in one direction.
When two rays originate from a common point, the inclination of one ray on another is called an angle.

Also read:
The geometry creates space for students to draw and learn 2D and 3D shapes. But where does it begin? Measuring an angle can either require simple mathematical equations or more complex geometry.
To measure an angle, you generally need a protractor. Download the PDF below to read why angles are important and different systems to measure an angle.
| 📥 | How to Find the Measure of an Angle? |
Why are Angles Important?
The uses of angles are vast ranging from fun uses like in a game of carrom to more complex ones like planetary motion.
Construction, architecture, sports, engineering, art, dance, etc. make use of the concept of angles. That apart, scientists and astronomers depend on the angles that celestial bodies make to study their movement and get down to concrete conclusions.
In the measurement, you will be dealing with the vertex of the angle, which is where the two lines meet to form an angle. Angles are measured in degrees. Measuring angles can make us better prepared to deal with numbers and measurements as well as in tapping into our visual abilities.

Example Questions & Answers
Let us look at some sample questions and answers on How to find the measure of an angle -
Q.1 What is the sum of the interior angles of a triangle?
Answer- The sum of the interior angles of a triangle is 180 degrees.
| 180° |
Q.2 Two of the interior angles of a triangle measure 50 and 45. What is the greatest measure of any of its exterior angles?
Answer- The interior angles of a triangle must have measures whose sum is 180, so the measure of the third angle must be
180 − (50 + 45) = 85
By the Triangle Exterior-Angle Theorem, an exterior angle of a triangle measures the sum of its remote interior angles; therefore, to get the greatest measure of any exterior angle, we add the two greatest interior angle measures:
50 + 85 = 135
| 135 |
Q.3 Two angles are supplementary and have a ratio of 1:4. What is the size of the smaller angle?
Answer- Since the angles are supplementary, their sum is 180 degrees. Because they are in a ratio of 1:4, the following expression could be written:
x + 4x = 180
5x = 180
x = 36
| 36 |
Q.4 In a given triangle, the angles are in a ratio of 1:3:5. What size is the middle angle?
Answer- The sum of the angles of a triangle is 180
, and given that the angles are in a ratio of 1:3:5, let the measure of the smallest angle be
x, then the following expression could be written:
x + 3x + 5x = 180
9x = 180
x = 20
If the smallest angle is 20 degrees, then given that the middle angle is in the ratio of 1:3, the middle angle would be 3 times as large, or 60 degrees.
| 60° |
Q.5 Two interior angles of a triangle add up to 64 degrees. What is the measure of the other angle?
Answer- The sum of the three angles of a triangle adds up to 180 degrees. Subtract 64 degrees to determine the third angle.
180 − 64 = 116
| 116 |
Do you know the standard systems used to measure angles?
Here are the various standard systems used to measure angles. We have simplified them for you to help your students
1. Degree
A degree is a measurement of a plane angle, representing 1/360 of a full rotation. It is usually denoted with °.
Why is 360° considered as the angle made for one complete rotation?
It is believed that the Babylonians invented the degree and always counted in base-60. This is where the initial ideas of 360 came about. It was considered due to it’s readily divisible nature by many numbers. For example, 360 is divisible by every number between 1 to 10 except 7. Science also confirms that the Earth takes close to 365 days to complete one revolution around the sun. Most major calendars have close to 360 days in a year.
Degrees are measured using protractors and is one of the most common methods of measuring angles.

2. Radian
Radian measure of an angle is defined as the ratio of the length of the arc that the angle subtends of a circle, divided by the length of the radius of the same circle.
This ratio will give you the radian measure of the angle.
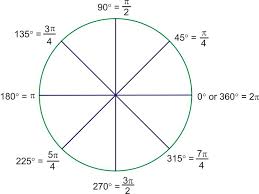
A radian does not have a unit. Why? Because it is the ratio of two lengths, hence the units get canceled.
3. Revolution
A revolution is said to be the simplest, most natural unit of measure for geometric angles. Revolutions help students understand the deeper meaning of angles. This is because an angle is basically a subdivision of a circle rather than the sum of a few degrees. For example, it’s easier for students to understand, “a right angle is quarter of a circle” than, “a right angle is 90°
Introducing your students to revolutions alongside degrees will help them grasp the concepts of angles in a much more stronger manner. Here’s an illustration which you can use to explain the difference between the three systems of measuring angles
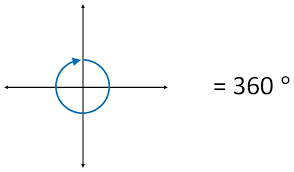
Apart from the standard systems, it is good to build the idea early on in the student that the unit to measure an angle is an angle. It does not “have” to be measured using degrees. They can create their own system of measurement and use that to measure angles.
It is easier for students to develop a sense of measuring an angle using a wedge rather than a protractor. A paper wedge protractor can be made by folding a circle in halves four times until 16 wedges (or sectors) have been formed. If the paper is see through then the paper can be placed over a corner of a polygon or an angle ray. The number of wedges can be counted.
Encourage your students to discover new methods of measuring angles and who knows, in the years to come, their method may become the conventional method.
Summary
To summarize:
- Two rays having the same endpoint create an angle. Angles can be found in various objects around us whether it is a pair of scissors, a hockey stick, or a chair.
- The point at which they intersect is called a vertex which is just the common endpoint of rays/ line segments. When naming an angle, the vertex is always in the centre.
- Measuring angles can help to improve spatial understanding and the relationship between numbers and measurements, not only are useful in academics but learning about angles helps us to understand and use the things around us.
We hope you found this article on how to find the measure of an angle interesting and informational. Feel free to share this article. Make sure you revise these concepts regularly until they have been understood completely as they are basic and foundational. Spend 30 to 45 minutes regularly learning, understanding, and practicing concepts. You can learn more about angles with us, sign up for a free class.
About Cuemath
Cuemath, a student-friendly mathematics and coding platform, conducts regular Online Classes for academics and skill-development, and their Mental Math App, on both iOS and Android, is a one-stop solution for kids to develop multiple skills. Understand the Cuemath fee structure and sign up for a free trial.
Frequently Asked Questions (FAQs)
How to find the measure of an angle in a circle?
A circle has a total of 360 degrees all the way around to the center, if the central angle determining a sector has an angle measure of 60 degrees, then the sector takes up 60/360 or 1/6, of the degrees all the way around. In that case, the sector has 1/6 the area of the whole circle.
How to find the measure of an arc with an inscribed angle?
An inscribed angle has its vertex on the circle, and the sides of the angle lie on two chords of the circle. The measure of the inscribed angle is half that of the arc that the two sides cut out of the circle.
How to find the measure of an interior angle?
An inscribed angle has its vertex on the circle, and the sides of the angle lie on two chords of the circle. The measure of the inscribed angle is half that of the arc that the two sides cut out of the circle.
What is degree measure and how to find the degree measure of an angle?
An angle is measured in degrees, minutes, and seconds in this system. A degree is represented as º.
1 right angle = 90 degrees or 90º.