3/4 As A Decimal
In this interesting mini-lesson, we will learn how to convert 3/8 as a decimal. While doing so, we will also explore other fraction to decimal conversions such as 3/2 as a decimal and 1/10 as a decimal.
You can check out the interactive questions to know more about the lesson and try your hand at solving a few interesting practice questions at the end of the lesson.
Before we get started, let's see what Mr. Mike is confused about.
Mr. Mike asks John, "Can you please tell me which is smaller, 3/4 or 0.34?"
John is clueless as both the numbers do not have the same form.
He can answer the question with ease if he could represent both in the same form i.e. either both in decimal or in fraction.

Let's see how to do that.
Lesson Plan
What Is 3/4 As a Decimal?
The word "Decimal" is derived from the Latin word Decimus which means one-tenth. The decimal system has base 10
1/10 as a decimal means 0.1 and 1/100 represents 0.01
When we convert a fraction into decimal form, we convert it into a number that has a denominator 1. So, the numerator takes a form that has a decimal point in it.
The decimal form of \(\dfrac{3}{4}\,\) is 0.75
Visualizing 0.75
Look at the square grid having 100 grids. Each square here will represent the fraction \(\dfrac{1}{100}\)
0.75 = 0.5 + 0.25
0.5 = 0.50 which means 50 out of 100 and 0.25 denotes 25 out of 100

Let's proceed to learn the methods to convert 3/4 into decimal form.
How to Change 3/4 As a Decimal?
The fraction \(\dfrac{3}{4}\,\)can be converted to a form with denominator 1 by finding its decimal form.
To get the decimal form of \(\dfrac{3}{4}\,\), various approaches are possible.
Method 1
In this method, we use long division.

Here, Numerator = 3 and Denominator = 4. Let's divide 3 by 4

We obtain the remainder 3 on division. So, we continue the division till we get remainder 0

A decimal point is put after 3 and we add a 0 to continue division. This also introduces a decimal point in the quotient after 0. Now, we have the remainder 30
\[4\times 7 = 28\] and, \[30-28=2\]
Remainder = 2. So, we continue dividing.
Put one more 0 after the decimal in the dividend and bring it down to make the remainder 20 now.
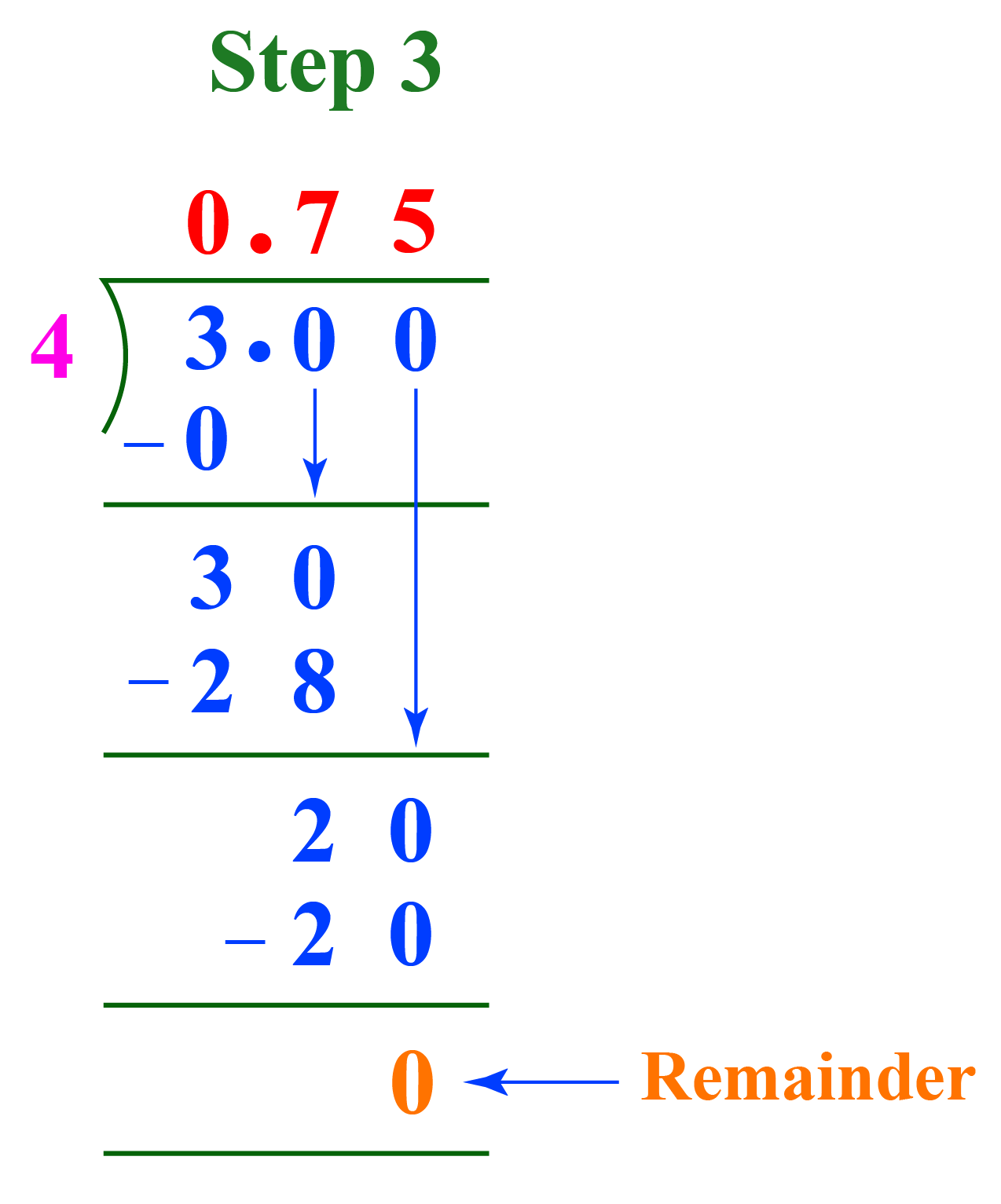
\(4\times 5 = 20\) and \(20-20=0\)
Remainder = 0. So, we stop dividing. The quotient gives the decimal form of \(\dfrac{3}{4}\).
\(\dfrac{3}{4}=0.75\text{Decimal form}\)

We can use this method for converting any fraction to decimal form.
Example: Let's try representing the fraction 3/8 as a decimal.
Numerator = 3, Denominator = 8
Let's use long division.
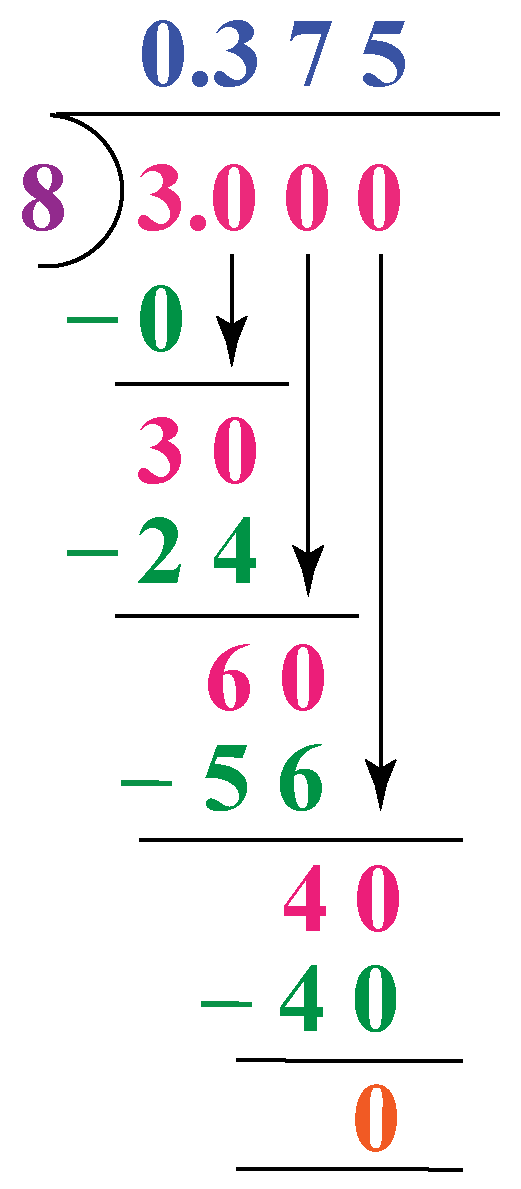
We obtain, \[\dfrac{3}{8} = 0.375\]
Method 2
The other method is to convert the fraction into its equivalent fraction with a denominator as a power of 10
Example: Consider \(\dfrac{3}{2}\), we can express 3/2 as a decimal by converting it into its equivalent fraction with denominator 10
\begin{align} \dfrac{3}{2}&=\dfrac{3\times 5}{2\times 5}\\&=\dfrac{15}{10}\\&=1.5\end{align}
In the fraction \(\dfrac{3}{4}\), denominator = 4
We need to look for a multiple of 4 which is a power of 10
The first power of 10 is 10 which is not a multiple of 4. So, let's look at the second multiple i.e. 100, which is a multiple of 4

\begin{align} \dfrac{3}{4}&=\dfrac{3\times 25}{4\times 25}\\&=\dfrac{75}{100}\end{align}
Now, observe that there are 2 zeros in the denominator.
So, there will be two digits after decimal in the numerator.
\(\dfrac{3}{4}=0.75\)
We can even convert a decimal to a fraction. For this, we consider the number of digits after the decimal.
Example: Take 0.15, there are two digits after the decimal.
\begin{align} 0.15&= \dfrac{15}{100}\\&=\dfrac{3}{20}\end{align}

- Decimals are used to represent fractions which have a value less than 1
- The decimal system has a base of 10
- To convert a fraction into decimal either of the two methods can be used: a) Long Division b) Using Equivalent Fractions.
Solved Examples
| Example 1 |
Henry wants to express \(\dfrac{3}{2}\,\) as decimal. Can you help him by using the long division method to convert a fraction to decimal?
Solution
Numerator = 3, Denominator = 2
Let's use the long division method.

| \(\therefore\dfrac{3}{2}=1.5\) |
| Example 2 |
Let's consider the question that we saw in the introduction and find an answer to the question that Mr. Mike asked John.
Which is greater, 3/4, or 0.34?
Solution
To answer this question, lets write 3/4 in its decimal form and then compare it with 0.34
\(\dfrac{3}{4}=0.75\)
Now,
\(0.75 > 0.34\)
| \(\therefore\dfrac{3}{4}>0.34\) |

- Without actually finding the decimal form of fractions \(\dfrac{3}{4}\) and \(\dfrac{3}{8}\), can you tell which of the two is greater?
- Can every decimal number be converted into a fraction?
Interactive Questions
Here are a few activities for you to practice.
Select/Type your answer and click the "Check Answer" button to see the result.
Let's Summarize
We hope you enjoyed learning about fractions to decimal with the simulations and practice questions. Now, you will be able to easily solve problems on 3/4 as a decimal, fraction to decimal, 1/10 as a decimal, and other similar conversions.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.
Frequently Asked Questions (FAQs)
1. What is 3/4 as a decimal?
The decimal form of \(\dfrac{3}{4}=0.75\)
2. What is 3/4 as a decimal and percent?
The decimal form of\(\,\dfrac{3}{4}=0.75\) and in percent form it's written as \(75\%\)
3. How do you write 3/4 of an hour?
1 hour = 60 minutes.
\(\dfrac{3}{4}\) of an hour \(=\dfrac{3}{4}\times 60=45\) min.
- Live one on one classroom and doubt clearing
- Practice worksheets in and after class for conceptual clarity
- Personalized curriculum to keep up with school