Applications of Trigonometry
Applications of Trigonometry can be found in different fields in our day-to-day lives. One of the well-known fields is astronomy where trigonometry helps in determining the distances of the Earth from the planets and stars. It is used in constructing maps in geography and navigation. Applications of trigonometry are also used in finding an island's position in relation to the longitudes and latitudes. Even today, some of the technologically advanced methods which are used in engineering and physical sciences are based on the concepts of trigonometry. Let us learn more about the applications of trigonometry and see a few examples related to it.
| 1. | What is the Applications of Trigonometry? |
| 2. | Real-Life Applications of Trigonometry |
| 3. | Trigonometric Ratios |
| 4. | FAQs on Applications of Trigonometry |
What is the Applications of Trigonometry?
Applications of trigonometry are applied in areas such as architecture, celestial mechanics, surveying, etc. The most common fields are astronomy and physics where it helps in finding the distance between the stars and planets, the path in motion, and analysing the waves. Some of the applications include:
- Various fields like oceanography, seismology, meteorology, physical sciences, astronomy, acoustics, navigation, electronics, and many more.
- It is also helpful to find the distance of long rivers, measure the height of the mountain, etc.
- Spherical trigonometry has been used for locating solar, lunar, and stellar positions.
What is Trigonometry?
Trigonometry is considered one of the most significant branches of mathematics. The word trigonometry is formed by combining the words 'Trigonon' and 'Metron' which means triangle and measure respectively. Trigonometry is the study of the relation between the sides and angles of a right-angled triangle. It thus helps in finding the measure of unknown dimensions of a right-angled triangle using formulas and identities based on this relationship. There are three basic functions in trigonometry - sine, cosine, and tangent.

Real-Life Applications of Trigonometry
As we have already discovered, the applications of trigonometry are seen in different fields in real life. Let us look at all these fields briefly to understand the application of trigonometry better.
Trigonometry in Astronomy
Astronomy is one of the most popular fields that use trigonometry as one of the essential applications for the basic functioning of the field. Trigonometric tables were created over decades ago for computations in this field. It helps in determining the distance between the stars and planets. The tables help in locating the position of a sphere and this kind of trigonometry is called spherical trigonometry. This type of trigonometry is called linear algebra and is taught to children at a young age.
Trigonometry in Flight Engineers
There has been significant growth in aviation or flight engineers in terms of functionality because of trigonometry. It helps in determining the speed, direction, and distance of an airplane along with keeping in mind the speed and direction of the wind. The wind plays an important role while landing and taking off to calculate at what angle and what speed is the best for that airplane.
Trigonometry in Navigation
Another use of trigonometry is seen in navigating directions with the help of a compass that provides the straight direction to a destination. Here, trigonometry functions come into play that makes it simple to find the location and also find the distance. The satellite navigation system also uses trigonometric functions such as the law of cosine to calculate simple equations to help in locating the satellites in the earth's orbit 24 hours.
Trigonometry in Measuring Heights
Calculating the height of a mountain or a tall building can be easily found by trigonometry. The height can be determined by measuring the horizontal distance from the base and finding the angle of elevation to the top. This formation will represent a right-angle triangle with three sides, perpendicular, base, and hypotenuse. These three aspects are the necessities of calculating any trigonometric equations. Let us look at an example to understand the measurement of height. A boy is standing near a tree. He looks up at the tree and wonders “How tall is the tree?” The height of the tree can be found without actually measuring it. What we have here is a right-angled triangle, i.e., a triangle with one of the angles equal to 90 degrees. Trigonometric formulas can be applied to calculate the height of the tree, if the distance between the tree and boy, and the angle formed when the tree is viewed from the ground is given.
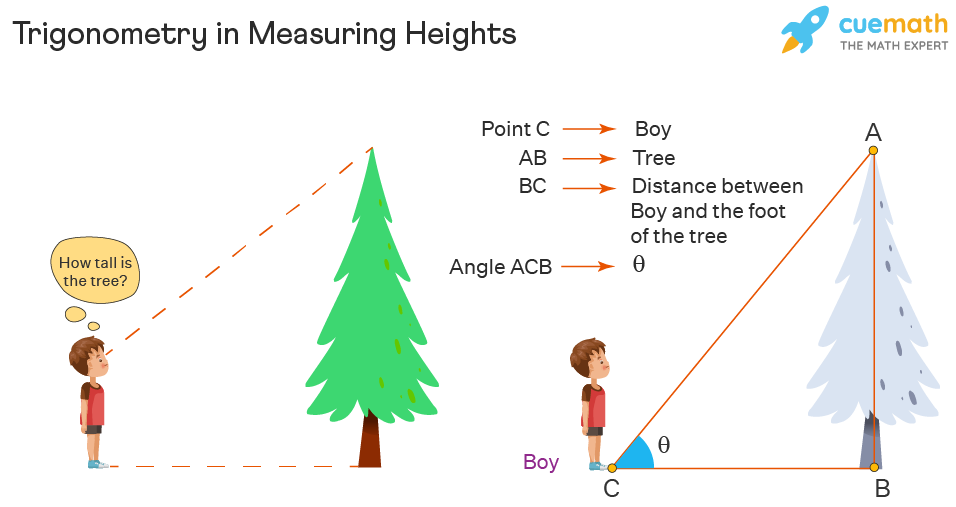
It is determined using the tangent function, such as tan of angle is equal to the ratio of the height of the tree and the distance. Let us say the angle is θ, then
tan θ = Height/Distance between object & tree
Distance = Height/tan θ
Let us assume that distance is 30m and the angle formed is 45 degrees, then
Height = 30/tan 45°
Since, tan 45° = 1
So, Height = 30 m
The height of the tree can be found out by using basic trigonometry formulas.
Trigonometry in Construction
Trigonometry is used in construction sites in measuring ground surfaces and fields. When constructing a building, aspects like roof inclination, rook slopes, perpendicular and parallel walls, light angles, sun shading, etc, require trigonometry. It also helps while installing ceramic tiles and stones while construction.
Other Uses of Trigonometry
Other fields where trigonometry is used are:
- Criminology or crime scenes require the assistance of trigonometry in determining the estimated cause of a collision in a car accident or at what angle was a gun shot.
- Marine biologists use trigonometry to measure the depth of sunlight that affects algae to photosynthesis.
- Trigonometric functions help in describing sound and light waves.
- Trigonometry is used in oceanography to calculate the heights of waves and tides in oceans.
- Calculus is based on trigonometry and algebra.
Trigonometric Ratios
There are basic six ratios in trigonometry that help in establishing a relationship between the ratio of sides of a right triangle with the angle. If θ is the angle in a right-angled triangle, formed between the base and hypotenuse, then
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
The value of the other three functions: cot, sec, and cosec depend on tan, cos, and sin respectively as given below.
- cot θ = 1/tan θ = Base/Perpendicualr
- sec θ = 1/cos θ = Hypotenuse/Base
- cosec θ = 1/sin θ = Hypotenuse/Perpendicular
Related Topics
Listed below are a few topics related to the applications of trigonometry, take a look.
Examples on Applications of Trigonometry
-
Example 1: A man standing at a certain distance from a building, observes the angle of elevation of its top to be 60°. He walks 30 yds away from the building. Now, the angle of elevation of the building’s top is 30°. How high is the building?
Solution:
Let the height of the building be h, and d be the original distance between the man and the building. The following figure depicts the given situation:

We have:
\[\begin{align}
\tan {60^\circ } &= \sqrt 3 \hfill \\
\Rightarrow \frac{h}{d} &= \sqrt 3 \hfill \\
\Rightarrow d &= \frac{h}{{\sqrt 3 }} \hfill \\
\end{align} \]Also,
\[\begin{align}
\tan {30^\circ } &= \frac{1}{{\sqrt 3 }} \hfill \\
\Rightarrow \frac{h}{{d + 30}} &= \frac{1}{{\sqrt 3 }} \hfill \\
\Rightarrow \sqrt 3 h &= d + 30 \hfill \\
\Rightarrow \sqrt 3 h &= \frac{h}{{\sqrt 3 }} + 30 \hfill \\
\Rightarrow h\left( {\sqrt 3 - \frac{1}{{\sqrt 3 }}} \right) &= 30 \hfill \\
\end{align} \]\[ \Rightarrow h = 15\sqrt 3 yd \approx 26\;yd\]
Therefore, the height of the building is about 26 yards.
-
Example 2: A man observed a pole of height 60 ft. According to his measurement, the pole cast a 20 ft long shadow. Find the angle of elevation of the sun from the tip of the shadow using trigonometry.
Solution:
Let x be the angle of elevation of the sun, then
tan x = 60/20 = 3
x = tan-1(3)
or x = 71.56 degreesTherefore, The angle of elevation of the sun is 71.56º.

FAQs on Applications on Trigonometry
What are the Main Applications of Trigonometry?
The applications of trigonometry are seen in different fields in our day-to-day life. Some of the fields are:
- Construction
- Astronomy
- Aviation or field engineering
- Navigation
- Measuring heights of a building
- Criminology
- Marine Biology
What is the Practical Applications of Trigonometric Identities?
Some of the practical applications of trigonometry are used in architecture while calculating the slope of roofs to build a home to drain rainwater or snow. Another practical application is measuring the height of different objects such as a mountain or a tree or a tower.
How to Find Height with Angle of Elevation in Trigonometry?
To find the height with the angle of elevation, we need to use the trigonometric formulas based on which two sides of the right triangle are given.
What are the Basics of Trigonometry?
Trigonometry basics deal with the measurement of angles and problems related to angles. There are six basic trigonometric ratios: sine, cosine, tangent, cosecant, secant and cotangent. All the important concepts covered under trigonometry are based on these trigonometric ratios or functions.
What are the Six Basic Trigonometry Functions?
There are 6 trigonometry functions which are:
- Sine function
- Cosine function
- Tangent function
- Secant function
- Cotangent function
- Cosecant function
visual curriculum