Sin(a - b)
Sin(a - b) is one of the important trigonometric identities used in trigonometry, also called sin(a - b) compound angle formula. Sin (a - b) identity is used in finding the value of the sine trigonometric function for the difference of given angles, say 'a' and 'b'. The expansion of sin (a - b) can be applied to represent the sine of a compound angle(in form of a difference of two angles) in terms of sine and cosine trigonometric functions. Let us understand the sin(a - b) identity and its proof in detail in the upcoming sections.
| 1. | What is Sin(a - b) Identity in Trigonometry? |
| 2. | Sin(a - b) Compound Angle Formula |
| 3. | Proof of Sin(a - b) Formula |
| 4. | How to Apply Sin(a - b)? |
| 5. | FAQs on Sin(a - b) |
What is Sin(a - b) Identity in Trigonometry?
Sin(a - b) is the trigonometry identity for the compound angle that is given in the form of the difference of two angles. It is applied when the angle for which the value of the sine function is to be calculated is given in the form of compound angle for the difference of two angles. Here, the angle (a - b) represents the compound angle.
Sin(a - b) Compound Angle Formula
Sin(a - b) formula is also called the difference formula in trigonometry. The sin(a - b) formula for the compound angle(a - b) can be given as,
sin (a - b) = sin a cos b - cos a sin b,
where a and b are the measures of any two angles.
Proof of Sin(a - b) Formula
The expansion of sin(a - b) formula can be proved geometrically. To give the stepwise derivation of the formula for the sine trigonometric function of the difference of two angles geometrically, let us initially assume that 'a', 'b', and (a - b) are positive acute angles, such that (a > b). In general, sin(a - b) formula is true for any positive or negative value of a and b.
To prove: sin (a - b) = sin a cos b - cos a sin b
Construction: Let OX be a rotating line. Rotate it about O in the anti-clockwise direction to form the rays OY and OZ such that ∠XOZ = a and ∠YOZ = b. Then ∠XOY = a - b.
Take a point P on the ray OY, and:
- draw perpendiculars PQ and PR to OX and OZ respectively.
- Again, draw perpendiculars RS and RT from R upon OX and PQ respectively.
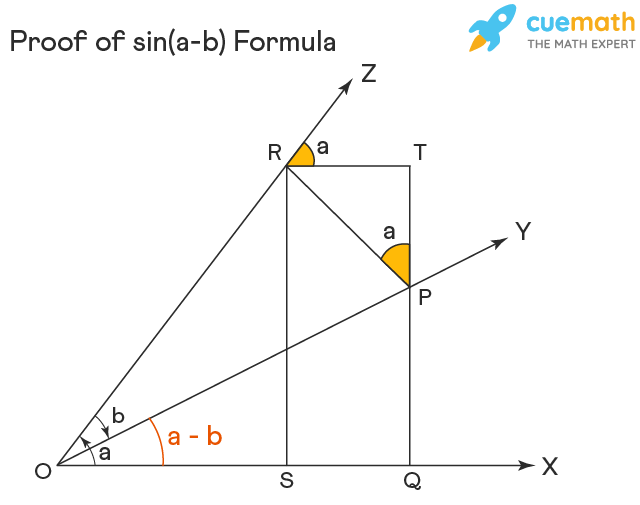
Proof: We will see how we have written ∠TPR = a in the above figure.
- From the right triangle OPQ, ∠OPQ = 180 - (90 + a - b) = 90 - a + b;
- From the right triangle OPR, ∠OPR = 180 - (90 + b) = 90 - b
Now, from the figure, ∠OPQ, ∠OPR, and ∠TPR are the angles at a point on a straight line and hence they add up to 180 degrees.
∠OPQ + ∠OPR + ∠TPR = 180
(90 - a + b) + (90 - b) + ∠TPR = 180
180 - a + ∠TPR = 180
∠TPR = a
Now, from the right-angled triangle PQO we get,
sin (a - b) = PQ/OP
= (QT-TP)/OP
= QT/OP - TP/OP
= RS/OP - TP/OP
= RS/OR ∙ OR/OP - TP/PR ∙ PR/OP
= sin a cos b - cos ∠TPR sin b
= sin a cos b - cos a sin b, (since we know, ∠TPR = a)
Therefore, sin (a - b) = sin a cos b - cos a sin b.
How to Apply Sin(a - b)?
In trigonometry, the sin(a - b) expansion can be used to calculate the sine trigonometric function value for angles that can be represented as the difference of standard angles. We can follow the below-given steps to learn to apply sin(a - b) identity. Let us evaluate sin(60º - 30º) to understand this better.
- Step 1: Compare the sin(a - b) expression with the given expression to identify the angles 'a' and 'b'. Here, a = 60º and b = 30º.
- Step 2: We know, sin (a - b) = sin a cos b - cos a sin b.
⇒ sin(60º - 30º) = sin 60ºcos 30º - sin 30ºcos 60º
Since, sin 30º = 1/2, sin 60º = √3/2, cos 30º = √3/2, cos 60º = 1/2
⇒ sin(60º - 30º) = (√3/2)(√3/2) - (1/2)(1/2) = 3/4 - 1/4 = 2/4 = 1/2
Also, we know that sin(60º - 30º) = sin 30º = 1/2. Therefore the result is verified.
☛Related Topics on sin(a-b):
Here are some topics that you might be interested in while reading about sin (a - b).
Let us have a look a few solved examples for a better understanding of the concept of sin(a - b) formula.
Examples Using Sin (a - b)
-
Example 1: Using the expansion of sin(a - b), find the exact value of sin 135º.
Solution:
Since, the values of sine and cosine functions can be easily calculated for angles 180º and 45º, we can represent 135º as (180º - 45º).
⇒sin(135º) = sin(180º - 45º) = sin180ºcos45º - sin 45ºcos180º = (0)(1/√2) - (1/√2)(-1) = 0 + 1/√2 = 1/√2
-
Example 2: Prove that sin (40° + θ) cos (10° + θ) - cos (40° + θ) sin (10° + θ) = 1/2 using sin(a - b) formula.
Solution:
Here, L.H.S. = sin (40° + θ) cos (10° + θ) - cos (40° + θ) sin (10° + θ)
= sin [(40° + θ) - (10° + θ)]
Applying the formula of sin a cos b - cos a sin b = sin (a - b)]
= sin (40° + θ - 10° - θ)
= sin 30°
= 1/2 = R.H.S.
Hence, proved.

FAQs on Sin (a - b)
What is Sin (a - b)?
There are many compound angle identities in Trigonometry. sin(a - b) is one of the important trigonometric identities also called sine difference formula. Sin(a - b) can be given as, sin (a - b) = sin a cos b - cos a sin b, where 'a'and 'b' are angles.
What is the Formula of Sin (a - b)?
The sin(a - b) formula is used to express the sin compound angle formulae in terms of values of sin and cosine trig functions of individual angles. Sin(a - b) formula in trigonometry is given as, sin (a - b) = sin a cos b - cos a sin b.
What is Expansion of Sin (a - b)
The expansion of sin(a - b) is given as, sin (a - b) = sin a cos b - cos a sin b, where, a and b are the measures of angles.
How to Prove Sin (a - b) Formula?
The proof of sin(a - b) formula can be given using the geometrical construction method. We initially assume that 'a', 'b', and (a - b) are positive acute angles, such that (a > b). Click here to understand the stepwise method to derive sin(a - b) formula.
What are the Applications of Sin(a - b) Formula?
Sin(a - b) can be used to find the value of sine function for angles that can be represented as the difference of simpler or standard angles. Thus, this formula helps in making the deduction of values of trig functions easier. It can also be applied while deducing the formulas of expansion of other double and multiple angle formulas.
How to Find the Value of Sin 15º Using Sin(a - b) Identity.
The value of sin 15º using (a - b) identity can be calculated by first writing it as sin[(45º - 30º] and then applying sin(a - b) identity.
⇒sin[(45º - 30º)] = sin 45ºcos30º - sin30ºcos 45º = (√3/2√2) - (1/2√2) = (√3 - 1)/2√2 = (√6 - √2)/4.
How to Find Sin(a - b + c) Using Sin(a - b)?
We can express sin(a - b + c) as sin((a - b) + c) and expand using sin(a + b) formula as, sin(a - b + c) = sin(a - b)·cos c + sin c·cos(a - b) = cos c·(sin a cos b - cos a sin b) + sin c·(cos a cos b + sin a sin b) = sin a cos b cos c - cos a sin b cos c + cos a cos b sin c + sin a sin b sin c.
visual curriculum