Square Root of 52
The square root of 52 is expressed as √52 in the radical form and as (52)½ or (52)0.5 in the exponent form. The square root of 52 rounded up to 9 decimal places is 7.211102551. It is the positive solution of the equation x2 = 52. We can express the square root of 52 in its lowest radical form as 2 √13.
- Square Root of 52: 7.211102550927978
- Square Root of 52 in exponential form: (52)½ or (52)0.5
- Square Root of 52 in radical form: √52 or 2 √13
| 1. | What Is the Square Root of 52? |
| 2. | Is Square Root of 52 Rational or Irrational? |
| 3. | How to Find the Square Root of 52? |
| 4. | FAQs on Square Root of 52 |
What Is the Square Root of 52?
- The square root of a number is the number whose product with itself gives the initial number.
- Square root of 52 is √52 = 7.2111
- Square root of 52 can be represented as √52 and (52)1/2
- The square root of 52 is a non-repeating and non-terminating number.
Thus, 52 is not a perfect square.
Is Square Root of 52 Rational or Irrational?
A number is called rational if it can be represented in the form of p/q where q ≠ 0.
The square root of 52 is a number that cannot be represented in this form.
Therefore, the square root of 52 is an irrational number.
How to Find the Square Root of 52?
We will now calculate the square root of 52 using two different methods.
Square Root of 52 Using Approximation Method
Step1. Find two perfect squares between which 52 lies. The two perfect squares are 49 (72) and 64 (82) between which 52 lies. So, we can say that the square root of 52 will be greater than 7 but less than 8 (7 < √52 < 8).
Therefore, the whole number part of the square root will be 7.
Step2. Now for estimating the decimal part, we will use the formula:
(Given number - Lower perfect square) / (Bigger perfect square - Lower perfect square)
Therefore, the decimal part will be = (52-49) / (64-49) = 3/15 = 0.2
So, the approximate square root of 52 will be 7.2
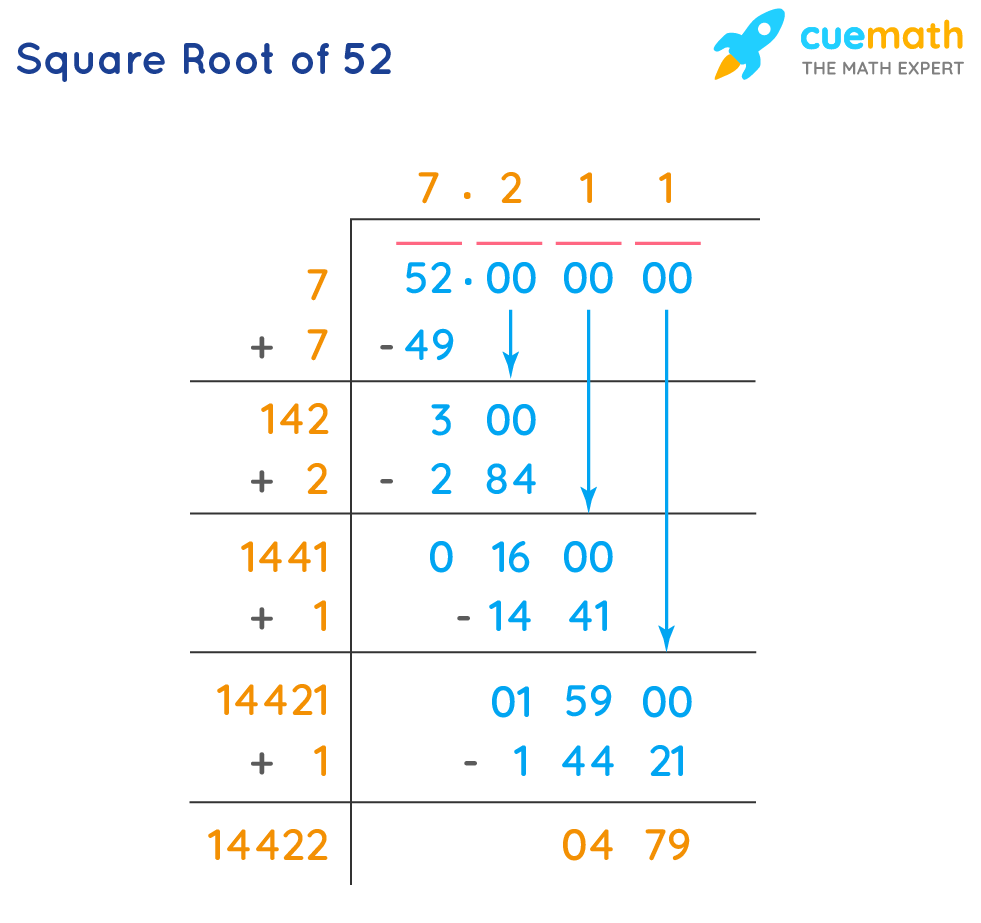
Square Root of 52 by Long Division
With the help of the steps given below, we will now find the square root of 52 by the long division method.
- Start grouping the digits from the right side in pairs of two by putting a bar on top of them. As there are only two digits in 52, we have only one pair.
- Find a number whose product with itself results in a number less than or equal to 52. The number will be 7 as 7 × 7 = 49.
- We get the quotient 7 and the remainder as 3 (52 - 49) and by adding 7 with itself we get the new divisor as 14. As no more numbers are left in the dividend, add a decimal after the dividend and quotient.
- Now add three pairs of zero after the decimal in the dividend part and bring down the first pair of zeros.
- Look for a number(n) such that 14n × n results in a number less than equal to 300. Here n will be 2 as 142 × 2 = 284 (less than 300)
- Bring down the next pair of zeros down and repeat the above step till the last pair of zeros.
So, we get a square root of √52 = 7.211 by the long division method.
Explore square roots using illustrations and interactive examples.
Important Notes:
- The number 52 is not a perfect square.
- The square root of 52 is an irrational number.
- The square root of -52 is an imaginary number.
Square Root of 52 Solved Examples
-
Example 1: Find the square root of 52 by prime factorization method?
Solution:
Prime factorization of 52: 22 × 13
Prime factors of 52 in pairs: (2 × 2) × 13
Square root of 52: √((2 × 2) × 13) = √(22 × 13)
Therefore, √52 = 2√13 -
Example 2: Tyler wants to know the smallest multiple of 52 which is a perfect square. Can you help Tyler to find it out?
Solution:
A perfect square is a number whose factors are the square of a number.
The prime factorization of 52 = 22 × 13
To make it a perfect square we need to multiply it by 13.
Therefore, 13 × 52 = 676 is a perfect square
Hence, 676 is the smallest multiple of 52 which is a perfect square whose square root is ±26. -
Example 3: The half of the square root of 52 is the square root of what number?
Solution:
The square root of 52 in simplified form is √52 = 2√13
Now the half of the square root of 52 will be
√52/2 = ((2√13)/2 = √13
Therefore, the half of the square root of 52 is equal to the square root of 13.

FAQs on the Square Root of 52
What is the Value of the Square Root of 52?
The square root of 52 is 7.2111.
Why is the Square Root of 52 an Irrational Number?
Upon prime factorizing 52 i.e. 22 × 131, 13 is in odd power. Therefore, the square root of 52 is irrational.
What is the Square of the Square Root of 52?
The square of the square root of 52 is the number 52 itself i.e. (√52)2 = (52)2/2 = 52.
If the Square Root of 52 is 7.211. Find the Value of the Square Root of 0.52.
Let us represent √0.52 in p/q form i.e. √(52/100) = 0.52/10 = 0.721. Hence, the value of √0.52 = 0.721
Evaluate 12 plus 19 square root 52
The given expression is 12 + 19 √52. We know that the square root of 52 is 7.211. Therefore, 12 + 19 √52 = 12 + 19 × 7.211 = 12 + 137.011 = 149.011
What is the Value of 9 square root 52?
The square root of 52 is 7.211. Therefore, 9 √52 = 9 × 7.211 = 64.900.
visual curriculum