Translation Math
In the 19th century, Felix Klein proposed a new perspective on geometry known as transformational geometry. Most of the proofs in geometry are based on the transformations of objects. There are four types of transformations possible for a graph of a function (and translation in math is one of them). They are:
- Rotations
- Translations
- Reflections
- Dilation
In this chapter, we will learn about translation in mathematics using translation math definition and translation math examples. Do try your hand at a few translation math problems on translation geometry at the end of the page.
What is Translation in Math?
Translation Math Definition
A translation in math moves a shape left or right and/or up or down. The translated shapes look exactly the same size as the original shape, and hence the shapes are congruent to each other. They just have been shifted in one or more directions. Since it is just moving of the shape from one place to other, there is no change in the shape.
The direction or the path of this change in position of the object can vary i.e., initially the object can move left, then turn right, and so on. While translating, all the points on the shape will shift by the same number of units. For example, if one point shifts 2 units to the right, then all the points will also move 2 units to the right.
Translation is one of the transformations in math. When a shape has been transformed, the original shape is called the preimage and the vertices are usually labeled using uppercase letters (Example: ABCD). The translated shape is called the image and the vertices are labeled using uppercase letters with a “prime” next to each (Example: A′B′C′D′, and is pronounced “A-prime, B-prime, C-prime, D-prime”).
Translation in Geometry Example
In the below figure, the preimage is ABC and its image is A'B'C'. Here, ABC is translated in the following two ways (one after the other) to form A'B'C'.
- Moved up (vertically) by 3 units and then
- Moved right (horizontally) by 2 units
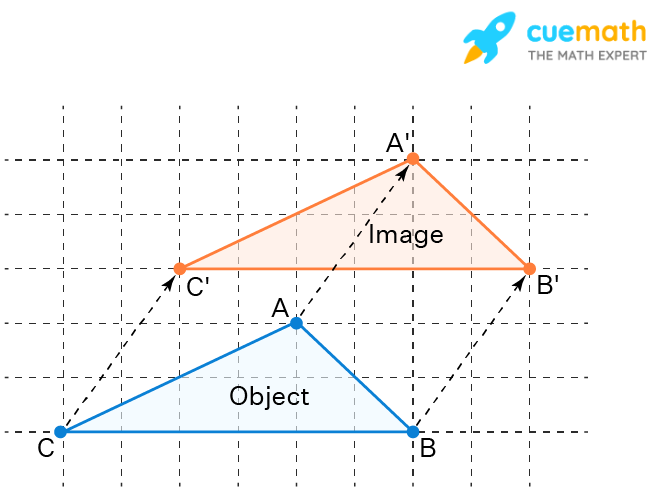
Note that while translating the triangle to the left/right/up/down, we moved all the points of the triangle by an equal number of units in the same direction.
Preimages and Images of Translation
As we have just seen, a shape before translations are applied is known as "preimage" and the shape that is obtained after the application of translations is known as "image. In simple words:
- "Preimage" is the shape before translation.
- "Image" is the shape after translation.
Look at the following figure where ABCD is the preimage and A'B'C'D' is the image of ABC.

Translations on the Coordinate Plane
Any object represented in the coordinate plane can be translated horizontally (left/right) or vertically (up/down). Let us look at the last example to understand translations on the coordinate plane. A graph is represented in the coordinate plane as shown in the figure. While translating, the quadrilateral is shifted 5 units horizontally to the right and 1 unit vertically upward, which means the new translated function for the given figure would be
(x, y) → (x + 5, y + 1)
By this time, you might have got an understanding of the process of writing the translations. Left/right affect the x-coordinate and up/down affect the y-coordinate of a point. Here are the rules of translations.
Translation Rules
- When the shape is moved towards the left by k units, then replace x with x - k.
- When the shape is moved towards the right by k units, then replace x with x + k.
- When the shape is moved up by k units, then replace y with y + k.
- When the shape is moved down by k units, then replace y with y - k.
Example: What are the new coordinates when the translation (x, y) → (x - 2, y + 3) is applied to the point (2, 5).
Solution:
The coordinates of old point (preimage) are (x, y) = (2, 5). Now, applying the given transoformation to this point,
x - 2 = 2 - 2 = 0
y + 3 = 5 + 3 = 8
Thus, the coordinates of the translated point (image) are (0, 8).
How to Graph Translations in Math?
To graph the translation of a shape, we follow the steps below:
- Identify the vertices of the shape.
- Apply the given transformation on each of the vertices to find the new vertices (as shown in the above example).
- Then just plot the new points on the coordinate plane and join them as per the given shape.
Example: A shape is formed with vertices (1, 8), (−3, −5), (−4, 7), and (−6, −2). Plot the image of this shape with respect to the translation (x, y) → (x + 6, y + 1).
Solution:
Let us compute the new coordinates of each of the given vertices.
| Old Coordinates (Before the Translation) |
New Coordinates (After the Translation) |
|---|---|
| A (1, 8) | (1 + 6, 8 + 1) = (7, 9) = A' |
| B (−3, −5) | (-3 + 6, -5 + 1) = (3, -4) = B' |
| C (−4, 7) | (-4 + 6, 7 + 1) = (2, 8) = C' |
| D (−6, −2) | (-6 + 6, -2 + 1) = (0, -1) = D' |
Let us just plot the preimage and the image.

Translations of Functions
The horizontal translations of curves that represent functions work a little differently when compared to the horizontal translations of points on the coordinate plane. Let us observe the example below.

Here, the preimage is f(x) and the image is f(x + 2). Surprisingly, f(x) has moved left by 2 units (instead of right by 2 units) to give f(x + 2). Yes, this is the case with horizontal translations of functions. But this is not the case with vertical translations. Vertical translations work just like how they work with the translations of points on the coordinate plane.
Rules of Translation of Functions
By the above observation, the rules for writing the translated functions can be summarized as follows:
| Translation of Function | When k > 0 | When k < 0 |
|---|---|---|
|
Horizontal Translation |
Moves f(x) "k" units left. | Moves f(x) "k" units right. |
| Vertical Translation f(x) becomes f(x) + k |
Moves f(x) "k" units up | Moves f(x) "k" units down |
Here are some examples:
- f(x - 2) + 3 moves f(x) by 2 units right and 3 units up.
- g(x + 3) - 5 moves g(x) by 3 units left and 5 units down.
Translating Graphs of Functions
To graph the translated graphs, we can move the given graph left/right/up/down using the above rules. Instead of this, we can translate a graph using the coordinates of some points on it. To graph a function translation f(x + k) + C when the graph of the function f(x) is given, just take some important points of the graph (where the shape is changing or taking turns) and find the new x and y coordinates of each point as follows.
- To find the new x-coordinate, set "x + k = old x-coordinate" and solve this for x.
- To find the new y-coordinate, use "old y-coordinate + C".
After finding all the new points, just plot them and join them. This would give the translated graph. You can find an example of this process in the "Examples" section below.
Translation Represented by a Column Vector or Matrix
The translation of any object can be represented by a column vector or column matrix as: \(\left(\begin{array}{l}
a \\ \\
b
\end{array}\right)\),
where a is the number of units to move right or left along the x-axis and b is the number of units to move up or down along the y-axis.
- The number at the top represents the right or left movement. A positive number means moving to the right and a negative number means moving to the left.
- The number at the bottom represents up and down movement. A positive number means moving up and a negative number means moving down.
In the following figure, triangle ABC is being translated to triangle A’B’C':

The translation from ABC to A'B'C' is "2 units right and 3 units down" and the column vector that represents this translation is \(\left(\begin{array}{c}
2 \\ \\
-3
\end{array}\right)\).
Important Notes on Translations Math:
- While translating, all the points will shift by the same number of units.
- The shape or size of the object remains unaffected after translation.
- In the horizontal translation, the domain may be affected, whereas in the vertical translation, the range may be affected.
☛ Related Topics:
Translations Math Examples
-
Example 1: Given the translation (x + 7, y - 3), find the image of the preimage point (3, 8).
Solution:
The given translation is, (x, y) → (x + 7, y - 3).
It is given that (x, y) = (3, 8). So the translated point is,
(x + 7, y - 3) = (3 + 7, 8 - 3) = (10, 5).
Answer: (10, 5).
-
Example 2: If (3, 8) is a point on the graph of a function f(x) then what is the corresponding point of the translated function f(x + 7) - 3?
Solution:
After the given translation:
- New x-coordinate is: x + 7 = 3 ⇒ x = -4
- New y-coordinate is: y = 8 - 3 = 5
Thus, the translated point is (-4, 5).
Answer: (-4, 5).
-
Example 3: The following graph represents a function f(x). Using this, graph the translated graph of f(x - 1) - 3.

Solution:
We can see that the points (-2, 3), (0, 2), (4, 2), and (6, 0) are the points that are defining the shape of the given function. We will compute the new x and y coordinates of each of these points.
Old Points
(of f(x))New Points
(of f(x - 1) - 3)(-2, 3) New x-coordinate: x - 1 = -2 ⇒ x = -1
New y-coordinate: y = 3 - 3 = 0
New point: (x, y) = (-1, 0)(0, 2) New x-coordinate: x - 1 = 0 ⇒ x = 1
New y-coordinate: y = 2 - 3 = -1
New point: (x, y) = (1, -1)(4, 2) New x-coordinate: x - 1 = 4 ⇒ x = 5
New y-coordinate: y = 2 - 3 = -1
New point: (x, y) = (5, -1)(6, 0) New x-coordinate: x - 1 = 6 ⇒ x = 7
New y-coordinate: y = 0 - 3 = -3
New point: (x, y) = (7, -3)Now, we will plot both the given graph (using the old points) and the translated graph (using the new points) on the same plane.

Note that, f(x - 1) - 3 is formed by moving f(x) by 1 unit to the right and 3 units to the down. Hence, our graph is correct.
Answer: The translated graph is drawn by computing the new points.

FAQs on Translations Math
What are Translations Math?
A translation in math (also called an isometry) is a transformation of a shape in a plane that preserves length, which means that the object is transformed without getting its dimensions affected. i.e., it may just be shifted to left/right/up/down.
What is the Process of Graphing Translations?
To graph translations, take care of the following things:
- In the coordinate plane (x, y) → (x + k, y + C) means:
moving horizontally right if k > 0 and left if k < 0.
moving vertically up if C > 0 and down if C < 0. - In case of functions, f(x) → f(x + k) + C means:
moving horizontally left if k > 0 and right if k < 0.
moving vertically up if C > 0 and down if C < 0.
Just take care of the above things and move the shape accordingly while graphing translation.
How Do You Solve Translations?
Translation for any object can be solved in two sections, depending on whether the object is translated horizontally, vertically, or both. A function, f(x), after translation can be represented in the general form as f(x) = f(x + k) + C, where
- k is the number of units translated horizontally (right if k < 0 and left if k >0)
- C is the number of units translated vertically (up if C > 0 and down if C < 0)
What are Translations Rules in Math?
The basic rules to be followed while translating an object are as follows:
- Positive translation in the x-axis or horizontally would mean shifting to the left, while negative horizontal translation means shifting to the right.
- Positive translation in the y-axis or vertically would mean shifting the object upward while negative vertical translation means shifting downward.
- The shape or size of the object remains unaffected after translation.
- All the points in the object will shift by the same number of units and direction.
How to Graph Functions Translations?
To graph the translation f(x + k) + C of a function f(x) in math, follow the steps below.
- Note down some coordinates of the old graph (of f(x)). The process of finding x and y coordinates of a point differs and is explained below.
- Set each old x-coordinate to x + k and solve for x and that gives the new x-coordinate of that point.
- Just add C to the old y-coordinate to find the new y-coordinate.
- Just plot all new points and join them as per the shape of the given curve.
How Do You Translate a Shape in Math?
Translation of an object in the coordinate plane involves alteration in the position of the shape by a given number of units in the given direction. The size and shape remain unaffected after the translation. While translating, all the points will shift by the same number of units. If one point on the shape shifts by 4 units to the left, then all the points also will move 4 units to the left.
visual curriculum