Transformations
Transformations are changes done in the shapes on a coordinate plane by rotation, reflection or translation. In the 19th century, Felix Klein proposed a new perspective on geometry known as transformational geometry. Most of the proofs in geometry are based on the transformations of objects. We can alter any image in a coordinate plane using transformations. The graphics used in video games are better understood with the rules of transformations applied. Let us learn to identify the transformations, understand the rules of transformations of functions, and explore the types of transformations.
| 1. | What are Transformations? |
| 2. | Types of Transformations |
| 3. | Rules For Transformations |
| 4. | Formula of Transformations |
| 5. | FAQs on Transformations |
What are Transformations in Math?
A function, f, that maps to itself is called the transformation, i.e., f: X → X. The pre-image X becomes the image X after the transformation. This transformation can be any or the combination of operations like translation, rotation, reflection, and dilation. The translation is moving a function in a specific direction, rotation is spinning the function about a point, reflection is the mirror image of the function, and dilation is the scaling of a function. Transformations in Math describe how two-dimensional figures move around a coordinate plane.

Types of Transformations
There are four common types of transformations - translation, rotation, reflection, and dilation. From the definition of the transformation, we have a rotation about any point, reflection over any line, and translation along any vector. These are rigid transformations wherein the image is congruent to its pre-image. They are also known as isometric transformations. Dilation is performed at about any point and it is non-isometric. Here the image is similar to its pre-image.
| Transformation | Function | Result |
|---|---|---|
| Rotation | Rotates or turns the pre-image around an axis | No change in size or shape |
| Reflection | Flips the pre-image and produces the mirror-image | No change in size or shape or orientation |
| Translation | Slides or moves the pre-image | No change in size or shape; Changes only the direction of the shape |
| Dilation | Stretches or shrinks the pre-image | Expands or contracts the shape |
Rules for Transformations
Consider a function f(x). On a coordinate grid, we use the x-axis and y-axis to measure the movement. Here are the rules for transformations of function that could be applied to the graphs of functions. Transformations can be represented algebraically and graphically. Transformations are commonly found in algebraic functions. We can use the formula of transformations in graphical functions to obtain the graph just by transforming the basic or the parent function, and thereby move the graph around, rather than tabulating the coordinate values. Transformations help us visualize and learn the equations in algebra.
Transformation of Translation
Translation of a 2-d shape causes sliding of that shape. To describe the position of the blue figure relative to the red figure, let’s observe the relative positions of their vertices. We need to find the positions of A′, B′, and C′ comparing its position with respect to the points A, B, and C. We find that A′, B′, and C′ are:
- 8 units to the left of A, B, and C respectively.
- 3 units below A, B, and C respectively.
This translation can algebraically be translated as 8 units left and 3 units down. i.e. (x,y) → (x-8, y-3)

Transformation of Quadratic Functions
We can apply the transformation rules to graphs of quadratic functions. This pre-image in the first function shows the function f(x) = x2. The transformation f(x) = (x+2)2 shifts the parabola 2 steps right.

Transformation of Reflection
The type of transformation that occurs when each point in the shape is reflected over a line is called the reflection. When the points are reflected over a line, the image is at the same distance from the line as the pre-image but on the other side of the line. Every point (p,q) is reflected onto an image point (q,p). If point A is 3 units away from the line of reflection to the right of the line, then point A' will be 3 units away from the line of reflection to the left of the line. Thus the line of reflection acts as a perpendicular bisector between the corresponding points of the image and the pre-image.
Here is the graph of a quadratic function that shows the transformation of reflection. The function f(x) = x3. The transformation of f(x) is g(x) = - x3 that is the reflection of the f(x) about the x-axis.

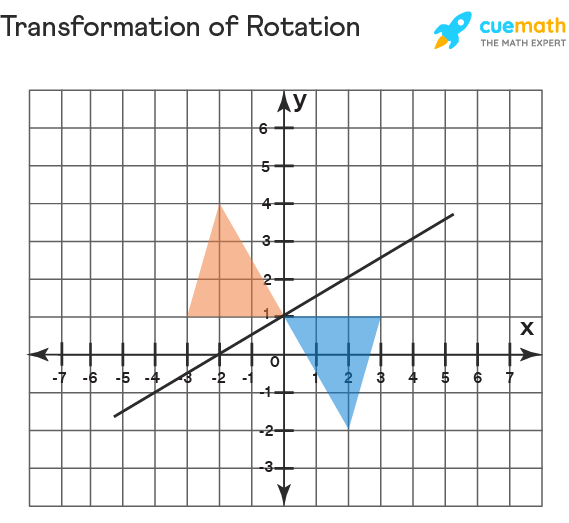
Transformation of Rotation
The transformation that rotates each point in the shape at a certain number of degrees around that point is called rotation. The shape rotates counter-clockwise when the number of degrees is positive and rotates clockwise when the number of degrees is negative. The general rule of transformation of rotation about the origin is as follows.
To rotate 90º: (x,y) → (-y, x)
To rotate 180º (x,y) → (-x,-y)
To rotate 270º (x,y) → (y, -x)
In the function graph below, we observe the transformation of rotation wherein the pre-image is rotated to 180º at the center of rotation at (0,1). Let us observe the rule of rotation being applied here from (x,y) to each vertex. The transformation that is taken place here is from (x,y) → (-x, 2-y)
(-2,4) →(2,-2), (-3,1) → (3,1) and (0,1 ) → (0,1)
Transformation of Dilation
The transformation that causes the 2-d shape to stretch or shrink vertically or horizontally by a constant factor is called the dilation. The vertical stretch is given by the equation y = a.f(x). If a > 1, the function stretches with respect to the y-axis. If a < 1 the function shrinks with respect to the y-axis. The horizontal stretch is given by y = f.(ax). If a > 1, the function shrinks with respect to the x-axis. If a < 1, the function stretches with respect to the x-axis.
Consider a parent function y = x2 +x. After a horizontal shrink by a factor of 5, the altered function becomes 5x2+5x at point (1/5x, y). After a horizontal stretch by factor 1/5, the transformed function becomes 1/5 x2 +1/5 x at a point (5x,y). After a vertical shrink by a factor of 5, the altered function becomes 5x2+5x at point (x, 5y). After a vertical stretch by factor 1/5, the transformed function becomes 1/5 x2 +1/5 x at a point (x, 1/5y).
Formula of Transformations
Let us consider the graph f(x) = x2
- Suppose we need to graph f(x) = x2-3, we shift the vertex 3 units down.
- Suppose we need to graph f(x) = 3x2+ 2, we shift the vertex two units up and stretch vertically by a factor of three.
- Suppose we need to graph f(x) = 2(x-1)2, we shift the vertex one unit to the right and stretch vertically by a factor of 2
- Thus, we get the general formula of transformations as
where k is the vertical shift,
h is the horizontal shift,
a is the vertical stretch and
b is the horizontal stretch.
Likewise, f(x) can be transformed in many ways. This table shows the resultant graph after the transformation is applied on f(x).
| Transformation of f(x) | Transformation of graph | Change (x,y) to |
|---|---|---|
| -f(x) | reflect f(x) over the x-axis | (x,-y) |
| f(-x) | reflect f(x) over the y-axis | (-x,y) |
| f(x)+a | shift f(x) up by a units | (x,y+a) |
| f(x) - a | shift f(x) down by a units | (x,y-a) |
| f(x+a) | shift f(x) left by a units | (x-a,y) |
| f(x-a) | shift f(x) right by a units | (x+a,y) |
| a. f(x) | stretch/shrink f(x) vertically | (x,ay) |
| f(ax) | stretch/shrink f(x) horizontally | (x/a,y) |
Important Notes on Transformations
- Transformations in geometry can be combined. A shape can be reflected or rotated or translated or dilated or can have a combination of these transformations.
- Transformations are expressed algebraically in the graph functions.
☛ Related Topics:
Examples of Transformations
-
Example 1:
How can Mike describe this translation algebraically?

Solution:
Let the orange triangle be the pre-image and the blue triangle be the transformed image.
Represent it on the coordinate plane as (x,y)
Comparing the relative positions of the triangles, we can observe that the blue triangle is placed one position down and 5 positions right.
Answer: Thus, the transition is expressed algebraically as (x,y)→ (x+5, y-1)
-
Example 2:
A point A(1, 3) is translated 4 units to the right. What are the coordinates of the transformed image?
Solution:
Let A be the pre-image.
A' be the image.
If the pre-image is to be moved right, then the x-coordinate undergoes a change of 4 units.
A→ A' = (1,3)→ ((1+4),3)
A → A' = (1,3) → (5,3)
Answer: The coordinates of the transformed image = (5,3)
-
Example 3:
What do the following transformations do to the graph?
i) f(x) → f(x) - 2
ii) f(x) → f(x-2)
Solution:
f(x) → f(x) - 2
The y-coordinate undergoes the change.
Thus, the transformation here is translation 2 units down.
f(x) → f(x-2)
The x-coordinate undergoes the change.
Thus, the transformation here is translation 2 units right.
Answer: i) Translation is 2 units down ii)Translation is 2 units right

FAQs on Transformations
What Are Transformations?
The transformations are the alterations done to a function by translation, reflection, rotation, and dilation. The original image known as the pre-image is altered to get the image.
What are the 4 Types of Transformations?
Translation, reflection, rotation, and dilation are the 4 types of transformations. The translation is moving the shape in a particular direction, reflection is producing the mirror image of the shape, rotation flips the shape about a point in degrees, and dilation is stretching or shrinking the shape by a constant factor.
Why are Transformations Important in Math?
Math is about identifying patterns and understanding the relationships between concepts to work out a solution to a problem. Transformations are important in Math to mainly know the congruence and similarity of figures in a plane. We could alter the position of a point, or a line, or a 2-d shape using the 4 transformations.
How do you Plot a Reflection and What are the Transformations That Take Place?
When we reflect a point across the x-axis, the y-coordinate is transformed and the x-coordinate remains the same. x-coordinate will have the same sign, but the sign of the y-coordinate changes.
What is the Formula For Transformations?
The general formula of transformations is f(x) =a(bx-h)n+k
where k is the vertical shift,
h is the horizontal shift,
a is the vertical stretch and
b is the horizontal stretch.
How do Transformations Work?
The transformations allow us to change the graph of the function to slide, stretch or shrink, rotate.
How do you do Transformations on a Graph?
The following steps are to be followed while we do transformations on a graph.
- Find the parent function f(x) and identify the sequence of the transformations to be made.
- Determine if it is to be reflected over the x-axis or y-axis, to be shifted vertically or horizontally, to be rotated about degrees at a point, or to be stretched or shrunk about the axes using the scaling factor.
- Key-in the coordinates to the parent function following the rules of transformations.
- Plot the transformed function accordingly.
What is the Rule for the Transformations?
Suppose a parent function is f(x), f(x)+a shifts f(x) up by a units, f(x+a) shifts f(x) left by a units, -f(x) reflects f(x) over the x-axis, f(-x) reflects f(x) over the y-axis, a. f(x) stretches or shrinks f(x) vertically and f(a.x) stretches or shrinks f(x) horizontally. These are a few rules for the transformations of graphs.
visual curriculum