Cyclic Quadrilateral
A cyclic quadrilateral is a four-sided polygon inscribed in a circle. It has the maximum area possible with the given side lengths. In other words, a quadrilateral inscribed in a circle depicts the maximum area possible with those side lengths. Let us learn more about a cyclic quadrilateral and its properties in this article.
| 1. | Cyclic Quadrilateral Definition |
| 2. | Properties of Cyclic Quadrilateral |
| 3. | Area of a Cyclic Quadrilateral |
| 4. | Theorems on Cyclic Quadrilateral |
| 5. | FAQs on Cyclic Quadrilateral |
Cyclic Quadrilateral Definition
A cyclic quadrilateral means a quadrilateral that is inscribed in a circle. That means there is a circle that passes through all four vertices of the quadrilateral. The vertices are said to be concyclic. The center of the circle is known as the circumcenter and the radius of the circle is known as the circumradius.
The word "cyclic" is from the Greek word "kuklos", which means "circle" or "wheel". The word "quadrilateral" is derived from the ancient Latin word "Quadri", which means "four-side" or "latus".
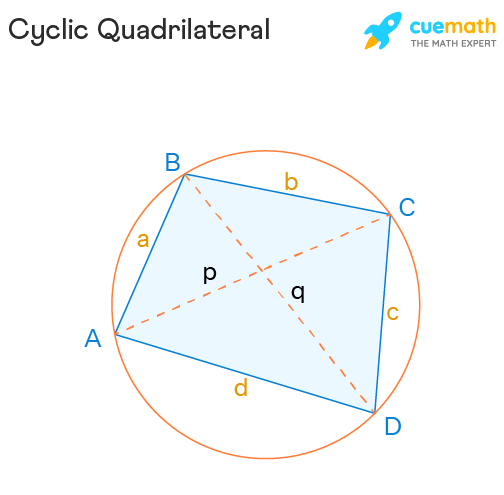
In the figure given below, ABCD is a cyclic quadrilateral with a, b, c, and d as the side-lengths and p and q as the diagonals.
Properties of Cyclic Quadrilateral
The properties of a cyclic quadrilateral help us to identify this figure easily and to solve questions based on it. Some of the properties of a cyclic quadrilateral are given below:
- In a cyclic quadrilateral, all the four vertices of the quadrilateral lie on the circumference of the circle.
- The four sides of the inscribed quadrilateral are the four chords of the circle.
- The measure of an exterior angle at a vertex is equal to the opposite interior angle.
- In a cyclic quadrilateral, p × q = sum of product of opposite sides, where p and q are the diagonals.
- The perpendicular bisectors are always concurrent.
- The perpendicular bisectors of the four sides of the cyclic quadrilateral meet at the center O.
- The sum of a pair of opposite angles is 180° (supplementary). Let ∠A, ∠B, ∠C, and ∠D be the four angles of an inscribed quadrilateral. Then, ∠A+∠C=180° and ∠B+∠D=180°.
Look at an example of cyclic quadrilateral angles given below.

Area of a Cyclic Quadrilateral
The area of a cyclic quadrilateral is \({\sqrt {(s-a)(s-b)(s-c)(s-d)}}\) where a, b, c, and d are the four sides of the quadrilateral and s is the semi perimeter which can be calculated as \(s=(\frac{1}{2})\times (a+b+c+d)\). Heron's formula for a triangle is also derived from this equation.
You will learn more about a cyclic quadrilateral area in the Brahmagupts's theorem on cyclic quadrilaterals explained in the next section.
Theorems on Cyclic Quadrilateral
Apart from the property of a cyclic quadrilateral which says that the sum of opposite angles is always 180°, there are two other theorems on cyclic quadrilateral. Those are explained below:
Ptolemy Theorem of Cyclic Quadrilateral
According to Ptolemy therorem, in a cyclic quadrilateral with successive vertices A, B, C, D, sides a = AB, b = BC, c = CD, d = DA, and diagonals p = AC , q = BD. We can express diagonals in terms of the sides as p × q = (a × c) + (b × d).
Brahmagupta Theorem of Cyclic Quadrilateral
In geometry, Brahmagupta's formula is used to find the area of any quadrilateral with the given sides. It states that the area K of a cyclic quadrilateral whose sides have lengths a, b, c, d is \(K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}\), where s is the semi-perimeter calculated as \(s=(\frac{1}{2})\times (a+b+c+d)\).
► Challenging Questions:
- How do you prove that a quadrilateral is cyclic?
- What is a non-cyclic quadrilateral?
► Important Notes on Cyclic Quadrilateral:
- In a cyclic quadrilateral, the sum of a pair of opposite angles is 180° (supplementary).
- In a cyclic quadrilateral with vertices A,B,C,D, sides a = AB, b = BC, c = CD, and d = DA, and diagonals p = AC and q = BD. We can express diagonals in terms of the sides as: p × q = (a × c) + (b × d).
Related Articles on Cyclic Quadrilateral
Check these interesting articles related to the concept of cyclic quadrilaterals.
Cyclic Quadrilateral Examples
-
Example 1: In the given problem, PQSR is a cyclic quadrilateral, and △PQR is an equilateral triangle, then find the measure of ∠QSR.
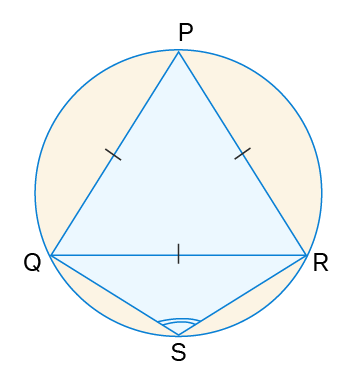
Solution: Given, △PQR is an equilateral triangle. ∴ ∠QPR=60°. Now, we know that opposite angles are supplementary.
∴ ∠QSR + ∠QPR = 180°
From the above two equations we have,
∠QSR + 60° = 180°
∠QSR = 180° − 60°
∠QSR = 120°
∴ The measure of ∠QSR = 120°.
-
Example 2: If the measures of all four angles of a cyclic quadrilateral are given as (4y + 2), (y + 20), (5y - 2), and 7y respectively, find the value of y.
Solution: The sum of all four angles of a cyclic quadrilateral is 360°. So, to find the value of y, we need to equate the sum of the given four angles to 360°.
⇒ (4y + 2) + (y + 20) + (5y - 2) + 7y = 360°
17y + 20 = 360°
17y = 340°
y = 20
∴ The value of y is 20.

FAQs on Cyclic Quadrilateral
What is a Cyclic Quadrilateral?
A cyclic quadrilateral is a four-sided polygon inscribed in a circle. All four vertices of the quadrilateral lie on the circumference of the circle.
Are Opposite Angles of Cyclic Quadrilateral Equal?
No, opposite angles of a cyclic quadrilateral may not be equal. It is true only when a cyclic quadrilateral is a parallelogram. In a parallelogram, opposite angles are congruent.
What are the Properties of the Cyclic Quadrilateral?
Here is a list of the properties of a cyclic quadrilateral:
- All vertices of a cyclic quadrilateral always lie on the circumference of the circle.
- The exterior angle formed if any one side is extended is equal to the sum of the interior angle opposite to it.
- In a cyclic quadrilateral, d1/d2 = sum of product of opposite sides, which shares the diagonals endpoints. In this, d1 and d2 are the diagonals.
- The perpendicular bisectors are always concurrent.
- The perpendicular bisectors of the four sides of the cyclic quadrilateral meet at the center O.
- The area of a cyclic quadrilateral is K=√(s−a)(s−b)(s−c)(s−d) where a, b, c, and d are the four sides of the quadrilateral, and s, the semi perimeter, is defined as s = (1/2)×(a+b+c+d).
Can a Parallelogram be a Cyclic Quadrilateral?
Yes, for a parallelogram to be a cyclic quadrilateral, the opposite angles of that parallelogram should be supplementary. And all four vertices must lie on the circumference. Hence, a parallelogram can be a cyclic quadrilateral.
What is the Sum of Opposite Angles of a Cyclic Quadrilateral?
The sum of opposite angles of a cyclic quadrilateral is always 180°.
How to Find Area of Cyclic Quadrilateral?
The area of a cyclic quadrilateral can be found by using the formula A = √(s−a)(s−b)(s−c)(s−d), where,
A = area
a, b, c, and d = lengths of four sides of the quadrilateral
s = semi-perimeter = (1/2)×(a+b+c+d).
visual curriculum