Semi perimeter of Triangle
The semi perimeter of a triangle is half the sum of all its sides. A triangle is a polygon with three sides, three vertices, and three interior angles that add up to 180°. While the perimeter of a triangle is calculated by adding all its sides, the semi perimeter of a triangle is half the value of the perimeter. Let us study more about the semi perimeter of triangle in this article.
| 1. | What is the Semi perimeter of Triangle? |
| 2. | Semi perimeter of Triangle Formula |
| 3. | How to Find the Semi perimeter of Triangle? |
| 4. | FAQs on Semi Perimeter of Triangle |
What is the Semi Perimeter of Triangle?
The semi perimeter of a triangle is calculated by dividing the perimeter of the triangle by two. 'Semi' means half, that is why the semi perimeter of a triangle is half the value of the perimeter. The semi perimeter of a triangle is used to calculate the area of a triangle using Heron's formula. The semi perimeter of a triangle is expressed in linear units like inches, yards, centimeters, and so on. Now, let us read about the formula that is used to find the semi perimeter of triangle.
Semi Perimeter of Triangle Formula
We know that the perimeter of a triangle is the sum of the lengths of all its sides. If we consider a triangle with side lengths 'a', 'b', and 'c', the perimeter can be calculated with the help of the formula, Perimeter = a + b + c. Using this formula, the formula for the semi perimeter of triangle is derived as: Semi perimeter of triangle = (a + b + c)/2
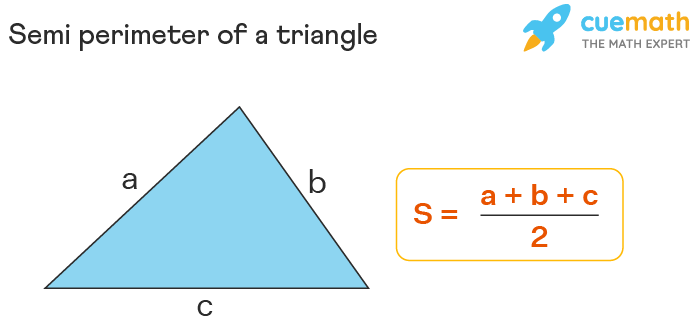
How to Find the Semi Perimeter of Triangle?
If the length of all the sides of a triangle is given, we can calculate the semi perimeter by adding the sides and dividing the sum by 2.
Example: Find the semi perimeter of a triangle with sides 3 units, 4 units, and 5 units.
Solution:
The sides of the triangle are given as: 3 units, 4 units, and 5 units
We will use the formula for the semi perimeter of triangle, Semi perimeter = (a + b + c)/2
Substituting the values in the formula: Semi perimeter = (a + b + c)/2 = Semi perimeter = (3 + 4 + 5)/2 = 12/2 = 6 units.
Therefore, the semi perimeter of the triangle is 6 units.
Use of the Semi perimeter of Triangle
The semi perimeter of a triangle is used to determine the area of triangles using Heron's formula when the length of all three sides is given. This formula solely depends on the lengths of all the sides of a triangle. It contains the term "s" which represents the semi perimeter, which is obtained by dividing the perimeter of a triangle by two. The Heron's formula is expressed as, √[s(s-a)(s-b)(s-c)], where 's' = Semi Perimeter of triangle; and 'a', 'b', 'c' are the three sides of the triangle. So, after calculating the semi perimeter of triangle, the value of 's' is placed in the Heron's formula along with the other sides. This gives the area of a triangle whose three sides are given.
Example: Find the area of a triangle with side lengths 6 units, 7 units, and 9 units.
Solution: The sides of the triangle are given as 'a' = 6 units, 'b' = 7 units, and 'c' = 9 units
The area of the triangle can be calculated using Heron's formula, √[s(s-a)(s-b)(s-c)], where 's' = Semi Perimeter of triangle; and 'a', 'b', 'c' are the three sides of the triangle. Let us first calculate the semi perimeter of the triangle with the help of the formula:
Semi perimeter = (a + b + c)/2
Substituting the values of 'a', 'b', and 'c', Semi perimeter (s) = (6 + 7 + 9)/2 = 22/2 = 11 units.
Now, let us find the area of the triangle using Heron's formula, Area of triangle = √[s(s-a)(s-b)(s-c)]
Substituting the values in the formula, where 's' = 11 units, a = 6 units, 'b' = 7 units, and 'c' = 9 units
Area of triangle = √[s(s-a)(s-b)(s-c)]
Area = √[11(11-6)(11-7)(11-9)] = √[11 × 5 × 4 × 2] = √440= 20.97 square units
Examples on Semi Perimeter of Triangle
-
Example 1: Find the semi perimeter of a triangle with sides 15 units, 13 units, and 14 units.
Solution: The sides of the triangle are given as 'a' = 15 units, 'b' = 13 units, and 'c' = 14 units
We will use the formula for the semi perimeter of triangle, s = (a + b + c)/2
Substituting the values of 'a', 'b', and 'c', Semi perimeter (s) = (15 + 13 + 14)/2 = 42/2 = 21 units.
Answer: The semi perimeter of the triangle is 21 units. -
Example 2: Find the semi perimeter of an equilateral triangle that has a side length of 16 units.
Solution:
Since it is an equilateral triangle, all the three sides are of equal measure. This means the value of the sides of the triangle can be written as: 'a' = 16 units, 'b' = 16 units, and 'c' = 16 units
We will use the formula for the semi perimeter of triangle, s = (a + b + c)/2
Substituting the values of 'a', 'b', and 'c', Semi perimeter (s) = (16 + 16 + 16)/2 = 48/2 = 24 units.
Answer: Therefore, the semi perimeter of the equilateral triangle is 24 units.

FAQs on Semi Perimeter of Triangle
What is the Semi Perimeter of a Triangle?
The semi perimeter of a triangle is half the perimeter of a triangle. 'Semi' means half, that is why the semi perimeter of a triangle is half the value of the perimeter. The semi perimeter of triangle is expressed in linear units like inches, yards, centimeters, and so on.
How to Find the Semi Perimeter of Triangle?
The semi perimeter of a triangle can be calculated by dividing the perimeter of the triangle by 2. In other words, if the lengths of all the sides of a triangle are given, we can calculate the semi perimeter by adding the sides and dividing the sum by 2. The formula that is used to find the semi perimeter of triangle is, Semi perimeter = (a + b + c)/2, where 'a', 'b', 'c' are the three sides of the triangle. For example, if the sides of a triangle are given as 4 units, 8 units, and 6 units, the semi perimeter can be calculated in the following way. Semi perimeter = (4 + 8 + 6)/2 = 18/2 = 9 units.
Where is the Semi Perimeter of Triangle Used?
The semi perimeter of a triangle is used to find the area of triangles using Heron's formula when the length of all three sides is given. The Heron's formula is expressed as, √[s(s-a)(s-b)(s-c)], where 's' = Semi Perimeter of triangle; and 'a', 'b', 'c' are the three sides of the triangle. So, after calculating the semi perimeter of triangle, the value of 's' is placed in the Heron's formula along with the other sides. This gives the area of a triangle whose three sides are given.
What is the Formula of the Semi Perimeter of Triangle?
The basic formula that is used to find the semi perimeter of a triangle is: S = (a + b + c)/2, where 'a', 'b', 'c' are the three sides of the triangle.
What is the Semi Perimeter of Triangle with sides 40 cm, 24 cm, 32 cm?
The semi perimeter of a triangle can be calculated if the length of the three sides is given. The formula for the semi perimeter of a triangle is S = (a + b + c)/2, where 'a', 'b', 'c' are the three sides of the triangle. In this case, 'a' = 40 cm, 'b' = 24 cm, and 'c' = 32 cm. So, we will substitute the values in the formula, S = (a + b + c)/2 = (40 + 24 + 32)/2 = 96/2 = 48 cm. Therefore, the semi perimeter of the triangle is 48 cm.
Find the Semi Perimeter of a Triangle if the Sides are 12 units, 22 units, and 15 units.
The formula for the semi perimeter of a triangle is S = (a + b + c)/2, where 'a', 'b', 'c' are the three sides of the triangle. In this case, 'a' = 12 units, 'b' = 22 units, and 'c' = 15 units. So, we will substitute the values in the formula, S = (a + b + c)/2 = (12 + 22 + 15)/2 = 49/2 =24.5 units.
visual curriculum