Surface Area of Frustum
The surface area of frustum is the sum of the areas of all its faces. Before learning the formula for the surface area of frustum, let us recall what is a frustum. When a pyramid or a cone is sliced off by a plane parallel to its base, then a part of the shape with the base is called a frustum. A frustum is also called a truncated shape. From the following figure, we can understand how a frustum of a cone (or a truncated cone) is formed.

| 1. | What Is the Surface Area of Frustum? |
| 2. | Surface Area of Frustum Formula |
| 3. | Surface Area of Frustum of a Cone Formula |
| 4. | FAQs on Surface Area of Frustum |
What Is the Surface Area of Frustum?
The surface area of a frustum is basically the sum of areas of its faces and is measured in square units like the area of any other shape. i.e., it is measured in cm2, m2, in2, etc. There are two types of surface areas with respect to the frustum.
- Curved Surface Area (CSA) for the frustum of a cone [OR] Lateral Surface Area (LSA) for the frustum of a pyramid.
- Total Surface Area (TSA) for the frustum of a cone (or) the frustum of a pyramid.
The curved surface area of a frustum of a cone is the area of its curved face. The lateral surface area of a frustum of a pyramid is the sum of the areas of all its side faces. The total surface area of a frustum of a cone or a pyramid is the sum of the areas of all its faces.

Surface Area of Frustum Formula
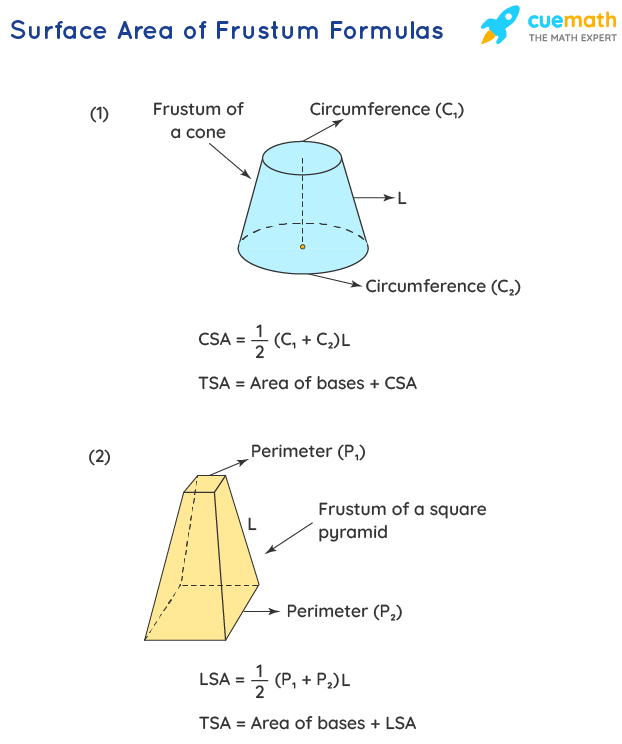
The lateral (or curved) surface area of any frustum can be calculated using the perimeters (or circumferences) of the bases and the slant height. The lateral (or curved) surface area of a frustum is calculated using the formula:
Lateral (or curved) surface area = (1/2) × \((C_1+C_2)\) × L where
- \(C_1\) = The perimeter (or circumference) of one base of the frustum
- \(C_2\) = The perimeter (or circumference) of another base of the frustum
- L = slant height of the frustum
The total surface area of any frustum is obtained by adding the areas of both bases and its lateral (or curved) surface area. i.e.,
Total surface area (TSA) = Area of bases + Lateral (or curved) surface area
Note: Each side face of any frustum of a pyramid is an isosceles trapezoid and thus, the area of each side face can be found by using the area of trapezoid formula (1/2) × (sum of the parallel sides) × (height).
But how to find the surface area of frustum of a cone? Let us see.
Surface Area of Frustum of a Cone Formula
The formula which we learned in the previous section can be used to calculate the surface area of any frustum and hence it can be used to calculate the surface area of the frustum of a cone as well. Consider a cone of height H + h, slant height L + l, and base radius R. Consider the frustum of the cone of height H, a small base radius 'r', a large base radius 'R', and slant height L. Here are the formulas for curved surface area (CSA) and the total surface area (TSA) of a frustum of a circular cone.
The curved surface area (CSA) of the frustum of the cone is,
CSA of frustum of cone = πl [ (R2 - r2) / r ] (OR) πL (R + r)
We know that the base areas of the frustum of the cone are πR2 and πr2. Thus, the sum of base areas is π (R2 + r2). Thus, the total surface area (TSA) of the frustum of the cone is,
TSA of frustum of cone = π (R2 + r2) + πl [ (R2 - r2) / r ] (OR) πL (R + r) + π (R2 + r2)

Note: Here π is a constant whose value is 22/7 (or) 3.141592653...
Here, finding the base areas of the frustum of a cone is very simple. But how to derive the formula(s) for the curved surface area of frustum of cone? We can do this in two methods. Let us see.
Method 1 to Derive the Curved Surface Area of Frustum of a Cone Formula
We will use the surface area of the frustum formula (from the previous section) to derive the surface area of the frustum of a cone. The base circumferences (circumference of circles) of the frustum of the cone from the above figure are:
\(C_1\) = 2πR
\(C_2\) = 2πr
Substituting these values in the curved surface area of frustum formula,
CSA = (1/2) × \((C_1+C_2)\) × L
CSA = (1/2) × (2πR + 2πr) × L
CSA = πL (R + r)
We derived one of the formulas of the surface area of the frustum of the cone in this method. But we can derive both the formulas using the following method.
Method 2 to Derive the Curved Surface Area of Frustum of a Cone Formula
The curved surface area of the full cone is, πR(L + l).
The curved surface area of the cone (with apex) that is cut is, πrl.
We have,
The curved surface area (CSA) of frustum of the cone = The curved surface area of the full cone - The curved surface area of the cone that is cut
CSA = πR (L + l) - πrl... (1)
The triangles OBC and PQC are similar (by AA property of similarity) and thus,
(L + l) / l = R / r ... (2)
L + l = Rl / r ... (3)
Substituting this in (1),
CSA = πR (Rl / r) - πrl
V = πl [ (R2 - r2) / r ]
We derived one formula of the curved surface area of the frustum of the cone. Now we will derive another formula from this.
From (2),
(L / l) + 1 = R / r
L / l = (R / r) - 1
L / l= (R - r) / r
Reciprocating on both sides,
l / L = r / (R - r)
l = (L r) / (R - r)
Substituting this in the above formula,
CSA = (π) [ (L r) / (R - r) ] [ (R2 - r2) / r ]
Using one of the algebraic formulas, a2 - b2 = (a - b) (a + b). By applying this formula to R2 - r2,
CSA = (π ) [ (L r) / (R - r) ] [ (R - r) (R + r) / r ]
CSA = πL (R + r)
Hence, we derived the second formula of the curved surface area of frustum of the cone as well.
Note: The relation between the slant height (L), height (H), and base radii R and r of the frustum of the cone (using the Pythagoras theorem) is, L2 = H2 + (R - r)2. We may need to use this while solving the problems related to the surface area of the frustum of a cone.
Solved Examples on Surface Area of Frustum
-
Example 1: The bases of a frustum of a square pyramid are of lengths 10 units and 7 units. Its slant height is 12 units. Find the total surface area of frustum of the pyramid.
Solution:
The height of the frustum of the square pyramid, L = 12 units.
The perimeters of bases of the frustum are:
\(P_1\) = 4(10) = 40 units.
\(P_2\) = 2(7) = 28 units.
The total surface area of the frustum of the square pyramid is,
TSA = (1/2) × \(P_1+P_2\) × L + Area of bases
TSA = (1/2) × (40 + 28) × 12 + 102 + 72
TSA = 557 square units.
Answer: TSA of the frustum of the square pyramid = 557 square units.
-
Example 2: Find the total surface area of the frustum of a right circular cone of height 20 in, large base radius to be 25 in, and slant height to be 29 in. Express the answer in terms of π.
Solution:
The large base radius of the frustum is, R = 25 in.
Let its small base radius be 'r'.
The height of the frustum of the cone is, H = 20 in.
Its slant height is, L = 29 in.
We know that,
L2 = H2 + (R - r)2
292 = 202 + (25 - r)2
841 = 400 + (25 - r)2
441 = (25 - r)2
Taking square root on both sides,
21 = 25 - r
r = 4
Thus, the total surface area of the given frustum of right circular cone is,
TSA = πL (R + r) + π (R2 + r2)
TSA = π (29) (25 + 4) + π (252 + 42) = 1482π
Answer: The TSA of frustum of the cone = 1482π in2.

FAQs on Surface Area of Frustum
What Is Meant By the Surface Area of Frustum?
We have two types of surface areas of frustum, one is curved (or lateral) surface area which is the area of the curved face (or the sum of the areas of the lateral faces), whereas the other is the total surface area which is the sum of areas of all the faces of the frustum.
What Is the Curved Surface Area of Frustum Formula?
The curved surface area of a frustum of any shape can be calculated by using its height 'H' and its base circumferences \(C_1\) and \(C_2\). The formula to calculate the curved surface area (CSA) of the frustum is,
CSA = (1/2) × \((C_1+C_2)\) × L
What Is the Total Surface Area of the Frustum of a Rectangular Pyramid Formula?
The frustum of a rectangular pyramid is a portion of it that is left after its top portion (with apex) is cut by a plane that is parallel to the base (rectangle). The total surface area of a rectangular pyramid is calculated using the formula: TSA = (1/2) × \((P_1+P_2)\) × L + Area of bases, where
- L = Lateral height of the frustum
- \(P_1\) = The perimeter of the one base rectangle of the frustum
- \(P_2\) = The perimeter of the other base rectangle of the frustum
What Is the Lateral Surface Area of Square Frustum Formula?
The square frustum is a frustum that is formed when a square pyramid's portion (containing apex) is sliced off by a plane that is parallel to the base (square). The lateral surface area of a square frustum is calculated by the formula:
LSA = (1/2) × \((P_1+P_2)\), where
- \(P_1\) = The perimeter of the one base rectangle of the frustum
- \(P_2\) = The perimeter of the other base rectangle of the frustum
- L = Lateral height of the frustum
What Is the Curved Surface Area of the Frustum of a Cone Formula?
There are two formulas that are used to calculate the curved surface area (CSA) of a frustum of a cone. Consider a frustum of radii 'R' and 'r', height 'H', slant height L which is formed by a cone of base radius 'R', height 'H + h', and slant height 'L + l'. Its CSA can be calculated by using:
- πl [ (R2 - r2) / r ] (or)
- πL (R + r)
What Is the Total Surface Area of the Frustum of a Cone Formula?
There are two formulas that are used to calculate the total surface area (TSA) of a frustum of a cone. Consider a frustum of radii 'R' and 'r', height 'H', slant height L which is formed by a cone of base radius 'R', height 'H + h', and slant height 'L + l'. Its TSA can be calculated by using:
- π (R2 + r2) + πl [ (R2 - r2) / r ] (OR)
- πL (R + r) + π (R2 + r2)
What Is the Total Surface Area of the Frustum of a Cone Formula Using Height?
Consider a frustum of radii 'R' and 'r', height 'H', and slant height L which is formed by a cone of base radius 'R', slant height 'L + l', and height 'H + h'. The relation between the height (H), slant height (L), and base radii R and r of the frustum of the cone is, L2 = H2 + (R - r)2. We can use this formula to calculate one of the unknown values among 'r', 'R', and 'H' and then we can find the total surface area of the frustum using the formula πL (R + r) + π (R2 + r2).
visual curriculum