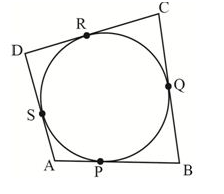
A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC
Solution:
From the given figure we can consider a few points which are as follows:
(i) DR = DS [ As we know that the lengths of the tangents drawn from an external point to the circle are equal.]
(ii) BP = BQ
(iii) AP = AS
(iv) CR = CQ
Since they are tangents on the circle from points D, B, A, and C respectively.
Now let us add both the LHS and RHS of the above equations separately and observing the result.
DR + BP + AP + CR = DS + BQ + AS + CQ
By rearranging the terms we get,
(DR + CR) + (BP + AP) = (CQ + BQ) + (DS + AS)
On further simplifying,
CD + AB = BC + AD
Hence it is proved AB + CD = AD + BC.
☛ Check: NCERT Solutions for Class 10 Maths Chapter 10
Video Solution:
A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC
NCERT Solutions Class 10 Maths Chapter 10 Exercise 10.2 Question 8
Summary:
If a quadrilateral ABCD is drawn to circumscribe a circle, then AB + CD = AD + BC.
☛ Related Questions:
- From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is(A) 7 cm(B) 12 cm(C) 15 cm(D) 24.5 cm
- In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠ POQ = 110°, then ∠ PTQ is equal to(A) 60°(B) 70°(C) 80°(D) 90°
- If tangents PA and PB from a point P to a circle with center O are inclined to each other at angle of 80°, then ∠POA is equal to(A) 50°(B) 60°(C) 70°(D) 80°
- Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
visual curriculum