Fibonacci Sequence
The Fibonacci Sequence is a series of numbers that starts with 0 and 1, and each subsequent number is the sum of the two preceding numbers. So the sequence goes 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. This sequence is named after Leonardo Pica (who was also known as Fibonacci), an Italian mathematician who introduced it to the Western world in his book Liber Abaci in 1202. This sequence has been termed "nature's secret code".
We can spot the Fibonacci sequence in the spiral patterns of sunflowers, daisies, broccoli, cauliflowers, and seashells. Let us learn more about it and its interesting properties.
| 1. | What Is Fibonacci Sequence? |
| 2. | Fibonacci Spiral |
| 3. | Fibonacci Sequence Formula |
| 4. | Fibonacci Sequence Properties |
| 5. | Applications of Fibonacci Sequence |
| 6. | FAQs on Fibonacci Sequence |
What is Fibonacci Sequence?
The Fibonacci sequence is the sequence formed by the infinite terms 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... In simple terms, it is a sequence in which every number in the Fibonacci sequence is the sum of two numbers preceding it in the sequence. Its first two terms are 0 and 1. The terms of this sequence are known as Fibonacci numbers. The first 20 terms of the Fibonacci sequence are given as follows:
| Terms of Fibonacci Sequence | |
|---|---|
| F0 = 0 | F10 = 55 |
| F1 = 1 | F11 = 89 |
| F2 = 1 | F12 = 144 |
| F3 = 2 | F13 = 233 |
| F4 = 3 | F14 = 377 |
| F5 = 5 | F15 = 610 |
| F6 = 8 | F16 = 987 |
| F7 = 13 | F17 = 1597 |
| F8 = 21 | F18 = 2584 |
| F9 = 34 | F19 = 4181 |
Here, we can observe that Fn = Fn-1 + Fn-2 for every n > 1. For example:
- F2 = F1 + F0
- F3 = F2 + F1
- F4 = F3 + F2, and so on.
The significance of the Fibonacci Sequence lies in its prevalence in nature and its applications in various fields, including mathematics, science, art, and finance. The sequence can be observed in the arrangement of leaves on a stem, the branching of trees, and the spiral patterns of shells and galaxies. It is also used to describe growth patterns in populations, stock market trends, and more.
Fibonacci Spiral
The Fibonacci spiral is a geometrical pattern that is derived from the Fibonacci sequence. It is created by drawing a series of connected quarter-circles inside a set of squares that are sized according to the Fibonacci sequence.
The spiral starts with a small square, followed by a larger square that is adjacent to the first square. The next square is sized according to the sum of the two previous squares, and so on. Each quarter-circle fits perfectly within the next square in the sequence, creating a spiral pattern that expands outward infinitely. The larger the numbers in the Fibonacci sequence, the ratio becomes closer to the golden ratio (≈1.618).
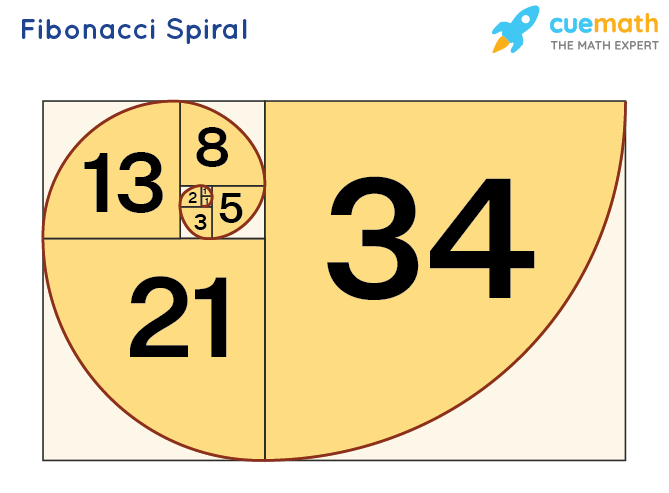
In this Fibonacci spiral, every two consecutive terms of the Fibonacci sequence represent the length and width of a rectangle. Let us calculate the ratio of every two successive terms of the Fibonacci sequence and see how they form the golden ratio.
- F2/F1 = 1/1 = 1
- F3/F2 = 2/1 = 2
- F4/F3 = 3/2 = 1.5
- F5/F4 = 5/3 = 1.667
- F6/F5 = 8/5 = 1.6
- F7/F6 = 13/8 = 1.625
- F8/F7 = 21/13 = 1.615
- F9/F8 = 34/21 = 1.619
- F10/F9 = 55/34 = 1.617
- F11/F10 = 89/55 = 1.618 = Golden Ratio
In this way, when the rectangle is very large, its dimensions are very close to form a golden rectangle.
Overall, the Fibonacci spiral and the golden ratio are fascinating concepts that are closely linked to the Fibonacci Sequence and are found throughout the natural world and in various human creations. Their applications in various fields make them a subject of continued study and exploration.
Fibonacci Sequence Formula
The Fibonacci sequence formula for “Fn” is defined using the recursive formula by setting F0 = 0, F1 = 1, and using the formula below to find Fn. The Fibonacci formula is given as follows.
Fn = Fn-1 + Fn-2, where n > 1. Here
- Fn represents the (n+1)th number in the sequence and
- Fn-1 and Fn-2 represent the two preceding numbers in the sequence.
The Fibonacci sequence formula is used to compute the terms of the sequence to obtain a new term. For example, since we know the first two terms of Fibonacci sequence are 0 and 1, the 3rd term is obtained by the above formula as follows:
F3 = F1 + F2 = 0 + 1 = 1.
In the same way, the other terms of the Fibonacci sequence using the above formula can be computed as shown in the figure below.
Note that F0 is termed as the first term here (but NOT F1). Thus, Fn represents the (n + 1)th term of the Fibonacci sequence here.
Fibonacci Sequence Properties
The Fibonacci sequence has several interesting properties.
1) Fibonacci numbers are related to the golden ratio. Any Fibonacci number can be calculated (approximately) using the golden ratio, Fn =(Φn - (1-Φ)n)/√5 (which is commonly known as "Binet formula"), Here φ is the golden ratio and Φ ≈ 1.618034.
To find the F7, we apply F7 = [(1.618034)7 - (1-1.618034)7] / √5 = 13
2) The ratio of successive terms in the Fibonacci sequence converges to the golden ratio as the terms get larger.
| A | B | A/B |
|---|---|---|
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6 |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
| 144 | 233 | 1.618055555555556 |
| 233 | 377 | 1.618025751072961 |
Just by multiplying the previous Fibonacci Number by the golden ratio (1.618034), we get the approximated Fibonacci number. For example, 13 is a number in the sequence, and 13 × 1.618034... = 21.034442. This gives the next Fibonacci number 21 after 13 in the sequence.
2) Observe the sequence to find another interesting pattern. Every 3rd number in the sequence (starting from 2) is a multiple of 2. Every 4th number in the sequence (starting from 3) is a multiple of 3 and every 5th number (starting from 5) is a multiple of 5; and so on.
3) The Fibonacci sequence works below zero too. We write F-n = (-1)n+1 Fn. For example, F-4 = (-1)5 . F4 = (-1) 3 = -3.
4) The sum of n terms of the Fibonacci sequence is given by Σi=0n Fi = Fn+2 - F2 (or) Fn+2 - 1, where Fn is the nth Fibonacci number. (Note: the first term starts from F0)
For example, the sum of first 10 terms of sequence = 12th term - 1 = 89 - 1 = 88. It can be mathematically written as Σi=09 Fi = F11 - 1 = 89 - 1 = 88.
5) The Fibonacci Sequence has connections to other mathematical concepts, such as the Lucas numbers and Pascal's triangle.
Applications of Fibonacci Sequence
The Fibonacci sequence can be found in a varied number of fields from nature, to music, and to the human body.
- used in the grouping of numbers and the brilliant proportion in music generally.
- used in Coding (computer algorithms, interconnecting parallel, and distributed systems)
- in numerous fields of science including high-energy physical science, quantum mechanics, Cryptography, etc.
- used to model various phenomena in biology, such as the growth patterns of plants and the arrangement of leaves on a stem.
- used in financial analysis to identify trends in stock prices and other financial data.
You can use the Fibonacci calculator that helps to calculate the Fibonacci Sequence. Look at a few solved examples to understand the Fibonacci formula better.
☛ Related Articles:
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
FAQs on Fibonacci Sequence
What is the Definition of Fibonacci Sequence?
The Fibonacci sequence is an infinite sequence in which every number in the sequence is the sum of two numbers preceding it in the sequence and is given by 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 , 144, ..... The ratio of consecutive numbers in the Fibonacci sequence approaches the golden ratio, a mathematical concept that has been used in art, architecture, and design for centuries. This sequence also has practical applications in computer algorithms, cryptography, and data compression.
What is the Formula for Generating the Fibonacci Sequence?
The Fibonacci sequence formula deals with the Fibonacci sequence, finding its missing terms. The Fibonacci formula is given as, Fn = Fn-1 + Fn-2, where n > 1. It is used to generate a term of the sequence by adding its previous two terms.
What is the Difference Between Fibonacci Sequence Formula and Fibonacci Series Formula?
| Fibonacci Sequence Formula | Fibonacci Series Formula |
|---|---|
| The formula calculates a single Fibonacci number in the Fibonacci sequence. | The formula calculates the sum of a range of Fibonacci numbers. |
| F(n) = F(n-1) + F(n-2), with F(0) = 0 and F(1) = 1. | F(n) = F(1) + F(2) + ... + F(n-1) with F(0) = 0 and F(1) = 1. |
| Example: F(5) = F(4) + F(3) = 3 + 2 = 5. | Example: F(5) = F(1) + F(2) + F(3) + F(4) = 1 + 1 + 2 + 3 = 7. |
What is Fibonacci Spiral?
Here are the steps of formation of Fibonacci spiral.
- First, take a small square of length 1 unit and attach it to an identical square vertically.
- Thus formed is a rectangle of vertical length 2 and width 1 unit.
- Adjacent to its length (2 units), attach a square of length 2 units.
- Thus formed is a rectangle of horizontal length 3 units and vertical width 2 units.
- If we continue the same process we get a big rectangle that is partitioned into squares where the length of each square is the sum of the lengths of two of its adjacent squares.
- The larger the rectangle, the more the chances for it to become a golden rectangle.
- If we join the centers of all squares, we get a spiral which is known as the Fibonacci spiral. For more information, click here.
What is The Fibonacci Sequence in Nature?
We can spot the Fibonacci sequence as spirals in the petals of certain flowers, or the flower heads as in sunflowers, broccoli, tree trunks, seashells, pineapples, and pine cones. The spirals from the center to the outside edge create the Fibonacci sequence.
How is the Fibonacci Sequence Related to the Golden Ratio?
The Fibonacci Sequence is closely related to the Golden Ratio, which is a mathematical ratio represented by the symbol phi (φ). The Golden Ratio is approximately equal to 1.61803398875. The ratio of each consecutive pair of Fibonacci numbers approximates the Golden Ratio as the numbers get higher. For example 21/13 = 1.615..., 34/21 = 1.619, ...
How Do You Find the Sum of The Fibonacci Sequence of n Terms?
The explicit formula to find the sum of the Fibonacci sequence of n terms is given by of the given generating function is the coefficient of Σi=0n Fi = Fn+2 - 1. For example, the sum of the first 12 terms in a Fibonacci sequence is Σi=011 Fi = F13 -1 = 233 -1 = 232. If we add the first 12 terms manually, we get 0 + 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 + 89 = 232, we got the same thing as the formula.
What is the Recursive Formula to Find the nth Term of the Fibonacci Sequence?
We can't write a Fibonacci sequence easily using an explicit formula. Thus, we used to describe the sequence using a recursive formula, defining the terms of a sequence using previous terms. When F0 = 0, F1= 1, Fn = Fn-1 + Fn-2, where n > 1.
What is the Formula for the nth Term of The Fibonacci Sequence?
The formula to find the nth term of the sequence is denoted as Fn = Fn-1 + Fn-2, where n >1.
Why is Fibonacci Sequence Important?
The Fibonacci sequence has many interesting mathematical properties, including the fact that the ratio of each consecutive pair of numbers approximates the Golden Ratio. It is also closely related to other mathematical concepts, such as the Lucas Sequence and the Pell Sequence. The Fibonacci sequence has many applications in science and engineering, including the analysis of population growth. The Fibonacci sequence appears in many forms in nature, including the branching of trees.