A day full of math games & activities. Find one near you.

Cube Root of 30

The value of the cube root of 30 rounded to 4 decimal places is 3.1072. It is the real solution of the equation x³ = 30. The cube root of 30 is expressed as ∛30 in the radical form and as (30)^⅓ or (30)^0.33 in the exponent form. The prime factorization of 30 is 2 × 3 × 5, hence, the cube root of 30 in its lowest radical form is expressed as ∛30.

Cube root of 30: 3.107232506
Cube root of 30 in Exponential Form: (30)^⅓
Cube root of 30 in Radical Form: ∛30

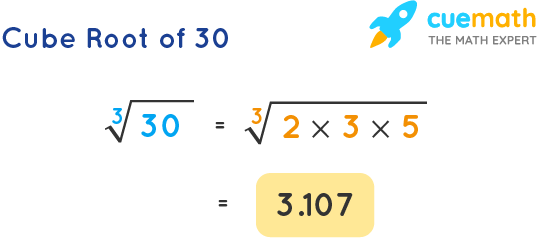
1.	What is the Cube Root of 30?
2.	How to Calculate the Cube Root of 30?
3.	Is the Cube Root of 30 Irrational?
4.	FAQs on Cube Root of 30

What is the Cube Root of 30?

The cube root of 30 is the number which when multiplied by itself three times gives the product as 30. Since 30 can be expressed as 2 × 3 × 5. Therefore, the cube root of 30 = ∛(2 × 3 × 5) = 3.1072.

☛ Check: Cube Root Calculator

How to Calculate the Value of the Cube Root of 30?

Cube Root of 30 by Halley's Method

Its formula is ∛a ≈ x ((x³ + 2a)/(2x³ + a))
where,
a = number whose cube root is being calculated
x = integer guess of its cube root.

Here a = 30
Let us assume x as 3
[∵ 3³ = 27 and 27 is the nearest perfect cube that is less than 30]
⇒ x = 3
Therefore,
∛30 = 3 (3³ + 2 × 30)/(2 × 3³ + 30)) = 3.11
⇒ ∛30 ≈ 3.11
Therefore, the cube root of 30 is 3.11 approximately.

Is the Cube Root of 30 Irrational?

Yes, because ∛30 = ∛(2 × 3 × 5) and it cannot be expressed in the form of p/q where q ≠ 0. Therefore, the value of the cube root of 30 is an irrational number.

☛ Also Check:

Cube Root of 30 Solved Examples

Example 1: Given the volume of a cube is 30 in³. Find the length of the side of the cube.

Solution:

Volume of the Cube = 30 in³ = a³
⇒ a³ = 30
Cube rooting on both sides,
⇒ a = ∛30 in
Since the cube root of 30 is 3.11, therefore, the length of the side of the cube is 3.11 in.
Example 2: What is the value of ∛30 + ∛(-30)?

Solution:

The cube root of -30 is equal to the negative of the cube root of 30.
i.e. ∛-30 = -∛30

Therefore, ∛30 + ∛(-30) = ∛30 - ∛30 = 0
Example 3: The volume of a spherical ball is 30π in³. What is the radius of this ball?

Solution:

Volume of the spherical ball = 30π in³
= 4/3 × π × R³
⇒ R³ = 3/4 × 30
⇒ R = ∛(3/4 × 30) = ∛(3/4) × ∛30 = 0.90856 × 3.10723 (∵ ∛(3/4) = 0.90856 and ∛30 = 3.10723)
⇒ R = 2.8231 in³

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on Cube Root of 30

What is the Value of the Cube Root of 30?

We can express 30 as 2 × 3 × 5 i.e. ∛30 = ∛(2 × 3 × 5) = 3.10723. Therefore, the value of the cube root of 30 is 3.10723.

What is the Cube of the Cube Root of 30?

The cube of the cube root of 30 is the number 30 itself i.e. (∛30)³ = (30^1/3)³ = 30.

What is the Value of 16 Plus 3 Cube Root 30?

The value of ∛30 is 3.107. So, 16 + 3 × ∛30 = 16 + 3 × 3.107 = 25.321. Hence, the value of 16 plus 3 cube root 30 is 25.321.

Is 30 a Perfect Cube?

The number 30 on prime factorization gives 2 × 3 × 5. Here, the prime factor 2 is not in the power of 3. Therefore the cube root of 30 is irrational, hence 30 is not a perfect cube.

How to Simplify the Cube Root of 30/8?

We know that the cube root of 30 is 3.10723 and the cube root of 8 is 2. Therefore, ∛(30/8) = (∛30)/(∛8) = 3.107/2 = 1.5535.

If the Cube Root of 30 is 3.11, Find the Value of ∛0.03.

Let us represent ∛0.03 in p/q form i.e. ∛(30/1000) = 3.11/10 = 0.31. Hence, the value of ∛0.03 = 0.31.