A day full of math games & activities. Find one near you.

Cube Root of 64

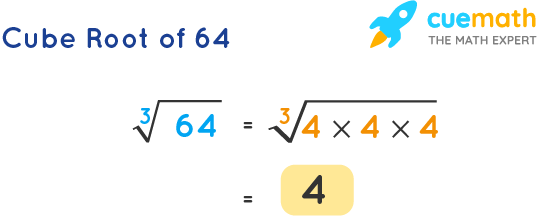
The value of the cube root of 64 is 4. It is the real solution of the equation x³ = 64. The cube root of 64 is expressed as ∛64 in radical form and as (64)^⅓ or (64)^0.33 in the exponent form. As the cube root of 64 is a whole number, 64 is a perfect cube.

Cube root of 64: 4
Cube root of 64 in exponential form: (64)^⅓
Cube root of 64 in radical form: ∛64

Cube Root of 64

1.	What is the Cube Root of 64?
2.	How to Calculate the Cube Root of 64?
3.	Is the Cube Root of 64 Irrational?
4.	FAQs on Cube Root of 64

What is the Cube Root of 64?

The cube root of 64 is the number which when multiplied by itself three times gives the product as 64. Since 64 can be expressed as 2 × 2 × 2 × 2 × 2 × 2. Therefore, the cube root of 64 = ∛(2 × 2 × 2 × 2 × 2 × 2) = 4.

How to Calculate the Value of the Cube Root of 64?

In this section, we will learn how to calculate the cube root of 64 step-wise.

Cube Root of 64 by Prime Factorization

Step 1: Determine the prime factorization of 64 i.e. 64 = 2 × 2 × 2 × 2 × 2 × 2
Step 2: Group the prime factors of 64 in groups of three each. 64 = (2 × 2 × 2) × (2 × 2 × 2) = 2³ × 2³
Step 3: Use the law of exponents: 64 = 2³ × 2³ = 4³
Step 4: Take the cube root on both sides of the equation.

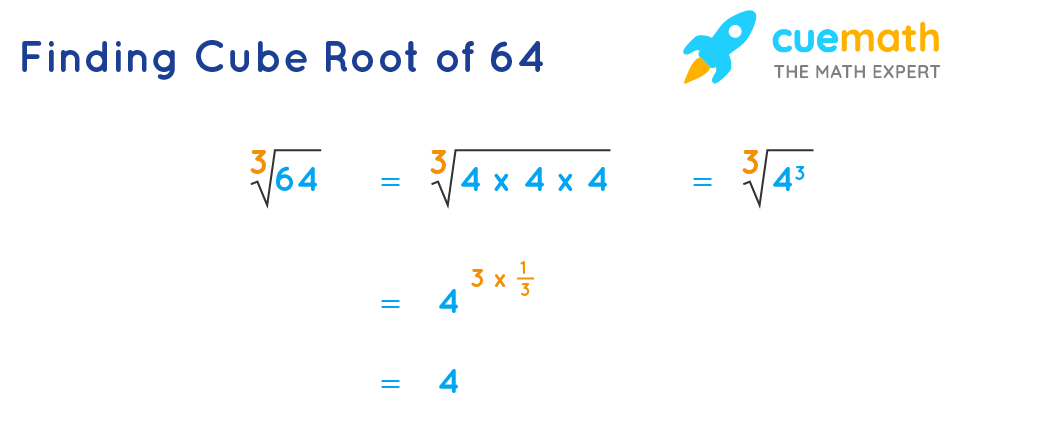
How to Find Cube Root of 64 by Prime Factorization

Therefore, the cube root of 64 by prime factorization is (2 × 2 × 2 × 2 × 2 × 2)^1/3 = 4.

Is the Cube Root of 64 Irrational?

No, because ∛64 = ∛(2 × 2 × 2 × 2 × 2 × 2) can be expressed in the form of p/q i.e. 4/1. Therefore, the value of the cube root of 64 is an integer (rational).

☛ Also Check:

Cube Root of 64 Solved Examples

Example 1: Find the real root of the equation x³ − 64 = 0.

Solution:

x³ − 64 = 0 i.e. x³ = 64
Solving for x gives us,
x = ∛64, x = ∛64 × (-1 + √3i))/2 and x = ∛64 × (-1 - √3i))/2
where i is called the imaginary unit and is equal to √-1.
Ignoring imaginary roots,
x = ∛64
Therefore, the real root of the equation x³ − 64 = 0 is for x = ∛64 = 4.
Example 2: The volume of a spherical ball is 64π in³. What is the radius of this ball?

Solution:

Volume of the spherical ball = 64π in³
= 4/3 × π × R³
⇒ R³ = 3/4 × 64
⇒ R = ∛(3/4 × 64) = ∛(3/4) × ∛64 = 0.90856 × 4 (∵ ∛(3/4) = 0.90856 and ∛64 = 4)
⇒ R = 3.63424 in³
Example 3: What is the value of ∛64 ÷ ∛(-64)?

Solution:

The cube root of -64 is equal to the negative of the cube root of 64.
⇒ ∛-64 = -∛64

Therefore,
⇒ ∛64/∛(-64) = ∛64/(-∛64) = -1

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on Cube Root of 64

What is the Value of the Cube Root of 64?

We can express 64 as 2 × 2 × 2 × 2 × 2 × 2 i.e. ∛64 = ∛(2 × 2 × 2 × 2 × 2 × 2) = 4. Therefore, the value of the cube root of 64 is 4.

How to Simplify the Cube Root of 64/125?

We know that the cube root of 64 is 4 and the cube root of 125 is 5. Therefore, ∛(64/125) = (∛64)/(∛125) = 4/5 = 0.8.

Is 64 a Perfect Cube?

The number 64 on prime factorization gives 2 × 2 × 2 × 2 × 2 × 2. Combining the prime factors in groups of 3 gives 4. So, the cube root of 64 = ∛(2 × 2 × 2 × 2 × 2 × 2) = 4 (perfect cube).

If the Cube Root of 64 is 4, Find the Value of ∛0.064.

Let us represent ∛0.064 in p/q form i.e. ∛(64/1000) = 4/10 = 0.4. Hence, the value of ∛0.064 = 0.4.

Why is the Value of the Cube Root of 64 Rational?

The value of the cube root of 64 can be expressed in the form of p/q i.e. = 4/1, where q ≠ 0. Therefore, the ∛64 is rational.

What is the Value of Cube Root of -64?

We know that the cube root of negative numbers is negative.

Write -64 as a product of its prime factors: -64= -(2 × 2 × 2 × 2 × 2 × 2)
Club the factors into groups of three each: -64= -2³× 2³ = -4³
Take the cube root on both sides of the equation: ³√-64 = ³√-4³= -4

Hence, the cube root of -64 is -4.

Find if Cube Root of 64 Minus Cube Root of 8 is a Rational Number?

The value of cube root of 64 and 8 is 4 and 2 respectively i.e. ³√64 - ³√8 = 4 - 2 = 2. Hence, the difference between the cube root of 64 and the cube root of 8 is a rational number.

What is the Cube of the Cube Root of 64?

The cube of the cube root of 64 is the number 64 itself i.e. (∛64)³ = (64^1/3)³ = 64.

Math worksheets and
visual curriculum