Importance of Coefficients in Polynomials

In any polynomial, the coefficients play a crucial role in determining its characteristics. Let’s see the role of coefficients in determining what kind of graph a linear polynomial will have. Consider the following linear polynomial:

\[a\left( x \right):  mx + b\]

The two coefficients in this polynomial are m and b. How are their values linked to the graph of the polynomial? To understand that, let us first fix the value of b, and vary the value of m. Let us fix b equal to 1, and let us give three different values to m: 1, 2 and 5. The following figure shows (on the same graph) the three lines we will obtain:

What do we observe? Increasing the value of m increases the steepness or slope of the line. In fact, when a linear polynomial is expressed as \(mx + b\), the parameter m is called the slope of the line. Clearly, the value of m is strongly related with the graph of the corresponding linear polynomial.

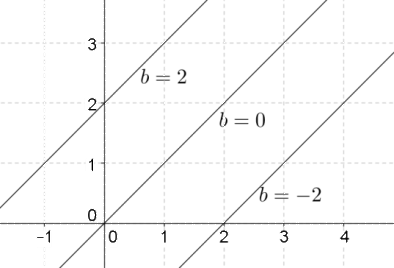
Now, let’s see the role of b. Let us now fix the value of m at 1, and give three different values to b: –2, 0 and 2. The following figure shows (once again on the same graph) the three lines we will obtain:

What do we observe in this case? Increasing the value of b shifts the line upward, while not having any effect on the steepness of the line. When a linear polynomial is expressed as mx + b, the parameter b is called the y-intercept, since it determines where the line will intersect the y axis. In other words, it determines the vertical positioning of the line.

Clearly, the coefficients in a linear polynomial mx + b have a strong correlation with its graph. The zero of a linear polynomial mx + b is also decided by the coefficients:

\[x =  - \frac{b}{m}\]

Here is another example. The following figure shows the curves corresponding to three different quadratic polynomials. Once again, note how the coefficients determine the position of the curve, its spread, and whether it opens upward or downward:

The graph above indicates that if the coefficient of the square term is negative in a quadratic polynomial, the corresponding curve will open downward.

Example 1: In the following figure, three lines marked A, B and C are shown:

Which of the three lines has the highest slope, and which has the highest y intercept?

Solution: The line C seems to be the steepest. However, from a lower class, you already know that a line oriented this way will have a negative slope. In fact, the equation of line C is:

\[y =  - 3x + 2.5\]

Can you deduce this from the graph? Now, among A and B, line A is steeper. Thus, we can say that line A has the highest slope.

The y intercept is highest for line C, since its intersection point with the y axis is the topmost.

Example 2: Three linear polynomials are defined as follows:

\[\begin{array}{l}a\left( x \right): &  - px + 7\\b\left( x \right): & qx + 3\\c\left( x \right): & rx - 2\end{array}\]

p, q and r are variables. Among the three lines corresponding to these equations, which line will intersect the y axis at the lowermost point?

Solution: The y intercept is lowest for the third polynomial, and hence the third line will intersect the y axis at the lowermost point. Note that the values of p, q and r have no effect whatsoever on the y intercepts. Those values will only control the steepness of the lines, and not their vertical positioning.