When a certain number of things are divided into groups with an equal number of things in each group, the number of leftover things is known as the remainder.
It is something that "remains" after division.
Let us consider an example.
Assume that you have 15 cookies that you want to share with 3 of your friends, Mary, David, and Jake.
You want to share the cookies equally among your friends and yourself.
You begin distributing them in the following way (shown in the image).
Here, you can see that there are 3 cookies remaining after the distribution.
These 3 cookies cannot be further shared equally among the 4 of you.
Hence, 3 is called the remainder here.
With this, we learned about the basics of the remainder. Learning the concept of the remainder theorem will now come easily to us.
In this mini-lesson, we explore the world of the remainder theorem. We walk through answers to questions like what is remainder theorem, formula of remainder theorem, and how does remainder theorem work, along with solved examples and interactive questions.
Lesson Plan
What is the Remainder Theorem?
The remainder theorem is stated as follows: When a polynomial a(x) is divided by a linear polynomial b(x) whose zero is x = k, the remainder is given by r = a(k).
The remainder theorem enables us to calculate the remainder of the division of any polynomial by a linear polynomial, without actually carrying out the steps of the division algorithm.
What Is Remainder Theorem Formula?
Remainder Theorem Formula
The general formula for remainder theorem is
| p(x) = (x-c)·q(x) + r(x) |
Let us consider polynomials to prove the remainder theorem formula.
You know that Dividend = (Divisor × Quotient) + Remainder
If r(x) is the constant then, p(x) = (x-c)·q(x) + r
Let us put x=c
p(c) = (c-c)·q(c) + r
p(c) = (0)·q(c) + r
p(c) = r
Hence, proved.
How Does Remainder Theorem Work?
To understand how the remainder theorem works, let us consider a general case. Let a(x) be the dividend polynomial and b(x) the linear divisor polynomial, and let q(x) be the quotient and r the constant remainder. Thus, we have
a(x) = b(x) q(x) + r
Let us denote the zero of the linear polynomial b(x) by k. This means that
b(k) = 0
If we plug in x as k in the starred relation above, we have
a(k) = b(k) q(k) + r
Note that doing this is allowed since the starred relation holds true for every value of x. In fact, it is a polynomial identity. Since b(k)=0 we are left with a(k)=r.
In other words, the remainder is equal to the value of a(x) when x is equal to k. Precisely what we stumbled upon!
This is exactly what the remainder theorem is: When a polynomial a(x) is divided by a linear polynomial b(x) whose zero is x equal to k, the remainder is given by r=a(k).
To see how it works in the case of polynomials, let us consider the following example with two polynomials:
a(x) : 6x4 - x3 + 2x2 - 7x + 2
b(x) : 2x + 3
On dividing polynomials, the quotient polynomial and the remainder are:
q(x) = 3x3 - 5x2 + 17/2 x - 65/4 r = 203/4
We calculated the remainder in this case to be r = 203/4. Now, let’s see what happens when we evaluate a(x) for x equal to the zero of b(x), which is x = -3/2. We have
Once again, this has turned out to be equal to the remainder we calculated using the division algorithm.
- When a polynomial a(x) is divided by a linear polynomial b(x) whose zero is x = k, the remainder is given by r = a(k)
- The remainder theorem formula is: p(x) = (x-c)·q(x) + r(x).
- The basic formula to check the division is: Dividend = (Divisor × Quotient) + Remainder
Solved Examples
Let us have a look at solved examples on the remainder theorem.
| Example 1 |
Casey is solving a polynomial expression. Help her find the remainder when p(x):3x5−x4+x3−4x2+2 is divided by q(x):x−1.
Solution
We will use the remainder theorem: we will substitute the zero of q(x) into the polynomial p(x) to find the remainder r:
r = p(1)
= 3(1)5 - (1)4 + (1)3 - 4(1)2 + 2
= 3 - 1 + 1 - 4 + 2
= 1
| Example 2 |
Consider the following polynomial:
p(x): x6−2x5+x4+2x3+x2−36
Evaluate the value of this polynomial when x is equal to 2. What can you infer from your answer?
Solution
We have
p(2) = (2)6 − 2(2)5 + (2)2 + 2(2)3 + (2)2 − 36
= 64 – 64 + 16 + 16 + 4 − 36
= 0
This means that if p(x) is divided by the linear polynomial q(x) : x - 2 there will be no remainder! Thus, we can conclude that q(x) is a factor of p(x).
In general, whenever a polynomial is divided by a linear divisor and the remainder is 0, the linear divisor must be a factor of the polynomial.
| Example 3 |
Consider the following two polynomials:
a(x) : x3−x2+x−1
b(x) : 2x+1
Find the remainder polynomial and the quotient when a(x) is divided by b(x).
Solution
We proceed as earlier:
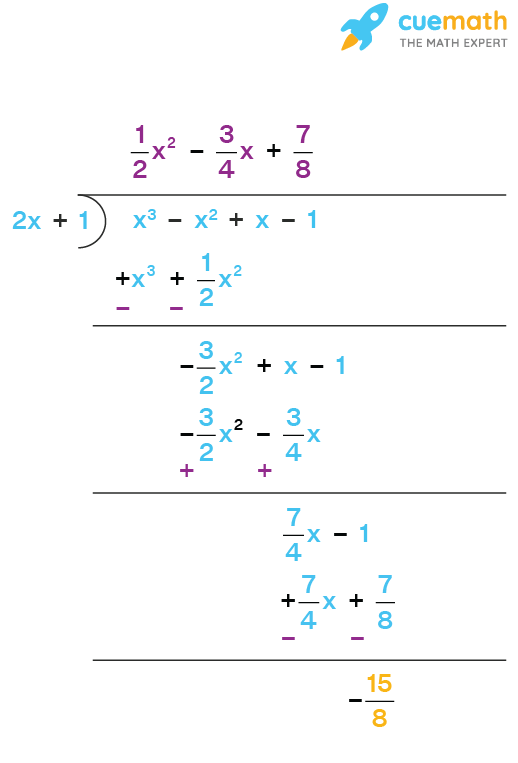
Thus, we have
q(x): 1/2x2 - 3/4x + 7/8
r = -15/8
Let us try to find the same using the remainder theorem.
Putting \(x=-1/2\) in \(x^3-x^2+x-1\)
we have,
=(-1/2)3- (-1/2)2 + (-1/2) -1
=(-1/8) - (1/4) - (1/2) -1
= -7/8 - 1
= -15/8
| \(\therefore\) R= -15/8 |
Interactive Question
Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.
Find the remainder when \(\begin{align}x^{3}+3 x^{2}+3 x+1\end{align}\) is divided by
(i) \(\begin{align} x+1 \end{align}\)
(ii) \(\begin{align} x-\frac{1}{2}\end{align}\)
(iii) \(\begin{align} x\end{align}\)
(iv) \(\begin{align} x+\pi\end{align}\)
(v) \(\begin{align}5+2 x \end{align}\)
Let's Summarize
The mini-lesson targeted the fascinating concept of the remainder theorem. The math journey around what are remainder theorem starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that is not only relatable and easy to grasp but will also stay with them forever. Here lies the magic with Cuemath.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.
FAQs on Remainder Theorem
Q1. What is the remainder theorem in math?
The Remainder Theorem enables us to calculate the remainder of the division of any polynomial by a linear polynomial, without actually carrying out the steps of the division algorithm.
When a polynomial a(x) is divided by a linear polynomial b(x) whose zero is x = k, the remainder is given by r = a(k).
Q2. How do you use the remainder theorem?
To see how it works in case of polynomials, let us consider the following example with two polynomials:
Consider the following two polynomials:
a(x) : x3−x2+x−1
b(x) : 2x+1
Putting \(x=-1/2\) in \(x^3-x^2+x-1\)
we have
=(-1/2)3- (-1/2)2 + (-1/2) -1
=(-1/8) - (1/4) - (1/2) -1
= -7/8 - 1
= -15/8
Q3. Are factor theorem and remainder theorem same?
The factor theorem says that given a polynomial a(x), if its value at x equal to some real number k is equal to 0, that is, if a(k)=0, then the linear polynomial (x - k) is a factor of a(x), and we can write a(x) = (x-k) b(x) where b(x) is a polynomial of degree one less than a(x).
Q4. What is the remainder theorem formula?
The general formula for remainder therem is,
p(x) = (x-c)·q(x) + r(x)
Let us consider polynomials to prove remainder theorem formula.
You know that Dividend = (Divisor × Quotient) + Remainder
If r(x) is the constant then, p(x) = (x-c)·q(x) + r
Let us put x=c
p(c) = (c-c)·q(c) + r
p(c) = (0)·q(c) + r
p(c) = r
Hence, proved.
Q5. Who invented the remainder theorem?
Chinese mathematician Sun Zi invented the remainder theorem. The complete remainder theorem was given by Qin Jiushao in 1247.
Q6. What if the remainder is zero?
If the remainder is zero, then the remaining quotient and the divisor are the factors of the given expression.
Q7. What is the use of the factor theorem?
Factor theorem is used in math to find the factors of a given polynomial equation.
Let say hypothetically, if f(x) is a polynomial, putting f(k) = 0, then (x – k) is a factor of f(x).