A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
LearnPracticeDownload

Square Root of 31

The square root of 31 is a number which, when multiplied by itself, results in the number 31. 31 is also a prime number which makes it trickier to calculate its square root. We will learn how to calculate the square root of 31 and look at a few problems to help us understand this topic.

Square Root of 31: √31= 5.56776436...
Square of 31: 312 = 961

1. What Is the Square Root of 31?
2. Is Square Root of 31 Rational or Irrational?
3. How to Find the Square Root of 31?
4. Challenging Questions
5. Important Notes
6. FAQs on Square Root of 31

What Is the Square Root of 31?

The square root of a number is a number which, when multiplied by itself, results in the original number. For example, the square root of 25 is 5, as 5 times 5 results in 25 which makes it a perfect square. However, you can also have square roots of some numbers that do not result in whole numbers, such as 31. We can express the square root of 31 in different ways:

  • Decimal form: 5.568
  • Radical form: √31
  • Exponent form: 311/2

Is the Square Root of 31 Rational or Irrational?

  • The decimal part of the square root of 31 is non-terminating. This is the definition of an irrational number. 
  • Looking at the decimal form of the root of 31. We can observe that it is never-ending.
    √31= 5.56776436…….
  • Therefore, we can conclude that the square root of 31 is irrational.

How to Find the Square Root of 31?

Since we concluded that the square root of 31 is non-terminating, we can only use two methods to calculate the value of its square root:

  • Long Division Method
  • Estimation and Approximation Method

Long Division Method

  • Step 1: Starting from the right, we will pair up the digits 31 by placing a bar above them. We will also pair the 0s in decimals from left to right.
  • Step 2: Think of a number whose square is less than or equal to 31. In this case, that number would be 5.
  • Step 3: Divide 31 by 5. We will get the quotient as 5 and the remainder as 6. 
  • Step 4: Drag a pair of 0’s down and fill it next to 6 to make the dividend 600. 
  • Step 5: The divisor, in this case 5, is doubled and written below. Now, we have 10X as the new divisor and we need to find a value of X such that the product of 10X × X is less than or equal to 600. In this case, 105 is the required value.
  • Step 6: The number 5 is placed in the quotient after a decimal place. The new divisor for the next division will be 105 + 5, in this case, 110.
    Proceeding in the same manner and repeating from step 4, we can calculate the rest of the decimals.

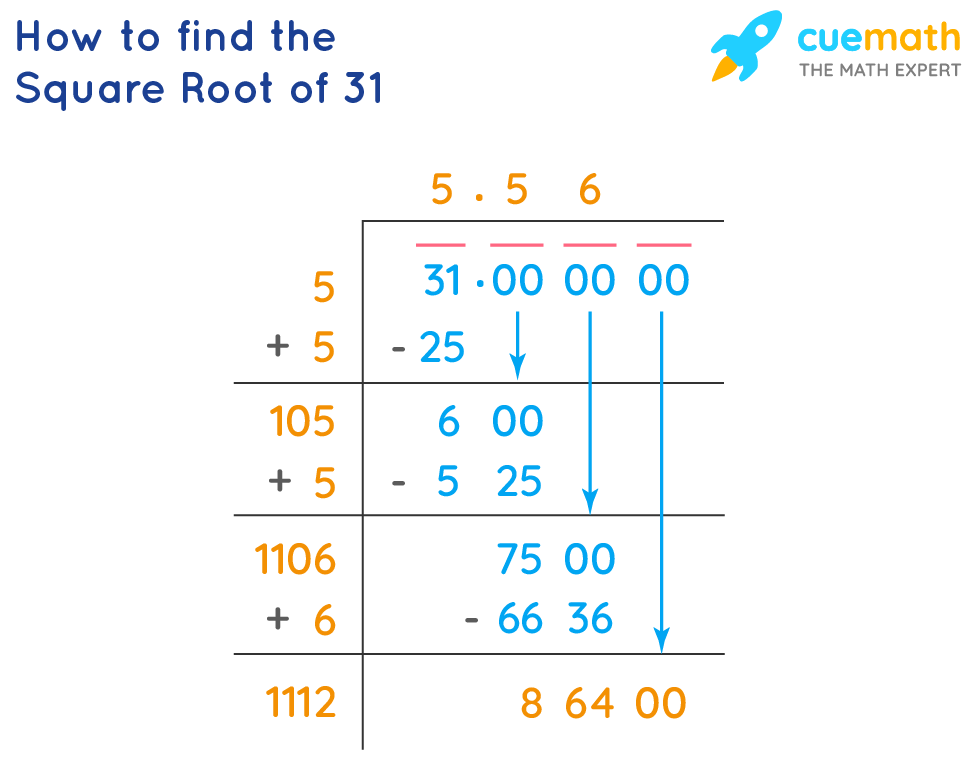
Square Root of 31 by long division method

Therefore, the square root of 31 = 5.567

Estimation and Approximation Method

The estimation method gives us an approximate answer and is usually not accurate to more than 1 decimal place. However, this method is easier to perform.

  • Step 1: Find a perfect square that is smaller than and bigger than 31. In this case, 5 and 6 will work as their squares are 25 and 36.
  • Step 2: Writing in terms of inequality: 52 < √31 < 62 = 25 < 31 < 26
  • Step 3: Multiply by 10 and write in terms of square roots: √2500 < √3100 < √2600
  • Step 4: Move closer to inequality: √3025 < √3100 < √3136 = 55 < 10√31 < 56
    = 5.5 < √31 < 5.6
  • Step 5: Taking average of upper and lower limits we get, (5.5 + 5.6)/2 = 5.55

Therefore, we can estimate the square root of 31 ≅ 5.55

Explore square roots using illustrations and interactive examples

Challenging Questions

  • Find the value of:
    • √0.31
    • √3100
  • What are the roots of -31? Also, find the value of the square of the negative root of -31.

Important Notes

  • The real roots of √31 are ± 5.568.
  • Square root of a perfect square is always a whole number and that of any other number is always irrational. For example, √16 = 4, whereas √17 = 4.1231…
 

Solved Examples

  1. Example 1: Mrs. Becky wants to fence her square garden. The garden has an area of 31 square meters. Find the perimeter of the garden rounded to the nearest hundredth.

    Solution:

    To find the perimeter, we have to calculate the side length.
    Let side length be denoted by s, perimeter by P, and area by A.
    A = s2 or s = √A
    P = 4s = 4 × s = 4√A = 4√31
    P = 4 × 5.568 = 22.272
    Hence, the perimeter of the garden is 22.27 meters.

  2. Example 2: What is the circumference of a circular race track whose area is 31π m2?

    Solution: 

    Let circumference be denoted by C, area by A, and radius length by r.
    C = 2πr
    A = πr2
    31π = πr2
    Simplifying we get, r2 = 31 which implies r = √31
    C = 2πr = 2π × √31 = 34.97 m

    Therefore, the circumference of the track is 34.97 m.

Show Solution >

go to slidego to slide

 

Have questions on basic mathematical concepts?
Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts

Book a Free Trial Class

 

FAQs on Square Root of 31

What is the square root of 31?

The square root of 31 is √31= 5.568.

Is the square root of 31 a rational number?

No, the square root of 31 is not a rational number since the square root of 31 is non-terminating and cannot be represented in the form of p/q.

What is the square root of 31 in the simplest radical form?

√31 is the simplest radical form.

What is the square of 31?

The square of 31 is 312 = 961

Can we find the square root of 31 by the prime factorization method?

No, we can’t find the square root of 31 by the prime factorization method. This is because it is a prime number and its only factors are itself and 1. Therefore, we cannot simplify it further.

Math worksheets and
visual curriculum