External Division

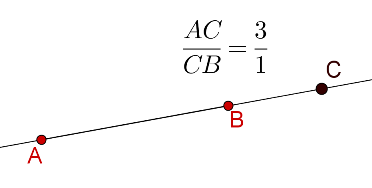
Let us now understand the concept of external division of a line segment. Consider a line segment \(AB\):

We want to find out a point lying on the extended line \(AB\), outside of the segment \(AB\), such that \({\rm{AC:CB  =  3:1}}\) , as shown in the figure below:

We will say that \(C\) externally divides \(AB\) in the ratio 3:1.

✍Note: We can note that the following are different:

• \(C\) divides \(AB\) externally in the ratio 3:1.

• \(C\) divides \(BA\) externally in the ratio 3:1.

In the latter case, \(C\) would be a point on the extended line \(AB\), outside of the segment \(AB\), such that \({\rm{BC:CA  =  3:1}}\), as shown in the figure below:

---

Now, how do we geometrically locate \(C\) if it divides \(AB\) externally in the ratio 3:1. This is similar to the case of internal division, as we once again have to make use of the Basic Proportionality Theorem, in a slightly different manner than earlier. The steps of the construction are outlined below:

• Through \(A\), draw any ray \(AX\), as shown below:

• On \(AX\), mark off 3 equal intervals using a compass:

• Join \(Q\) to \(B\). Through \(R\), draw ray \(RZ\) parallel to \(QB\). The point at which \(RZ\) intersects the extended line \(AB\) is the required point \(C\):

This works because using the BPT, we have \({\rm{AC:CB  =  AR:RQ}}\), but \({\rm{AR:RQ}}\) is 3:1, because \({\rm{AP  =  PQ  =  QR}}\). Thus, \({\rm{AC:CB  =  3:1}}{\rm{.}}\).

✍Note: Please go through Basic Proportionality Theorem to understand it in a better way.

Now, as in the case of internal division, let us revisit this problem of external division from the perspective of coordinates. Suppose that you are given the coordinates of two points \(A\) and \(B\) in the plane.

Think: How can you find the coordinates of a point \(C\) which divides \(AB\) externally in a given ratio? We want to find the coordinates of \(C\), that is, we want an algebraic answer, in terms of the coordinates of \(A\) and \(B\).

---

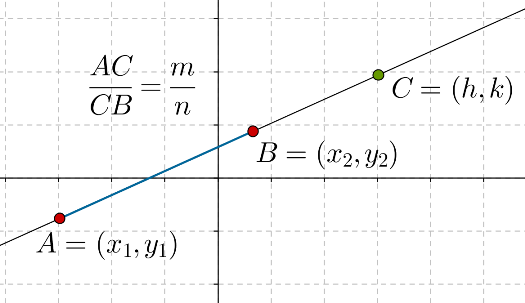
Suppose that the coordinates of \(A\) and \(B\) are:

\[\begin{array}{l}A \equiv \left( {{x_1},\;{y_1}} \right)\\B \equiv \left( {{x_2},\;{y_2}} \right)\end{array}\]

We want to find a point \(C\) which divides \(AB\) externally in the ratio \(m:n\). Let \(C\) be the point \(C \equiv \left( {h,\;k} \right)\). Consider the following figure:

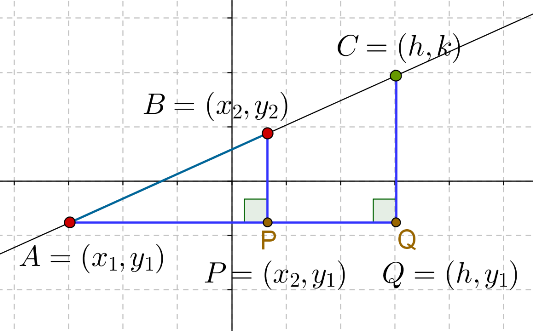
Our problem is to find the coordinates of \(C\) in terms of the coordinates of \(A\) and \(B\), and the parameters \(m\) and \(n\). Let us complete the right triangles, \(\Delta APB\) and \(\Delta AQC\), as shown below:

We note that \(AQ\) and \(AP\) are parallel to the \(x\)-axis, while \(BP\) and \(CQ\) are parallel to the \(y\)-axis, and so:

\[\begin{array}{l}P \equiv \left( {{x_2},\;{y_1}} \right)\\Q \equiv \left( {h,\;{y_1}} \right)\end{array}\]

Now, we make the following observations:

\[\begin{align}&AP = {x_2} - {x_1},\;BP = {y_2} - {y_1}\\&AQ = h - {x_1},\;CQ = k - {y_1}\end{align}\]

Since \({\rm{\Delta APB \sim \  \Delta AQC}}\) , we have:

\[\frac{{AP}}{{AQ}} = \frac{{BP}}{{CQ}} = \frac{{AB}}{{AC}}\;\;\;\;\;\;\;\;\;\; ...({\rm{1}})\]

The next step is the main part in our derivation. We already have the expressions for the terms in the first two ratios above, but what about the third ratio? What is the value of \(AB:AC\)? Since \(C\) divides \(AB\) externally in the ratio \(m:n\), we have:

\[\begin{align}&\frac{{AC}}{{CB}} = \frac{m}{n}\\& \Rightarrow  \;\;\; \frac{{CB}}{{AC}} = \frac{n}{m}\\&\Rightarrow  \;\;\; 1 - \frac{{CB}}{{AC}} = 1 - \frac{n}{m}\\ &\Rightarrow  \;\;\; \frac{{AC - CB}}{{AC}} = \frac{{m - n}}{m}\\& \Rightarrow  \;\;\; \frac{{AB}}{{AC}} = \frac{{m - n}}{m}\end{align}\]

Using this value in (1), we have:

\[\begin{align}&  \frac{{AP}}{{AQ}} = \frac{{BP}}{{CQ}} = \frac{{m - n}}{m}\\& \Rightarrow  \quad \frac{{{x_2} - {x_1}}}{{h - {x_1}}} = \frac{{{y_2} - {y_1}}}{{k - {y_1}}} = \frac{{m - n}}{m}\\ &\Rightarrow  \quad\left\{ \begin{gathered}\frac{{{x_2} - {x_1}}}{{h - {x_1}}} = \frac{{m - n}}{m}\\\frac{{{y_2} - {y_1}}}{{k - {y_1}}} = \frac{{m - n}}{m}\end{gathered} \right.\\ &\Rightarrow  \quad \left\{ \begin{gathered}h - {x_1} = \left( {\frac{m}{{m - n}}} \right)\left( {{x_2} - {x_1}} \right)\\k - {y_1} = \left( {\frac{m}{{m - n}}} \right)\left( {{y_2} - {y_1}} \right)\end{gathered} \right.\\& \Rightarrow \quad \left\{ \begin{gathered}h = {x_1} = \left( {\frac{m}{{m - n}}} \right)\left( {{x_2} - {x_1}} \right)\\k = {y_1} + \left( {\frac{m}{{m - n}}} \right)\left( {{y_2} - {y_1}} \right)\end{gathered} \right. \end{align}\]

\[\Rightarrow  \fbox{$\displaystyle{h = \frac{{m{x_2} - n{x_1}}}{{m -n}},\;k = \frac{{m{y_2} - n{y_1}}}{{m - n}}}$}\]

This is the section formula for external division, and it gives us the coordinates of \(C\) in terms of the coordinates of \(A\) and \(B\), and the parameters \(m\) and \(n\). The only difference between this formula and the one for internal division is that we have negative \(n\) instead of \(n\) in this formula.

✍Note: Please go through Internal Division to understand the difference in a better way.

There is a very important point which must be noted here. The formula above holds for the case when \(C\) divides \(AB\) externally in the ratio \(m:n\). Suppose that \(C\) divides \(BA\) externally in the ratio \(m:n\), that is, \(BC:CA = m:n\). In that case, the coordinates of \(C\) will be (verify this):

\[\boxed{C \equiv \left( {\frac{{m{x_1} - n{x_2}}}{{m - n}},\frac{{m{y_1} - n{y_2}}}{{m - n}}} \right)}\]

Thus, be careful in this regard when you are applying the section formula.

---

Example-1: Consider the following two points:

\[A = \left( { - 2,\;3} \right),B = \left( {2,\; - 1} \right)\]

Find the point which divides \(AB\) externally in the ratio:

• 1:3

• 3:1

Solution: Let

\[C = \left( {{x_C},\;{y_C}} \right),\;D = \left( {{x_D},\;{y_D}} \right)\]

be the points which divide \(AB\) externally in the ratio 1:3 and 3:1 respectively. We now make use of the section formula for external division.

Coordinates of C:

\[\begin{align}&{x_C} = \frac{{\underbrace {\left( {1 \times 2} \right)}_{m{x_2}} - \underbrace {\left( {3 \times - 2} \right)}_{n{x_1}}}}{{\underbrace {1 - 3}_{m - n}}} = \frac{{2 + 6}}{{ - 2}} = - 4\\&{y_C} = \frac{{\underbrace {\left( {1 \times - 1} \right)}_{m{y_2}} - \underbrace {\left( {3 \times 3} \right)}_{n{y_1}}}}{{\underbrace {1 - 3}_{m - n}}}\; = \frac{{ - 1 - 9}}{{ - 2}} = 5\\&\Rightarrow \;\;\;\; \boxed{C = \left( {{x_C},\;{y_C}} \right) = \left( { - 4,\;5} \right)}\end{align}\]

Coordinates of D:

\[\begin{align}&{x_D} = \frac{{\underbrace {\left( {3 \times 2} \right)}_{m{x_2}} - \underbrace {\left( {1 \times - 2} \right)}_{n{x_1}}}}{{3 - 1}} = \frac{{6 + 2}}{2} = 4\\&{y_D}\, = \frac{{\left( {3 \times - 1} \right) - \left( {1 \times 3} \right)}}{{3 - 1}} = \frac{{ - 6}}{2} = - 3\\&\Rightarrow \;\;\;\; \boxed{D = \left( {{x_D},\;{y_D}} \right) = \left( {4,\; - 3} \right)}\end{align}\]

These two points are plotted on \(AB\) (extended) in the figure below:

✍Note:

• \(AC\) is smaller than \(CB\), which is confirmed by the fact that \(AC:CB\) is less than 1.

• \(AD\) is larger than \(DB\), which is confirmed by the fact that \(AD:DB\) is greater than 1.

---

Example-2: Given two points \(A\) and \(B\), find the coordinates of the midpoint \(C\) of \(AB\), in terms of the coordinates of \(AB\).

Solution: Let \(A\) and \(B\) have the following coordinates:

\[A \equiv \left( {{x_1},\;{y_1}} \right),\;B \equiv \left( {{x_2},\;{y_2}} \right)\]

Consider the following figure:

Since \(C\) is the midpoint of \(AB\), it divides \(AB\) internally in the ratio 1:1. Using the section formula, the coordinates of \(C\) will be:

\[\begin{align}&\left\{ \begin{gathered}{x_C} = \frac{{\underbrace {1 \times {x_2}}_{m{x_2}} + \underbrace {1 \times {x_1}}_{n{x_1}}}}{{1 + 1}} = \frac{{{x_2} + {x_1}}}{2}\\{y_C}\, = \frac{{\underbrace {1 \times {y_2}}_{m{y_2}} + \underbrace {1 \times {y_1}}_{n{y_1}}}}{{1 + 1}} = \frac{{{y_2} + {y_1}}}{2}\end{gathered} \right.\\& \Rightarrow \;\;\;\; \boxed {C \equiv \left( {\frac{{{x_1} + {x_2}}}{2},\;\frac{{{y_1} + {y_2}}}{2}} \right)}\end{align}\]

✍Note: It is also known as Mid-point Formula.

This result makes sense, as the coordinates of \(C\) are the averages of the (respective) coordinates of \(A\) and \(B\), which is how things should be, since:

• the horizontal position of \(C\) is at the center of the horizontal positions of \(A\) and \(B\).

• the vertical position of \(C\) is at the center of the vertical positions of \(A\) and \(B\).

The following diagram shows this with more clarity:

---

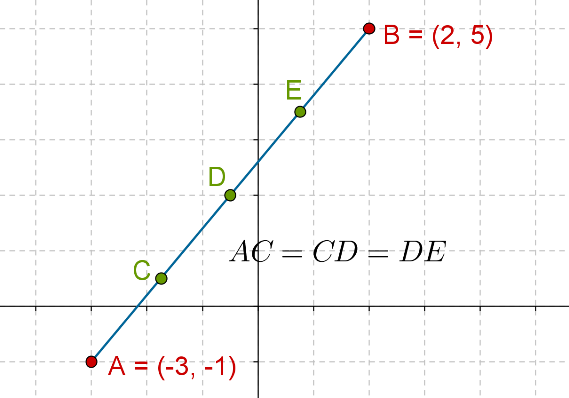
Challenge 1: Let \(A\) and \(B\) be two points with the following coordinates:

\[\begin{array}{l}A = \left( { - 3,\;1} \right)\\B = \left( {2,\;5} \right)\end{array}\]

The points \(C\), \(D\) and \(E\) divide \(AB\) into four equal parts, as shown in the figure below:

Determine the coordinates of \(C\), \(D\) and \(E\).

⚡Tip:

• \(C\) divides \(AB\) internally in the ratio 1:3 
• \(D\) divides \(AB\) internally in the ratio 2:2, that is, \(D\) is the midpoint of \(AB\), and,
• \(E\) divides \(AB\) internally in the ratio 3:1

---

✍Note: Before going to the next problem, we make an observation. Suppose that \(C\) divides \(AB\) internally in the ratio 1:3. Then, we can equivalently say that \(C\) divides \(AB\) internally in the ratio (1/3):1. Note that mathematically speaking, there is no difference between the two. Similarly, if someone tells you that \(D\) divides \(AB\) internally in the ratio (3/17):1, you could equivalently state that \(D\) divides \(AB\) internally in the ratio 3:17. This observation has an interesting consequence. Suppose that \(C\) divides \(AB\) in some unknown ratio. Rather than assuming that ratio to be (say) \(m:n\), we can assume it to be \(k:1\), as in the latter case, we have only one unknown variable, and our solution will be simplified. This becomes clear from the following example.

---

Example-3: In what ratio does the point \(C\left( { - 4,\;6} \right)\) divide the segment joining the points \(A\left( { - 6,\;10} \right)\) and \(B\left( {3,\; - 8} \right)\) ?

Solution: Suppose that the required ratio is k:1. We now use the section formula:

\[\begin{align}&{x_C} = \frac{{k{x_B} + {x_A}}}{{k + 1}},\;{y_C} = \frac{{k{y_B} + {y_A}}}{{k + 1}}\\&\Rightarrow \;\;\;\;\; - 4 = \frac{{3k - 6}}{{k + 1}},\;6 = \frac{{ - 8k + 10}}{{k + 1}}\\&\Rightarrow \;\;\;\;\; - 4k - 4 = 3k - 6,\;6k = - 8k + 10\\&\Rightarrow \;\;\;\;\; 7k = 2,\;14k = 4\\&\Rightarrow \;\;\;\;\; \boxed{k = \frac{2}{7},\;k = \frac{4}{{14}} = \frac{2}{7}}\end{align}\]

Note how we get consistent values of \(k\) from both relations. Thus, we conclude that \(C\) divides \(AB\) internally in the ratio \(\left( {2/7} \right):1\) , or equivalently, in the ratio \(2:7\) .

Alternative Method:

Let us suppose that instead of assuming the unknown ratio as \(k:1\), we had assumed it to be \(m:n\). In that case, our relations would have been as follows:

\[\begin{align}&{x_C} = \frac{{m{x_B} + n{x_A}}}{{m + n}},\;{y_C} = \frac{{m{y_B} + n{y_A}}}{{m + n}}\\& \Rightarrow  \;\;\;\;\; - 4 = \frac{{3m - 6n}}{{m + n}},\;6 = \frac{{ - 8m + 10n}}{{m + n}}\\&\Rightarrow  \;\;\;\;\;- 4m - 4n = 3m - 6n,\;6m + 6n =  - 8m + 10n\\&\Rightarrow \;\;\;\;\; 7m = 2n,\;14m = 4n\\&\Rightarrow  \;\;\;\;\; \frac{m}{n} = \frac{2}{7},\;\frac{m}{n} = \frac{4}{{14}} = \frac{2}{7}\end{align}\]

Once again, we get the same, consistent result, though we used two unknowns instead of one. This would not really matter in this particular example, but later on, when algebraic manipulations of coordinate expressions become difficult, it will generally be better to assume the unknown ratio in the form \(k:1\) rather than \(m:n\), even though mathematically there is no difference.

---

Challenge 2: In what ratio does the \(x\)-axis divide the segment joining the following points?

\[A = \left( { - 3,\;4} \right),\;B = \left( {2,\; - 5} \right)\]

⚡Tip: Let the segment \(AB\) intersect the \(x\)-axis at \(C\). Since \(C\) is a point on \(x\)-axis, let the coordinates of \(C\) be \(\left( {x,0} \right)\).

---

Example-4: Three vertices of a parallelogram \(ABCD\) are given below:

\[\begin{array}{l}A = \left( { - 2,\;2} \right)\\B = \left( { - 4,\; - 2} \right)\\C = \left( {3,\; - 1} \right)\end{array}\]

Find the coordinates of \(D\).

Solution: Let D be the point \(\left( {h,\;k} \right)\). Since the diagonals of the parallelogram must bisect each other, the midpoint of AC must be the same as the midpoint of BD. Thus, using the formula for the coordinates of the midpoint of a segment, we have:

\[\begin{align}&\left( {\frac{{{x_A} + {x_C}}}{2},\;\frac{{{y_A} + {y_C}}}{2}} \right) \equiv \left( {\frac{{{x_B} + {x_D}}}{2},\;\frac{{{y_B} + {y_D}}}{2}} \right)\\&\Rightarrow \;\;\;\;\; \left( {\frac{{ - 2 + 3}}{2},\;\frac{{2 + \left( { - 1} \right)}}{2}} \right) = \left( {\frac{{ - 4 + h}}{2},\; - \frac{{2 + k}}{2}} \right)\\&\Rightarrow  \;\;\;\;\;\left( {\frac{1}{2},\,\frac{1}{2}} \right) = \left( {\frac{{ - 4 + h}}{2},\;\frac{{ - 2 + k}}{2}} \right)\\&\Rightarrow  \;\;\;\;\; - 4 + h = 1,\; - 2 + k = 1\\&\Rightarrow \;\;\;\;\; h = 5,\;k = 3\end{align}\]

Thus,

\[\boxed{D = \left( {5,\;3} \right)}\]

Consider the following diagram to understand the solution better:

---

Example-5: A triangle has the vertices \(A\left( {{x_1},{y_1}} \right)\), \(B\left( {{x_2},{y_2}} \right)\), and \(C\left( {{x_3},{y_3}} \right)\) . Find the coordinates of the centroid \(G\) of the triangle.

Solution: The centroid is the point of intersection of the triangle’s medians:

The coordinates of the point \(D\) will be

\[D \equiv \left( {\frac{{{x_2} + {x_3}}}{2},\frac{{{y_2} + {y_3}}}{2}} \right)\]

Now, the centroid divides any median in the ratio 2:1. Thus, \({\rm{AG:GD =  2 : 1}}\). This means that we can now calculate the coordinates of \(G\) using the section formula, since the coordinates of \(A\) and \(D\) are both known. If the coordinates of \(G\) are \(\left( {{x_G},{y_G}} \right)\), then:

\[\begin{align}&{x_G} = \frac{{2 \times \left( {\frac{{{x_2} + {x_3}}}{2}} \right) + 1 \times {x_1}}}{{2 + 1}} = \frac{{{x_1} + {x_2} + {x_3}}}{3}\\&{y_G} = \frac{{2 \times \left( {\frac{{{y_2} + {y_3}}}{2}} \right) + 1 \times {y_1}}}{{2 + 1}} = \frac{{{y_1} + {y_2} + {y_3}}}{3}\end{align}\]

Thus, the coordinates of the centroid are

\[\boxed{G \equiv \left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3}} \right)}\]

---