Tangents From an External Point
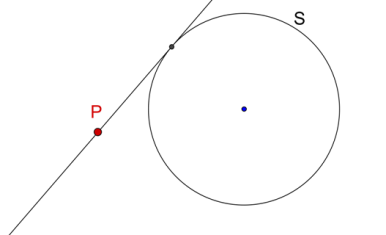
The following figure shows a circle S and a point P external to S. A tangent from P has been drawn to S. This is an example of a tangent from an external point:
How many tangents do you think can be drawn from an external point to a circle? The answer is two, and the following theorem proves this fact.
Theorem: Exactly two tangents can be drawn from an exterior point to a given circle.
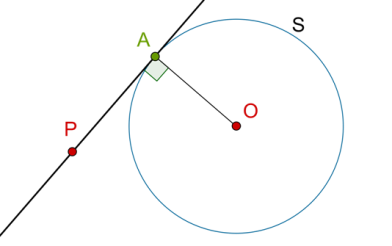
Consider the following figure, in which a tangent has been drawn from an exterior point P to a circle S (with center O), and the point of contact is A:
We will make use of the fact that \(\angle PAO\) must be 90 degrees.
Proof: Draw the circle S’ with PO as diameter. Clearly, A must lie on that circle, because we have seen that the angle in a semi-circle is a right angle:
We observe that S’ will intersect S in exactly two points, one of which is A, and the other we have labeled as B. The points of contact of the tangents from P to S must be the (two) points of intersection of S’ and S. Thus, exactly two tangents can be drawn from an exterior point to a circle: in this case, PA and PB. The other tangent (with the point of contact being B) has also been shown in the following figure:
We now prove some more properties related to tangents drawn from exterior points.
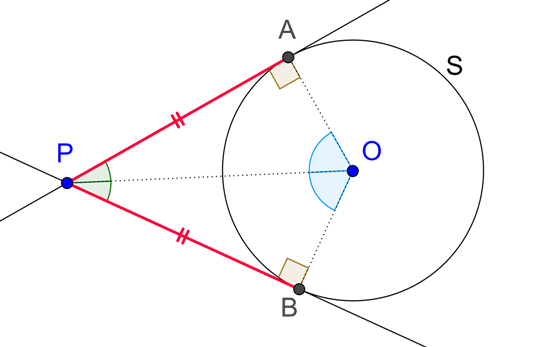
Theorem: Suppose that two tangents are drawn to a circle S from an exterior point P. Let the points of contact be A and B, as shown:
Our current theorem says that:
-
The lengths of these two tangents will be equal, that is, PA = PB.
-
They will subtend equal angles at the center, that is, \(\angle POA{\rm{ }} = \angle POB\).
-
The angle between them will be bisected by the line joining the exterior point and the center, that is, \(\angle APO{\rm{ }} = \angle BPO\) .
Proof: All the three parts will be proved if we show that \(\Delta PAO \) is congruent to \(\Delta PBO \). Comparing the two triangles, we see that:
-
OA = OB (radii of the same circle)
-
OP = OP (common)
-
\(\angle OAP{\rm{ }} = \angle OBP{\rm{ }} = {\rm{ }}{90^0}\)
Thus, by the RHS criterion, \(\Delta {\rm{PAO}}\) is congruent to \(\Delta {\rm{PBO}}\), and the truth of all the three assertions follows.
Example 1: Consider a circle S with center O. From an exterior point, exactly two tangents can be drawn to S. For a point on S, exactly one tangent can be drawn to S. How many tangents can be drawn to S from a point P inside S?
Solution: The answer, of course, is: none. Let us prove this rigorously. If PA is a tangent to S from an internal point P, then the points P, O and A will form a right-angled triangle with hypotenuse OP:
Note that OA is a radius of S, whereas since P is inside S, OP must be less than OA. Thus, the triangle above cannot exist. This proves that no tangent can be drawn from an interior point P to S.
You may be saying to yourself: this is so obvious! In fact, I can see it; why do I need to prove it?. The answer to this is that rigor is as important in Mathematics as intuition and visualization, as it leads to (apart from other things) a very good reasoning capability.
Example 2: Consider the following figure, where BC and BD are tangents to the circle:
What is the relation between \(\angle {\rm{DBC}}\) and \(\angle {\rm{DCA}}\) ?
Solution: Since BC is tangent to the circle at C, we note that \(\angle {\rm{BCA }} = {\rm{ }}{90^0}\) . Thus, \(\angle {\rm{BCD }} = \angle {\rm{BDC }} = {\rm{ }}{90^0}-\angle {\rm{DCA}}\). Applying the angle sum property in \(\Delta BCD\), we have:
\(\angle {\rm{DBC }} + \angle {\rm{BCD }} + \angle {\rm{BDC }} = {\rm{ }}{180^0}\)
è\(\angle {\rm{DBC }} + {\rm{ }}\left( {{{90}^0}-\angle {\rm{DCA}}} \right){\rm{ }} + {\rm{ }}\left( {{{90}^0}-\angle {\rm{DCA}}} \right){\rm{ }} = {\rm{ }}{180^0}\)
è \(\angle {\rm{DBC }}-{\rm{ }}2\angle {\rm{DCA }} = {\rm{ }}{0^0}\)
è \(\angle {\rm{DBC }} = {\rm{ }}2\angle {\rm{DCA}}\)
This is the required relation.
Example 3: From an external point B, tangents BC and BD are drawn to a circle with center A so that the length of each tangent is 4 cm, and AB = 5 cm. What is the radius of the circle?
Solution: Referring to the figure above for help (even though the length values in it are not the same as in the current problem), note that if AB is joined, then \(\Delta ABC\) will be right-angled at C, and so the Pythagoras Theorem applies:
\({\rm{A}}{{\rm{B}}^{\rm{2}}} = {\rm{ A}}{{\rm{C}}^{\rm{2}}} + {\rm{ B}}{{\rm{C}}^{\rm{2}}}\)
è \({\rm{A}}{{\rm{C}}^{\rm{2}}} = {\rm{ A}}{{\rm{B}}^{\rm{2}}}-{\rm{ B}}{{\rm{C}}^{\rm{2}}} = {\rm{ }}{{\rm{5}}^{\rm{2}}}-{\rm{ }}{4^2} = {\rm{ }}9\)
è \({\rm{AC }} = {\rm{ }}3{\rm{ }}cm\)
Example 4: Consider a chord AB of length 9 cm in a circle of radius 5 cm. Tangents at A and B intersect at C, as shown below:
What are the lengths of these tangents, that is, of CA and CB?
Solution: Join OC, and let it intersect AB at D:
Note that \(\angle {\rm{ADC }} = {\rm{ }}{90^0}\) . Now, compare \(\Delta {\rm{OAC}}\) with \(\Delta {\rm{ODA}}\) :
-
\(\angle {\rm{OAC }} = \angle {\rm{ODA }} = {\rm{ }}{90^0}\)
-
\(\angle {\rm{DOA }} = \angle {\rm{COA }}\left( {{\rm{common}}} \right)\)
Thus, the two triangles are similar by the AA similarity criterion. This means that OD:OA = AD:AC (make sure that you understand this). We know that OA = 5 cm, and AD is half of AB, which is 9 cm, so AD is 9/2 cm. We do not know the value of OD, but it can easily be calculated using the Pythagoras Theorem:
\({\rm{O}}{{\rm{D}}^{\rm{2}}} = {\rm{ O}}{{\rm{A}}^{\rm{2}}}-{\rm{ A}}{{\rm{D}}^{\rm{2}}} = {\rm{ }}{5^2}-{\rm{ }}{\left( {9/2} \right)^2} = {\rm{ }}19/4\)
è \({\rm{OD }} = {\rm{ }}\surd \left( {19/4} \right){\rm{ }} = {\rm{ }}\surd \left( {4.75} \right){\rm{ cm}}\)
We plug this value into the similarity relation OD:OA = AD:AC to get:
\[\begin{align}& {AC = \left( {OA \times AD} \right)/OD}\\& { = \left( {5 \times 9/2} \right)/\surd \left( {4.75} \right) \approx 10.3cm} \end{align}\]
This is the (approximate) length of the two tangents CA and CB.
Example 5: Consider two concentric circles of radii 3 cm and 5 cm. A chord AB of the larger circle touches the smaller circle at C. What is the length of AB?
Solution: Consider the following figure:
Note that since AB is the tangent to the smaller circle at C, OC must be perpendicular to AB. Thus, \(\Delta {\rm{OAC}}\) is right-angled at C. Also, C must be the midpoint of AB (why?), so \(AC = BC = \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/
\kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\rm{ }}AB\) Using the Pythagoras Theorem, we have:
\({\rm{A}}{{\rm{C}}^2} = {\rm{ O}}{{\rm{A}}^2}-{\rm{ O}}{{\rm{C}}^2} = {\rm{ }}{5^2}-{\rm{ }}{3^2} = {\rm{ }}16\)
è \({\rm{AC }} = {\rm{ }}4{\rm{ }}cm\)
è\({\rm{AB }} = {\rm{ }}2{\rm{ }} \times {\rm{ AC }} = {\rm{ }}8{\rm{ }}cm\)
Example 6: A quadrilateral EFGH circumscribes a circle as shown:
Show that EF + GH = EH + FG.
Solution: We use the fact that tangents from an external point to a circle are equal. So, EA = EB, FB = FC, GC = GD and HD = HA, as indicated:
Now, it is easy to observe that EF + GH has one part (of each color) from the four sides of the quadrilateral, and similarly, EH + FG has one part of each color from the four sides of the quadrilateral, and thus EF + GH = EH + FG. Make sure that you understand this reasoning; if you have any trouble, write down the values of the sums explicitly.
Example 7: Prove that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
Solution: Consider the following figure:
Focus your attention on \(\Delta {\rm{AOE}}\). Since \(\angle {\rm{OAE }} = {\rm{ }}{90^0}\), we note that \(\angle {\rm{AOE }} + \angle {\rm{AEO }} = {\rm{ }}{90^0}\). Also, \(\angle {\rm{AEO}}\) is half of \(\angle {\rm{E}}\) (can you see why?). Thus,
\[\angle AOE{\rm{ }} = {\rm{ }}{90^0}--{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \angle E\;\;\;\;\;\;\;\,...\left( 1 \right)\]
Similarly, we write the following relations:
\[\begin{align}& {\angle AOH{\rm{ }} = {\rm{ }}{{90}^0}-{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \angle H\;\;\;\;\;\;\;\,...\left( 2 \right)}\\& {\angle COF{\rm{ }} = {\rm{ }}{{90}^0}-{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \angle F\;\;\;\;\;\;\;\,...\left( 3 \right)}\\& {\angle COG{\rm{ }} = {\rm{ }}{{90}^0}-{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \angle G\;\;\;\;\;\;\;\,...\left( 4 \right)} \end{align}\]
If we add (1) and (2), we obtain:
\(\angle AOE{\rm{ }} + \angle AOH{\rm{ }} = {\rm{ }}{90^0}-{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \angle E{\rm{ }} + {\rm{ }}{90^0}-{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \angle H\)
è \(\angle EOH{\rm{ }} = {\rm{ }}{180^0}-{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} (\angle E{\rm{ }} + \angle H)\;\;\;\;\;\;\;\,...\left( 5 \right)\)
Similarly, adding (3) and (4) will yield:
\[\angle FOG{\rm{ }} = {\rm{ }}{180^0}-{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \left( {\angle F{\rm{ }} + \angle G} \right)\;\;\;\;\;\;\;\,...\left( 6 \right)\]
Finally, if we add (5) and (6) (remember that we are trying to show that \(\angle {\rm{EOH}}\) and \(\angle {\rm{FOG}}\) are supplementary), we will have:
\[\angle EOH{\rm{ }} + \angle FOG\]
\[ = {\rm{ }}{360^0}-{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \left( {\angle E{\rm{ }} + \angle F{\rm{ }} + \angle G{\rm{ }} + \angle H} \right)\]
But the sum of the four angles of the quadrilateral must be 3600, and so:
\[\angle EOH{\rm{ }} + \angle FOG{\rm{ }} = {\rm{ }}{360^0}-{\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \left( {{{360}^0}} \right){\rm{ }} = {\rm{ }}{180^0}\]
Thus, \(\angle {\rm{EOH}}\) and \(\angle {\rm{FOG}}\) are supplementary, and hence, \(\angle {\rm{EOF}}\) and \(\angle {\rm{GOH}}\) will also be supplementary.