Triangle Inequality in Vectors
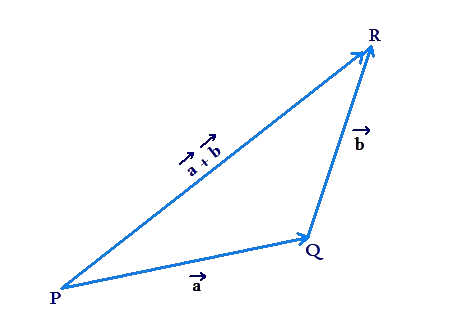
The following figure shows a triangle which is formed by the vectors \(\vec a\), \(\vec b\), and \(\vec a\, + \vec b\):
From plane geometry, we know that in any triangle, the sum of two sides is greater than the third side. In the figure above, PQ = \(\left| {\vec a} \right|\), QR = \(\left| {\vec b} \right|\) and PR = \(\left| {\vec a\, + \vec b} \right|\). Thus,
\[\left| {\vec a\, + \vec b} \right| < \left| {\vec a} \right| + \left| {\vec b} \right| ...\left( i \right)\]
Also, we know that the difference of two sides in a triangle is less than the third side. The difference of two quantities x and y can be written as \(\left| {x - y} \right|\). We take the modulus sign because we don’t know which quantity is larger: x or y; and when we say difference, we mean the positive difference. For example, the difference of 3 and 5 is \(\left| {3 - 5} \right| = 2\). Coming back to our triangle, the difference of PQ and QR can be written as |PQ \(- \) QR|. Thus,
\[\begin{array}{l}\left| {{\rm{PQ}} - {\rm{QR}}} \right| < \left| {{\rm{PR}}} \right|\\ \Rightarrow \,\,\,\left| {\left| {\vec a} \right| - \left| {\vec b} \right|} \right| < \left| {\vec a\, + \vec b} \right| & ...\left( {ii} \right)\end{array}\]
Combining (i) and (ii), we have the triangle inequality for vectors:
\[\underbrace {\left| {\left| {\vec a} \right| - \left| {\vec b} \right|} \right|}_{\scriptstyle{\rm{Difference\;of }}\atop\scriptstyle{\rm{two\;sides}}} < \underbrace {\left| {\vec a\, + \vec b} \right|}_{{\rm{Third\;side}}} < \underbrace {\left| {\vec a} \right| + \left| {\vec b} \right|}_{\scriptstyle{\rm{Sum\;of\; }}\atop\scriptstyle{\rm{two \;sides}}}\]
Don’t get intimidated by the seemingly complicated look of this inequality. It is simply an expression of the fact that any side in a triangle is less than the sum of the other two sides, and greater than their difference. In this case, the side \(\left| {\vec a\, + \vec b} \right|\) is less than the sum of the other two sides \(\left| {\vec a} \right| + \left| {\vec b} \right|\), and greater than their difference \(\left| {\left| {\vec a} \right| - \left| {\vec b} \right|} \right|\).
What if the vectors \(\vec a\) and \(\vec b\) are parallel (in the same direction), as shown in the figure below?
In this case, \(\left| {\vec a\, + \vec b} \right|\) will be equal to \(\left| {\vec a} \right| + \left| {\vec b} \right|\). Make sure you understand this.
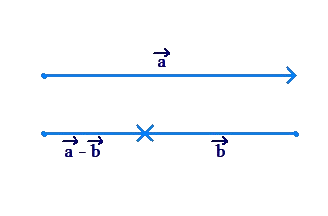
The other special case is when vectors \(\vec a\) and \(\vec b\) are anti-parallel (in the opposite directions), as shown below:
In this case, \(\left| {\vec a\, + \vec b} \right|\) is equal to the difference in the magnitudes of the two vectors, or \(\left| {\left| {\vec a} \right| - \left| {\vec b} \right|} \right|\).
If we incorporate these two special cases, we have the complete version of the triangle inequality:
\[\left| {\left| {\vec a} \right| - \left| {\vec b} \right|} \right| \le \left| {\vec a\, + \vec b} \right| \le \left| {\vec a} \right| + \left| {\vec b} \right|\]