Geometrical Interpretation Of Complex Equations

This section will give you more experience in dealing with complex numbers from a geometrical perspective. We will use the knowledge gained up to this point to interpret equations and inequations involving complex numbers geometrically. In particular, we will draw regions corresponding to equations and inequations on the complex plane; what this means will become quite clear in the following examples.

Example - 16

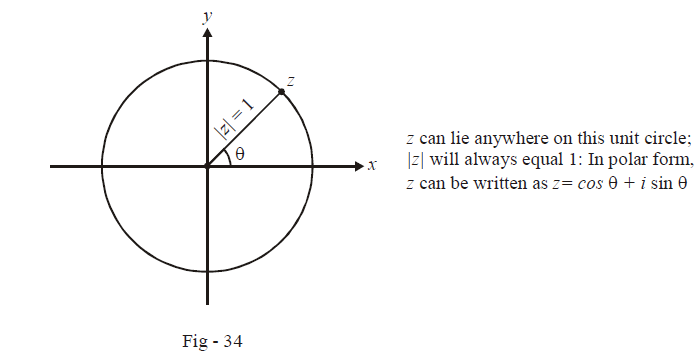
Interpret the equation \(\left| z \right| = 1\)  geometrically.

Solution: \(z\) is a (variable) complex number whose modulus is 1. This means that no matter what the direction in which \(z\) lies (i.e. no matter what its argument), the distance of \(z\) from the origin is always 1. Therefore, what path can \(z\) possibly trace out on the complex plane or in other words, what is the locus of \(z?\) Obviously, a circle of radius 1 centered at the origin.

Example - 17

Plot the regions that \(z\) represents if:

(a) \(\left| z \right| < 1\)      (b)    \(\left| z \right| > 2\)       (c)  \(1 < \left| z \right| < 2\)

Solution: (a) \(\left| z \right| < 1\)  means that the distance of \(z\) from the origin must be less than 1. Therefore, \(z\) must lie (anywhere) inside a circle of radius 1 centered at the origin.

(b) \(\left| z \right| > 2\)  means that the distance of \(z\) from the origin must be greater than 2. Therefore, \(z\) must lie (anywhere) outside a circle of radius 2 centered at the origin.

(c) \(1 < \left| z \right| < 2\) means geometrically that \(z\) must lie outside a circle of radius 1, but inside a circle of radius 2, both the circles being centered at the origin.

Example - 18

Plot the region represented by \(z\) if \(z\) satisfies

\[\begin{align}{}\left| {\arg (z)} \right| < \frac{\pi }{6}\\\left| z \right| < 3\end{align}\]

Solution: Since \(\begin{align}\left| {\arg (z)} \right| < \frac{\pi }{6}\end{align}\) this implies that\(\begin{align}\frac{{ - \pi }}{6} < \arg (z) < \frac{\pi }{6}\end{align}\)  . This means that \(z\) must lie in a triangular region with one edge making an angle \(\begin{align}\frac{\pi }{6}\end{align}\)  and the other edge making an angle \(\begin{align}\frac{{ - \pi }}{6}\end{align}\)  with the \(x\)-axis. Also, the distance of \(z\) from the origin must be less than 3. Thus, \(z\) lies in a region that is in the shape of a sector of a circle: