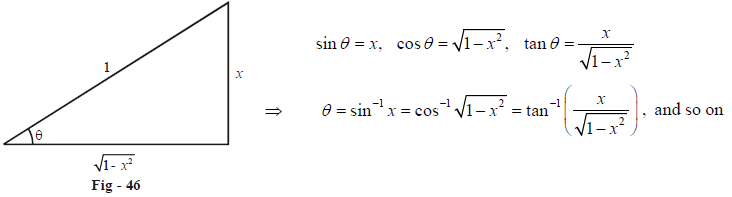Interconversion Between Inverse Trigonometric Ratios
The following sets of conversions should be fairly obvious:
(a) \(\begin{align}{\sin ^{ - 1}}x = {\cos ^{ - 1}}\sqrt {1 - {x^2}} = {\tan ^{ - 1}}\left( {\frac{x}{{\sqrt {1 - {x^2}} }}} \right) = {\cot ^{ - 1}}\left( {\frac{{\sqrt {1 - {x^2}} }}{x}} \right) = {\sec ^{ - 1}}\left( {\frac{1}{{\sqrt {1 - {x^2}} }}} \right) = {\text{cose}}{{\text{c}}^{ - 1}}\left( {\frac{1}{x}} \right)\end{align}\)
(b) \(\begin{align}{\cos ^{ - 1}}x = {\sin ^{ - 1}}\sqrt {1 - {x^2}} = {\tan ^{ - 1}}\left( {\frac{{\sqrt {1 - {x^2}} }}{x}} \right) = {\cot ^{ - 1}}\left( {\frac{x}{{\sqrt {1 - {x^2}} }}} \right) = {\sec ^{ - 1}}\frac{1}{x} = {\text{cose}}{{\text{c}}^{ - 1}}\left( {\frac{1}{{\sqrt {1 - {x^2}} }}} \right)\end{align}\)
(c) \(\begin{align}{\tan ^{ - 1}}x = {\sin ^{ - 1}}\left( {\frac{x}{{\sqrt {1 + {x^2}} }}} \right) = {\cos ^{ - 1}}\left( {\frac{1}{{\sqrt {1 + {x^2}} }}} \right) = {\cot ^{ - 1}}\left( {\frac{1}{x}} \right) = {\sec ^{ - 1}}\sqrt {1 + {x^2}} = {\text{cose}}{{\text{c}}^{ - 1}}\left( {\frac{{\sqrt {1 + {x^2}} }}{x}} \right)\end{align}\) etc.
This properties follow from definitions. For example:
We also have relations relating \(2{\tan ^{ - 1}}x\) to \({\sin ^{ - 1}}\) and \({\cos ^{ - 1}}\) :
Let \({\tan ^{ - 1}}x = \theta \quad \Rightarrow x = \tan \theta \) such that \(\begin{align}\theta \in \left( {\frac{{ - \pi }}{2},\;\frac{\pi }{2}} \right)\end{align}\)
Now,
\[\sin 2\theta = \frac{{2\tan \theta }}{{1 + {{\tan }^2}\theta }} = \frac{{2x}}{{1 + {x^2}}}\]
| If \(\begin{align}2\theta \in \left( {\frac{{ - \pi }}{2},\;\frac{\pi }{2}} \right)\end{align}\) | : | \(\begin{align}\Rightarrow \quad \theta \in \left( {\frac{{ - \pi }}{4},\;\frac{\pi }{4}} \right) \;\;\;\; &\Rightarrow \quad \;\;\;x = \tan \theta \in ( - 1,\;1)\, \\ &\Rightarrow\quad 2\theta = {\sin ^{ - 1}}\left( {\frac{{2x}}{{1 + {x^2}}}} \right) \\ \end{align} \) |
| If \(\begin{align}2\theta > \frac{\pi }{2}\end{align}\) | : | \(\begin{align}\Rightarrow \quad x > 1 \;\;\; \Rightarrow \quad \;\;2\theta = \pi - {\sin ^{ - 1}}\left( {\frac{{2x}}{{1 + {x^2}}}} \right)\end{align}\) |
| If \(\begin{align}2\theta < \frac{{ - \pi }}{2}\end{align}\) | : | \(\begin{align}\Rightarrow \; x < - 1 \;\;\;\;\;\quad \Rightarrow \quad\;\;\;\;\;2\theta = - \pi - {\sin ^{ - 1}}\left( {\frac{{2x}}{{1 + {x^2}}}} \right)\end{align}\) |
Thus,
\[2{\tan ^{ - 1}}x = \left\{ \begin{align} {\sin ^{ - 1}}\left( {\frac{{2x}}{{1 + {x^2}}}} \right), \quad x \in [ - 1,\;1] \\\\pi - {\sin ^{ - 1}}\left( {\frac{{2x}}{{1 + {x^2}}}} \right), x > 1 \\ - \pi - {\sin ^{ - 1}}\left( {\frac{{2x}}{{1 + {x^2}}}} \right), x < - 1 \\ \end{align} \right\}\]
Following a similar approach, show that
\[2{\tan ^{ - 1}}x = \left\{ \begin{align} {\cos ^{ - 1}}\left( {\frac{{1 - {x^2}}}{{1 + {x^2}}}} \right), x \in \left[ {0,\;\infty } \right) \\ - {\cos ^{ - 1}}\left( {\frac{{1 - {x^2}}}{{1 + {x^2}}}} \right), x \in \left( { - \infty ,\;0} \right] \\ \end{align} \right\}\]
- Live one on one classroom and doubt clearing
- Practice worksheets in and after class for conceptual clarity
- Personalized curriculum to keep up with school