Left Hand And Right Hand Limits

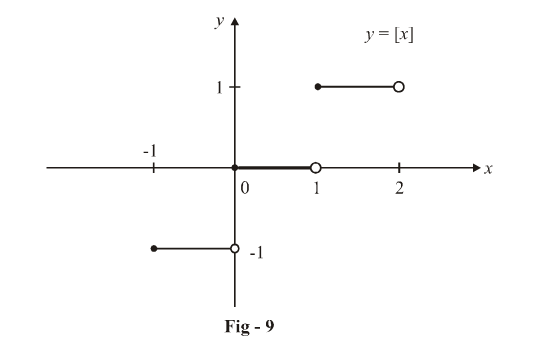
Lets consider another example now. We analyse the behaviour of \(f(x) = [x]\), as x approaches 0.

What happens when x approaches 0 from the right hand side? We see that [x] remains 0.

What happens when x approaches 0 from the left hand side? [x] has a value –1.

Note that we are not talking about what value [x] takes at x = 0. We are concerned with the behaviour of [x] in the neighbourhood of x = 0, that is, to the immediate left and right of x = 0.

Hence, we have:

\[\begin{align}&\mathop {\lim }\limits_{x \to {0^ + }} \left[ x \right] = 0\\&\mathop {\lim }\limits_{x \to {0^ - }} \left[ x \right] = - 1\\&\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {I^ + }} \left[ x \right] = I\\\mathop {\lim }\limits_{x \to {I^ - }} \left[ x \right] = I - 1\end{array} \right\}\;\;I\,\,{\rm{is}}\,{\rm{any}}\,{\rm{integer}}\end{align}\]

What about f (x) = {x}? This should be straightforward now:

\[\begin{align}&\mathop {\lim }\limits_{x \to {0^ + }} \left\{ x \right\} = 0\\\\&\mathop {\lim }\limits_{x \to {0^ - }} \left\{ x \right\} = 1\\\\ &\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {I^ + }} \left\{ x \right\} = 0\\\mathop {\lim }\limits_{x \to {I^ - }} \left\{ x \right\} = 1\end{array} \right\}\;\;I\;{\rm{is}}\,{\rm{any}}\,{\rm{integer}}\end{align}\]
 

We have now seen three different quantities regarding f(x)

Its possible that the value of the function at x = a is undefined, and yet the LHL or RHL (or both)exist.

For example, consider \(\begin{align}f\left( x \right) = \frac{{{x^2} - 1}}{{x - 1}}\end{align}\)

f (x) is clearly not defined at x = 1.

Every where else, f (x) can be written in a simple form as

\[f\left( x \right) = \frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{\left( {x - 1} \right)}} = x + 1\]

which is a straight line

This line has a hole at x = 1 because f (x) is undefined there. In the neighbourhood of

\[x = 1\left( {{\text{as}}\;x\, \to {1^ + }\;{\text{or}}\;\,x \to {1^ - }} \right),\]

f (x) ‘approaches’ the value 2 (though it never becomes 2, because to become 2, x has to have the value 1, which is not possible). We see that

\[{\text{LHL}} = \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = 2 = \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = {\text{RHL}}\]

To emphasize once again, in evaluating a limit at x = a, we are not concerned with what value f(x) assumes at precisely x = a; we are concerned with only how f(x) behaves as x approaches or nearly becomes a, whether from the left hand or right hand side, giving rise to LHL and RHL respectively.

And finally, the limit of f(x) at x = a is said to exist if the function approaches the same value from both sides

Note: We have used the concept of \(\infty \) (infinity) in the discussions above. Lets discuss this concept in some what more detail:

\( \Rightarrow \) Infinity does not stand for any particular real number. In fact, it cannot be defined precisely.This is a deep concept. For any number you can think of, no matter how large, infinity is still larger. When we say that \(x \to \infty ,\) we mean that x increase in an unbounded fashion, that is, becomes indefinitely large.

\( \Rightarrow \) We cannot apply the normal rules of arithmetic to infinity. For example, saying that

\[\infty - \infty = 0\;\;{\rm{or}}\;\;\frac{\infty }{\infty } = 1\]

is absurd because such quantities are not defined.

\( \Rightarrow \) It should be clear now that an expression like \(x \to \infty \) defines a tendency (of unbounded increase)

Consider a fraction \(\begin{align}f = \frac{{{\rm{Num}}}}{{{\rm{Den}}}}\end{align}\)

As x \( \to \) a, if (Num) (a finite number) and (Den) \( \to \infty \) , then f tends to become infinitesimally small or \(f \to 0\) .

Such cases are listed out below. Observe the details carefully

\(\begin{align}
&\qquad  \qquad  \qquad  \qquad  \qquad f\;{\rm{ = }}\;\frac{{{\rm{Num}}}}{{{\rm{Den}}}}\\
\rm\bf{(i)}\qquad&\left. \begin{array}{l}
 \mathop {{\rm{lim}}}\limits_{x \to {\rm{a}}} \left( {{\rm{Num}}} \right) = {\rm{finite}}\\
\mathop {{\rm{lim}}}\limits_{x \to {\rm{a}}} \left( {{\rm{Den}}} \right)\;\; = {\rm{infinity}}
\end{array} \right\}\;\;\Rightarrow \;\;\mathop {{\rm{lim}}}\limits_{{\rm{x}} \to {\rm{a}}} f = 0\\
\\
\rm\bf{(ii)}\qquad&\left. \begin{array}{l}
\mathop {{\rm{lim}}}\limits_{x \to a} \left( {{\rm{Num}}} \right) = {\rm{infinity}}\\
\mathop {{\rm{lim}}}\limits_{x \to a} \left( {{\rm{Den}}} \right)\;\; = {\rm{finite}}
\end{array} \right\} \Rightarrow \;\;\mathop {{\rm{lim}}}\limits_{x \to a} f = \infty \\
\\
\rm\bf{(iii)}\qquad&\left. \begin{array}{l}
\mathop {{\rm{lim}}}\limits_{x \to a} \left( {{\rm{Num}}} \right) = 0\\
\mathop {{\rm{lim}}}\limits_{x \to a} \left( {{\rm{Den}}} \right)\;\; = {\rm{non - zero}}
\end{array} \right\}\;\; \Rightarrow \;\;\mathop {{\rm{lim}}}\limits_{x \to a} f = 0\\
\\
\rm\bf{(iv)}\qquad&\left. \begin{array}{l}
\mathop {{\rm{lim}}}\limits_{x \to a} \left( {{\rm{Num}}} \right) = p\\
\mathop {{\rm{lim}}}\limits_{x \to a} \left( {{\rm{Den}}} \right) = q \ne 0
\end{array} \right\}\;\;\Rightarrow \;\;\mathop {{\rm{lim}}}\limits_{x \to a} f = \frac{p}{q}
\end{align}\)

\( \Rightarrow \,\,\,\,\,\,{\rm{Suppose}}\,{\rm{that}}\,\mathop {\lim }\limits_{x \to a} \left( {{\rm{Num}}} \right) = 0\,\,\,{\rm{and}}\,\,\,\mathop {\lim }\limits_{x \to a} \left( {{\rm{Den}}} \right) = 0\)\({\rm{or}}\;\;\;\,\mathop {\lim }\limits_{x \to a} \left( {{\rm{Num}}} \right) = \infty \,\,\,{\rm{and}}\,\,\,\mathop {\lim }\limits_{x \to a} \left( {{\rm{Den}}} \right) = \infty ,\)

Then f is of the form:

\[f = \frac{{ \to 0}}{{ \to 0}}\,\,\,{\text{or}}\,\,\,\frac{{ \to \infty }}{{ \to \infty }}\]

The tendency (or limits) of such forms may or may not exist

For example, if \(\left( \rm{Num} \right) = {\rm{ }}{x^2}-{\rm{ }}1\;{\rm{and }}\left( {Den} \right){\rm{ }} = {\rm{ }}x{\rm{ }}-{\rm{ }}1,\)

then \(\mathop {\lim }\limits_{x \to 1} \left( {{\rm{Num}}} \right) = 0 \,{\rm{and}}\;\;\;\mathop {\lim }\limits_{x \to 1} \left( {{\rm{Den}}} \right) = 0,\,\;{\rm{so}}\)

that f is of the form \(\frac{0}{0}\) . But as we have seen earlier, the limit of f exists, as \(x \to 1\)

\[\mathop {\lim }\limits_{x \to 1} f = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = 2\]

Limits of the form \(\frac{0}{0},\frac{\infty }{\infty },\infty - \infty ,\,\,\,\infty \times 0,\,\,\,{1^\infty },\) 0º are called indeterminate forms. The limits of such forms may exist but it cannot be determined by simple observation (hence the name indeterminate). Such forms need to be reduced into determinate forms for which the limit can be determined. In the above case, for example, an indeterminate form \(\begin{align}\left( {\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}}} \right)\end{align}\) was reduced into a determinate form \(\left( {\mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right)} \right)\) , whose limit can be determined by substitution of x = 1

TRY YOURSELF - I

Q1.  What should be the limit of the following sequence?

\[\left\{ {\;1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\;...\;} \right\}\]

Q2. What should be the limit of these sequences?

(a) \(1,\; - 1,\;1,\; - 1,\;1,\; - 1,\;....\)

(b) \(\begin{align}1, - \frac{1}{2},\frac{1}{4}, - \frac{1}{8},\frac{1}{{16}}\;,\;...\end{align}\)

(c) \(1,2,4,8,16,\;...\)

Q3. Find the following limits:

(a) \(\mathop {\lim }\limits_{x \to 0} \left( {1 + x + {x^2}} \right)\)

(b) \(\mathop {\lim }\limits_{x \to \sqrt 2 } \left( {{x^4} + {x^2} + 1} \right)\)

(c) \(\begin{align}\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 3x + 2}}{{x - 2}}\end{align}\)

(d) \(\mathop {\lim }\limits_{x \to \; - \infty } {2^x}\)