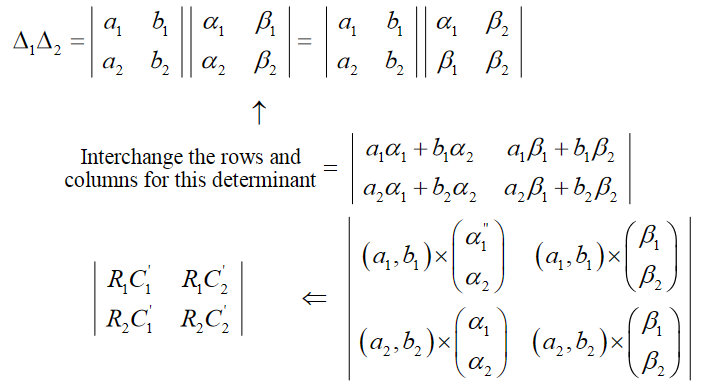Multiplication Of Determinants

Property - 7 :  Multiplication of determinants

Suppose we have two 2 × 2 determinants

\[{{\Delta }_{1}}=\left| \ \begin{matrix}   {{a}_{1}} & {{b}_{1}}  \\   {{a}_{2}} & {{b}_{2}}  \\\end{matrix}\  \right| \qquad \qquad{{\Delta }_{2}}=\left| \ \begin{matrix}   {{\alpha }_{1}} & {{\beta }_{1}}  \\   {{\alpha }_{2}} & {{\beta }_{2}}  \\\end{matrix}\  \right|\]

and we wish to find \({{\Delta }_{1}}{{\Delta }_{2}}.\) By expansion,

\[{{\Delta }_{1}}={{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}},\ \ {{\Delta }_{2}}={{\alpha }_{1}}{{\beta }_{2}}-{{\alpha }_{2}}{{\beta }_{1}}\]

so

\[{{\Delta }_{1}}{{\Delta }_{2}}=\left( {{a}_{1}}{{\alpha }_{1}}{{b}_{2}}{{\beta }_{2}}+{{a}_{2}}{{\alpha }_{2}}{{b}_{1}}{{\beta }_{1}} \right)-\left( {{a}_{1}}{{\alpha }_{1}}{{b}_{2}}{{\beta }_{1}}+{{a}_{2}}{{\alpha }_{1}}{{b}_{1}}{{\beta }_{2}} \right) \qquad \qquad \dots (1) \]

To find a more enlightening expression, we introduce the term \(\left( {{a}_{1}}{{a}_{2}}{{\alpha }_{1}}{{\alpha }_{2}}+{{b}_{1}}{{b}_{2}}{{\beta }_{1}}{{\beta }_{2}} \right):\)  add and subtract this. Adding this to the first bracket in (1) will generate the factors \(\left( {{a}_{1}}{{\alpha }_{1}}+{{b}_{1}}{{\beta }_{1}} \right)\left( {{a}_{2}}{{\alpha }_{2}}+{{b}_{2}}{{\beta }_{2}} \right).\) Make sure you verify this. Similarly, when we subtract the same term from (1), it will combine with the second bracket to generate the factors \(\left( {{a}_{1}}{{\alpha }_{2}}+{{b}_{1}}{{\beta }_{2}} \right)\left( {{a}_{2}}{{\alpha }_{1}}+{{b}_{2}}{{\beta }_{1}} \right).\) Therefore, (1) can be rearranged as

\[\begin{align}   {{\Delta }_{1}}{{\Delta }_{2}}&=\left( {{a}_{1}}{{\alpha }_{1}}+{{b}_{1}}{{\beta }_{1}} \right)\left( {{a}_{2}}{{\alpha }_{2}}+{{b}_{2}}{{\beta }_{2}} \right)-\left( {{a}_{1}}{{\alpha }_{2}}+{{b}_{1}}{{\beta }_{2}} \right)\left( {{a}_{2}}{{\alpha }_{1}}+{{b}_{2}}{{\beta }_{1}} \right) \\ \\  & =\left| \ \begin{matrix}   {{a}_{1}}{{\alpha }_{1}}+{{b}_{1}}{{\beta }_{1}} & {{a}_{1}}{{\alpha }_{2}}+{{b}_{1}}{{\beta }_{2}}  \\   {{a}_{2}}{{\alpha }_{1}}+{{b}_{2}}{{\beta }_{1}} & {{a}_{2}}{{\alpha }_{2}}+{{b}_{2}}{{\beta }_{2}}  \\\end{matrix}\  \right| \\ \end{align}\]

Look carefully at the term in \({{\Delta }_{1}}{{\Delta }_{2}}\) at the (1, 1) position. It is a ‘sort of’ product of the row (a₁, b₁) from \({{\Delta }_{1}}\ \text{and}\ \left( {{\alpha }_{1}},{{\beta }_{1}} \right)\ \text{from}\ {{\Delta }_{2}}:\)

\[{{a}_{1}}{{\alpha }_{1}}+{{b}_{1}}{{\beta }_{1}}=\left( {{a}_{1}},{{b}_{1}} \right)\times \left( {{\alpha }_{1}},{{\beta }_{1}} \right)\]

Similarly, at (1, 2) :

\[{{a}_{1}}{{\alpha }_{2}}+{{b}_{1}}{{\beta }_{2}}=\left( {{a}_{1}},{{b}_{1}} \right)\times \left( {{\alpha }_{2}},{{\beta }_{2}} \right)\]

At (2, 1) :

\[{{a}_{2}}{{\alpha }_{1}}+{{b}_{2}}{{\beta }_{1}}=\left( {{a}_{2}},{{b}_{2}} \right)\times \left( {{\alpha }_{1}},{{\beta }_{1}} \right)\]

And at (2, 2) :

\[{{a}_{2}}{{\alpha }_{2}}+{{b}_{2}}{{\beta }_{2}}=\left( {{a}_{2}},{{b}_{2}} \right)\times \left( {{\alpha }_{2}},{{\beta }_{2}} \right)\]

If the two rows of \({{\Delta }_{1}}\) are denoted as \({{R}_{1}},{{R}_{2}}\) and the two rows of \({{\Delta }_{2}}\ \text{as}\ R_{1}^{'},R_{2}^{'}\), then,

\[{{\Delta }_{1}}{{\Delta }_{2}}=\left| \begin{gathered}  & \ {{R}_{1}} \\  & \ {{R}_{2}}\  \\ \end{gathered} \right|\times \left| \begin{gathered}  & \ R_{1}^{'} \\  & \ R_{2}^{'}\  \\ \end{gathered} \right|\ \ =\ \ \left| \begin{matrix}   {{R}_{1}}R_{1}^{'} & {{R}_{1}}R_{2}^{'}  \\   \ {{R}_{2}}R_{1}^{'} & {{R}_{2}}R_{2}^{'}  \\\end{matrix}\  \right|\ \]

Since a determinant stays the same by interchaning the rows and columns, it should be obvious that similar to ‘row-by-row’ multiplication that we’ve encountered above, we can also have ‘row-by-column’ multiplication and ‘column-by-column’ multiplication. For example,

This is a row-by-column multiplication. Similarly, we’ll have column-by-column multiplication.

What if we have to multiply two 3 × 3 determinants?

\[{{\Delta }_{1}}=\left| \ \begin{matrix}   {{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\   {{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\   {{a}_{3}} & {{b}_{3}} & {{c}_{3}}  \\\end{matrix}\  \right|\ \ {{\Delta }_{2}}=\ \left| \ \begin{matrix}   {{\alpha }_{1}} & {{\beta }_{1}} & {{\gamma }_{1}}  \\   {{\alpha }_{2}} & {{\beta }_{2}} & {{\gamma }_{2}}  \\   {{\alpha }_{3}} & {{\beta }_{3}} & {{\gamma }_{3}}  \\\end{matrix}\  \right|\]

In terms of rows,

\[{{\Delta }_{1}}=\left| \ \begin{matrix}   {{R}_{1}}  \\   {{R}_{2}}  \\   {{R}_{3}}  \\\end{matrix}\  \right|\ \ {{\Delta }_{2}}=\ \left| \ \begin{matrix}   R_{1}^{'}  \\   R_{2}^{'}  \\   R_{3}^{'}  \\\end{matrix}\  \right|\]

The multiplication process is analogous to the 2 × 2 case:

\[{{\Delta }_{1}}{{\Delta }_{2}}=\left| \ \begin{matrix}   {{R}_{1}}R_{1}^{'} & {{R}_{1}}R_{2}^{'} & {{R}_{1}}R_{3}^{'}  \\   {{R}_{2}}R_{1}^{'} & {{R}_{2}}R_{2}^{'} & {{R}_{2}}R_{3}^{'}  \\   {{R}_{3}}R_{1}^{'} & {{R}_{3}}R_{2}^{'} & {{R}_{3}}R_{3}^{'}  \\\end{matrix}\  \right|\ \]

Rows are multiplied similarly as before. For example,

\[{{R}_{1}}R_{2}^{'}=\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)\ \times \ \left( {{\alpha }_{2}},{{\beta }_{2}},{{\gamma }_{2}} \right)=\left( {{a}_{1}}{{\alpha }_{2}}+{{b}_{1}}{{\beta }_{2}}+{{c}_{1}}{{\gamma }_{2}} \right)\]

As in the 2 × 2 case, we can have row-by-column and column-by-column multiplication.

To gain a little practice, let us evaluate the numerical product of two 3 × 3 determinants:

\[{{\Delta }_{1}}=\left| \begin{matrix}   1 & 3 & \ 2  \\   4 & 2 & -1  \\   5 & -1 & 3  \\ \end{matrix} \right| \qquad {{\Delta }_{2}}=\left| \begin{matrix}   2 & -1 & \ 3  \\   3 & 1 & 4  \\   0 & 5 & 2  \\\end{matrix} \right|\]

Note that  \({{\Delta }_{1}}=-74\ \text{and}\ {{\Delta }_{2}}=15,\ \ \text{so}\ {{\Delta }_{1}}{{\Delta }_{2}}\) should be –1110.

Now, let us evaluated \({{\Delta }_{1}}{{\Delta }_{2}}\) through row-by-row multiplication:

We have,

\(\begin{align}   {{R}_{1}}R_{1}^{'}&=\left( 1\ \ 3\ \ 2 \right)\left( 2\ \ -1\ \ 3 \right) \\  & =5 \\ \end{align}\)	\(\begin{align}   {{R}_{1}}R_{2}^{'}&=\left( 1\ \ 3\ \ 2 \right)\left( 3\ \ 1\ \ 4 \right) \\  & =14 \\ \end{align}\)	\(\begin{align}   {{R}_{1}}R_{3}^{'}&=\left( 1\ \ 3\ \ 2 \right)\left( 0\ \ 5\ \ 2 \right) \\  & =19 \\ \end{align}\)
\(\begin{align}   {{R}_{2}}R_{1}^{'}&=\left( 4\ \ 2\ \ -1 \right)\left( 2\ \ -1\ \ 3 \right) \\  & =3 \\ \end{align}\)	\(\begin{align}   {{R}_{2}}R_{2}^{'}&=\left( 4\ \ 2\ \ -1 \right)\left( 3\ \ 1\ \ 4 \right) \\  & =10 \\ \end{align}\)	\(\begin{align}   {{R}_{2}}R_{3}^{'}&=\left( 4\ \ 2\ \ -1 \right)\left( 0\ \ 5\ \ 2 \right) \\  & =8 \\ \end{align}\)
\(\begin{align}  {{R}_{3}}R_{1}^{'} &=\left( 5\ \ -1\ \ 3 \right)\left( 2\ \ -1\ \ 3 \right) \\  & =20 \\ \end{align}\)	\(\begin{align}  {{R}_{3}}R_{2}^{'} &=\left( 5\ \ -1\ \ 3 \right)\left( 3\ \ 1\ \ 4 \right) \\  & =26 \\ \end{align}\)	\(\begin{align}   \ {{R}_{3}}R_{3}^{'}&=\left( 5\ \ -1\ \ 3 \right)\left( 0\ \ 5\ \ 2 \right) \\  & =1 \\ \end{align}\)

So,

\[\begin{align}   {{\Delta }_{1}}{{\Delta }_{2}}&=\left| \ \begin{matrix}   5 & 14 & 19  \\   3 & 10 & 8  \\   20 & 26 & 1  \\\end{matrix}\  \right|=-990+2198-2318 \\\\  & =-1110 \\ \end{align}\]

As an exercise, evaluate the same product through row-by-column and column-by-column multiplication.

Example - 14

Evaluate

\[\Delta =\left| \ \begin{matrix}   {{\left( {{a}_{1}}-{{b}_{1}} \right)}^{2}} & {{\left( {{a}_{1}}-{{b}_{2}} \right)}^{2}} & {{\left( {{a}_{1}}-{{b}_{3}} \right)}^{2}}  \\   {{\left( {{a}_{2}}-{{b}_{1}} \right)}^{2}} & {{\left( {{a}_{2}}-{{b}_{2}} \right)}^{2}} & {{\left( {{a}_{2}}-{{b}_{3}} \right)}^{2}}  \\   {{\left( {{a}_{3}}-{{b}_{1}} \right)}^{2}} & {{\left( {{a}_{3}}-{{b}_{2}} \right)}^{2}} & {{\left( {{a}_{3}}-{{b}_{3}} \right)}^{2}}  \\\end{matrix}\  \right|\]

Solution: The trick is in recognizing the fact that \(\Delta \) can be expressed as a product of two 3 × 3 determinants \({{\Delta }_{1}}\ \text{and}\ {{\Delta }_{2}}\) . To arrive at this product, we note how elements of row 1 can be expressed as products of rows.

\[\begin{align}  & {{\left( {{a}_{1}}-{{b}_{1}} \right)}^{2}}=a_{1}^{2}-2{{a}_{1}}{{b}_{1}}+b_{1}^{2}=\left( a_{1}^{2}\ \ \ 2{{a}_{1}}\ \ \ 1 \right)\ \times \ \left( 1\ \ -{{b}_{1}}\ \ \ b_{1}^{2} \right) \\  &  \\  & {{\left( {{a}_{1}}-{{b}_{2}} \right)}^{2}}=a_{1}^{2}-2{{a}_{1}}{{b}_{2}}+b_{2}^{2}=\left( a_{1}^{2}\ \ \ 2{{a}_{1}}\ \ \ 1 \right)\ \times \ \left( 1\ \ -{{b}_{2}}\ \ \ b_{2}^{2} \right) \\  &  \\  & {{\left( {{a}_{1}}-{{b}_{3}} \right)}^{2}}=a_{1}^{2}-2{{a}_{1}}{{b}_{3}}+b_{3}^{2}=\left( a_{1}^{2}\ \ \ 2{{a}_{1}}\ \ \ 1 \right)\ \times \ \left( 1\ \ -{{b}_{3}}\ \ \ b_{3}^{2} \right) \\ \end{align}\]

This means that we now know how to fill \({{R}_{1}}\) of  \({{\Delta }_{1}}\) and the three rows of \({{\Delta }_{2}}\)

\[\Delta =\left| \ \begin{matrix}   a_{1}^{2} & 2{{a}_{1}} & 1  \\   \leftarrow  & ? & \to   \\   \leftarrow  & ? & \to   \\\end{matrix}\  \right|\ \ \times \ \ \left| \ \begin{matrix}   1 & -{{b}_{1}} & b_{1}^{2}  \\   1 & -{{b}_{2}} & b_{2}^{2}  \\   1 & -{{b}_{3}} & b_{3}^{2}  \\\end{matrix}\  \right|\]

But now, the other rows of \({{\Delta }_{1}}\) should be evident immediately by symmetry:

\[\Delta =\left| \ \begin{matrix}   a_{1}^{2} & 2{{a}_{1}} & 1  \\   a_{2}^{2} & 2{{a}_{2}} & 1  \\   a_{3}^{2} & 2{{a}_{3}} & 1  \\\end{matrix}\  \right|\ \ \times \ \,\,\left| \ \begin{matrix}   1 & -{{b}_{1}} & b_{1}^{2}  \\   1 & -{{b}_{2}} & b_{2}^{2}  \\   1 & -{{b}_{3}} & b_{3}^{2}  \\\end{matrix}\  \right|\ \ \]

These two determinants are separately very easy to evaluate; we have already done that in Example - 4:

\[\Delta =2\left( {{a}_{1}}-{{a}_{2}} \right)\left( {{a}_{2}}-{{a}_{3}} \right)\left( {{a}_{3}}-{{a}_{1}} \right)\left( {{b}_{1}}-{{b}_{2}} \right)\left( {{b}_{2}}-{{b}_{3}} \right)\left( {{b}_{3}}-{{b}_{1}} \right)\]

Example - 15

Evaluate  \(\Delta =\left| \ \begin{matrix}   \cos \left( a-p \right) & \cos \left( a-q \right) & \cos \left( a-r \right)  \\   \cos \left( b-p \right) & \cos \left( b-q \right) & \cos \left( b-r \right)  \\   \cos \left( c-p \right) & \cos \left( c-q \right) & \cos \left( c-r \right)  \\\end{matrix}\  \right|\)

Solution: Once again, the determinant can be split into a product. For example,

\[\begin{align} &\cos \left( a-p \right)=\cos a\cos p+\sin a\sin p \\  & =\left( \cos a\ \ \ \sin a\ \ \ \ 0 \right)\left( \cos p\ \ \ \sin p\ \ \ \ 0 \right) \\ \end{align}\]

Thus,

\[\begin{align}   \Delta &=\left| \ \begin{matrix}   \cos a & \sin a & 0  \\   \cos b & \sin b & 0  \\   \cos c & \sin c & 0  \\\end{matrix}\  \right|\ \ \times \ \ \left| \ \begin{matrix}   \cos p & \sin p & 0  \\   \cos q & \sin q & 0  \\   \cos r & \sin r & 0  \\\end{matrix}\  \right| \\\\  & =0 \\ \end{align}\]

TRY YOURSELF - II

Q.1      Evaluate

\[\Delta =\left| \ \begin{matrix}   1 & {{a}^{2}} & {{a}^{3}}  \\   1 & {{b}^{2}} & {{b}^{3}}  \\   1 & {{c}^{2}} & {{c}^{3}}  \\\end{matrix}\  \right|\]

Q.2      Evaluate

\[\Delta =\left| \ \begin{matrix}   a & b & c  \\   {{a}^{2}} & {{b}^{2}} & {{c}^{2}}  \\   bc & ca & ab  \\\end{matrix}\  \right|\]

Q.3      If a, b, c are unequal, and if

\[\left| \ \begin{matrix}   a & {{a}^{2}} & 1+{{a}^{3}}  \\   b & {{b}^{2}} & 1+{{b}^{3}}  \\   c & {{c}^{2}} & 1+{{c}^{3}}  \\\end{matrix}\  \right|=0\]

Find the value of abc.

Q.4      Without expanding at any stage, show that

\[\left| \ \begin{matrix}   a+b & b+c & c+a  \\   b+c & c+a & a+b  \\   c+a & a+b & b+c  \\\end{matrix}\  \right|=2\ \left| \ \begin{matrix}   a & b & c  \\   b & c & a  \\   c & a & b  \\\end{matrix}\  \right|\]

Q.5      Evaluate

\[\Delta =\left| \ \begin{matrix}   a-b-c & 2a & 2a  \\   2b & b-c-a & 2b  \\   2c & 2c & c-a-b  \\\end{matrix}\  \right|\]