Lets consider a third form to represent a line. From the figure below, observe carefully that to uniquely determine a line, we could also specify the length of the perpendicular dropped from the origin to that line and the orientation (inclination) of that perpendicular:

To determine the equation of this line, assume any point P on the line with the co-ordinate (x, y). Observe the geometry described in the figure below carefully:
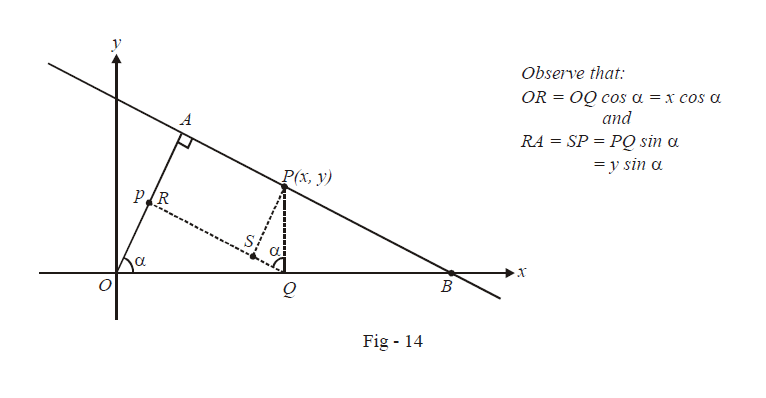
From the figure, note that
\[\begin{align} &\qquad \quad\; OR + RA = OA = p \\ &
\Rightarrow \qquad \boxed{x\cos \alpha + y\sin \alpha = p}\,\,\,\,\,\,\,\,\,\,\,\,\,:{\;\mathbf{Normal}}{\text{ }}{\mathbf{form}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \nearrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \quad\quad\nwarrow \\ &\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{inclination}\,\,\text{of}\,\,\,\,\,\,\,\,\text{length}\,\text{of} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{perpendicular}\,\,\,\,\,\,\,\text{perpendicular} \end{align} \]

