Arctan 1 (Tan Inverse 1)
Before we evaluate the value of arctan 1, let us recall the meaning of arctan. Arctan is the abbreviated form of arctangent which is one of the main six inverse trigonometric functions (inverse of the tangent function), also known as the tan inverse. The value of arctan 1 or tan inverse 1 is equal to π/4 radians or 45 degrees. Tan inverse 1 gives the measure of an angle of a right-angled triangle when the ratio of the perpendicular and the base is equal to 1. We can evaluate this value using the fact that the value of the tangent function at 45 degrees angle is equal to 1.
In this article, we will understand the evaluation of the value of arctan 1 in degrees and radians using trigonometric facts and formulas. We will also solve a few examples and evaluate the value of various inverse trigonometric functions using the value of arctan 1 to understand the concept better.
| 1. | What is Arctan 1? |
| 2. | Finding the Tan Inverse 1 Value |
| 3. | Arctan 1 in Degrees |
| 4. | Arctan 1 in Radians |
| 5. | Value of Tan Inverse 1 in Terms of Pi |
| 6. | FAQs on Arctan 1 |
What is Arctan 1?
Arctan 1 (or tan inverse 1) gives the value of the inverse trigonometric function arctan when the ratio of the perpendicular and the base of a right-angled triangle is equal to 1. In other words, we can say that the tan inverse 1 value is the measure of the angle of a right-angled triangle when the ratio of the opposite side and the adjacent side to the angle is equal to 1. The value of tan inverse 1 is equal to 45° or π/4 radians. Let us prove this value of arctan 1 in the next section.

Finding the Tan Inverse 1 Value
As discussed in the previous section, tan inverse 1 gives the measure of the angle of a right-angled triangle when the ratio of the opposite side and the adjacent side of the angle is equal to 1. Since the ratio is equal to 1, this implies we can write it as
Opposite Side / Adjacent Side = 1
⇒ Opposite Side = Adjacent Side
This implies that the right-angled triangle is isosceles. We know that the sum of all angles in a triangle is equal to 180° and in an isosceles triangle, angles opposite to equal sides are equal. So, consider an isosceles right-angled triangle ABC right angled at B where the lengths of the perpendicular AB and base BC are the same. Then, we have
∠A + ∠B + ∠C = 180° --- [Using angle sum property of a triangle]
⇒ ∠A + 90° + ∠C = 180° --- [Because angle B is a right angle]
⇒ ∠A + 90° + ∠A = 180° --- [Since AB = BC, this implies angle A is equal to angle C because angles opposite to equal sides are equal.]
⇒ 2∠A + 90° = 180°
⇒ 2∠A = 180° - 90°
⇒ ∠A = 90°/2
⇒ ∠A = 45°
Therefore, angle A = angle C = 45°
As discussed above, arctan 1 gives the measure of the angle of a right-angled triangle when the ratio of the opposite side and the adjacent side of the angle is equal to 1, hence we have determined the measure of the angle in consideration which is equal to 45°. Therefore, the value of tan inverse 1 is equal to 45°.
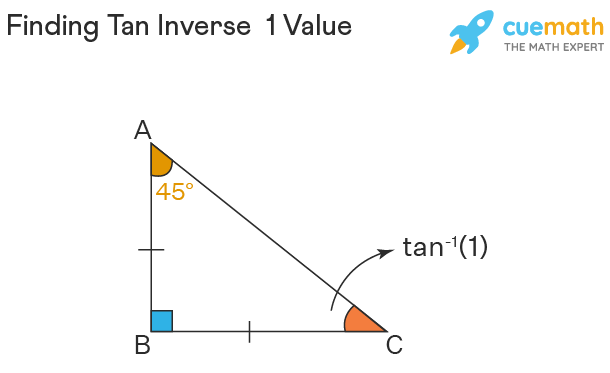
Arctan 1 in Degrees
As we evaluated the value of tan inverse 1 in the previous section, it can be written as tan-1(1) = 45°. Therefore, the value of arctan 1 in degrees is equal to 45 degrees. We can also prove it using the fact that the principal range interval of the tan inverse function is (-90°, 90°) and the tangent function is equal to 1 only when the angle is 45° within the range interval (-90°, 90°). So, tan x = 1 implies x = tan-1(1) ⇒ x = 45°. Hence, the tan inverse 1 value in degrees is equal to 45°.
Arctan 1 in Radians
Since we know that the range of principal value of tan is (-π / 2, π / 2) and the value of the tangent function is equal to 1 at π/4 radians, let us evaluate the value of arctan 1 in radians using these trigonometric facts.
Assume tan-1 (1) = θ
⇒ tan θ = 1 --- [Taking tan on both sides]
⇒ tan θ = tan (π / 4) ---- [Because tan (π / 4) = 1]
⇒ θ = π / 4 --- [Because the tangent function is equal to 1 only when the angle is π/4 radians within the principal range interval (-π / 2, π / 2) ]
Hence, the value of arctan 1 in radians is equal to π/4 radians.
Value of Tan Inverse 1 in Terms of Pi
Now that we know that the value of tan inverse 1 is equal to 45°, we will convert this value in radians using degrees to radians formula. We can say that to convert degrees into radians, we multiply the angle (in degrees) by π / 180. Therefore, the formula is,
Angle in Radians = Angle in Degrees × π / 180°
⇒ Arctan 1 in terms of π = 45° × π / 180°
= π/4 radians
Hence, the value of arctan 1 in terms of pi is equal to π/4 radians.
Important Notes on Arctan 1
- The value of arctan 1 in degrees is equal to 45°.
- The value of tan inverse 1 in radians is π/4 rad.
- We can find this value using the fact that tan 45° is equal to 1.
☛ Related Topics:
Arctan 1 Examples
-
Example 1: Find the value of arctan (1/2) + arctan (1/3). (Use the value of arctan 1)
Solution: Assume A = arctan (1/2) and B = arctan (1/3), then we have tan A = 1/2 and tan B = 1/3. Using the trigonometric identity of tangent function, we have
tan (A + B) = (tan A + tan B) / (1 - tanA tanB)
= (1/2 + 1/3) / (1 - 1/2 × 1/3)
= (5/6) / (1 - 1/6)
= (5/6) / (5/6)
= 1
⇒ tan (A + B) = 1
⇒ A + B = arctan (1)
⇒ arctan (1/2) + arctan (1/3) = arctan (1) --- [Because A = arctan (1/2) and B = arctan (1/3)]
= π/4 rad --- [Because the value of arctan 1 is equal to π/4 rad]
Answer: arctan (1/2) + arctan (1/3) = π/4 rad.
-
Example 2: Evaluate the value of tan inverse 1 by root 3.
Solution: We know that tan (π/6) = 1/√3 and π/6 lies in the principal value range of tan inverse which is (-π/2, π/2).
Therefore, we have tan (π/6) = 1/√3
⇒ tan-1(tan π/6) = tan-1(1/√3)
⇒ π/6 = tan-1(1/√3)
Answer: Value of tan inverse 1 by root 3 is π/6.
-
Example 3: Calculate the value of arctan (-1).
Solution: Assume A = arctan (-1), then we have tan A = -1. Now, the principal value range of the arctangent function is equal to (-π/2, π/2) and we know that arctan 1 = π/4. Using inverse trigonometry identity, we know that arctan (-x) = - arctan x. So, we have
arctan (-1) = - arctan 1
= - (π/4) --- [Because arctan 1 is equal to π/4]
= -π/4 which lies in the interval (-π/2, π/2)
Answer: arctan (-1) = -π/4
-
Example 4: Find the value of tan-1 (1) and tan-1 (tan 1).
Solution: To find the values of the above inverse trigonometric ratios, we will use trigonometric identities.
Let's find the values of inverse trigonometric ratios.
(i) Let tan-1 (1) = θ
⇒ tan θ = 1
Since we know that the range of principal value of tan is (-π / 2, π / 2)
Also we know that tan (π / 4) = 1
⇒ tan θ = tan (π / 4)
⇒ θ = π / 4
(ii) As we know that tan-1 (tan x) = x for x belongs to (- π / 2, π / 2)
⇒ tan-1 (tan 1) = 1
Answer: The value of tan-1 (1) is π / 4, and tan-1 (tan 1) is π / 4

FAQs on Arctan 1
What is the Value of Arctan 1?
The value of arctan 1 or tan inverse 1 is equal to π/4 radians or 45 degrees.
How Do You Find the Exact Value of Tan Inverse 1?
Since we know that the range of principal value of tan is (-π / 2, π / 2) and the value of the tangent function is equal to 1 at π/4 radians, therefore the value of tan inverse 1 is equal to π/4 radians.
Is Arctan 1 The Same as the Tan Inverse 1?
Yes, the value of arctan 1 is the same as tan inverse 1 which is 45 degrees. Arctan is another form of writing the inverse tangent function, which is also written as tan inverse (tan-1).
What is Arctan 1 in Degrees?
The value of arctan 1 is 45° in degrees.
What is Tan Inverse 1 in Radians?
The value of tan inverse 1 in radians is equal to π/4 rad.
What is Arctan 1 In Terms of Pi?
The value of tan inverse 1 is equal to π/4 rad in terms of pi.
What is the Value of Arctan 1 / √3?
We know that tan (π/6) = 1/√3 and π/6 lies in the principal value range of tan inverse which is (-π/2, π/2). So, arctan (1/√3) is equal to π/6 rad or 30°.
What is the Tan Inverse of Negative 1?
The value of tan inverse negative 1 is given by, tan-1(-1) = -tan-1(1) = -π/4 (because tan inverse 1 is equal to π/4).
visual curriculum