Cos 320 Degrees

The value of cos 320 degrees is 0.7660444. . .. Cos 320 degrees in radians is written as cos (320° × π/180°), i.e., cos (16π/9) or cos (5.585053. . .). In this article, we will discuss the methods to find the value of cos 320 degrees with examples.

• Cos 320°: 0.7660444. . .
• Cos (-320 degrees): 0.7660444. . .
• Cos 320° in radians: cos (16π/9) or cos (5.5850536 . . .)

What is the Value of Cos 320 Degrees?

The value of cos 320 degrees in decimal is 0.766044443. . .. Cos 320 degrees can also be expressed using the equivalent of the given angle (320 degrees) in radians (5.58505 . . .)

We know, using degree to radian conversion, θ in radians = θ in degrees × (pi/180°)
⇒ 320 degrees = 320° × (π/180°) rad = 16π/9 or 5.5850 . . .
∴ cos 320° = cos(5.5850) = 0.7660444. . .

Explanation:

For cos 320 degrees, the angle 320° lies between 270° and 360° (Fourth Quadrant). Since cosine function is positive in the fourth quadrant, thus cos 320° value = 0.7660444. . .
Since the cosine function is a periodic function, we can represent cos 320° as, cos 320 degrees = cos(320° + n × 360°), n ∈ Z.
⇒ cos 320° = cos 680° = cos 1040°, and so on.
Note: Since, cosine is an even function, the value of cos(-320°) = cos(320°).

Methods to Find Value of Cos 320 Degrees

The cosine function is positive in the 4th quadrant. The value of cos 320° is given as 0.76604. . .. We can find the value of cos 320 degrees by:

• Using Trigonometric Functions
• Using Unit Circle

Cos 320° in Terms of Trigonometric Functions

Using trigonometry formulas, we can represent the cos 320 degrees as:

• ± √(1-sin²(320°))
• ± 1/√(1 + tan²(320°))
• ± cot 320°/√(1 + cot²(320°))
• ±√(cosec²(320°) - 1)/cosec 320°
• 1/sec 320°

Note: Since 320° lies in the 4th Quadrant, the final value of cos 320° will be positive.

We can use trigonometric identities to represent cos 320° as,

• -cos(180° - 320°) = -cos(-140°)
• -cos(180° + 320°) = -cos 500°
• sin(90° + 320°) = sin 410°
• sin(90° - 320°) = sin(-230°)

Cos 320 Degrees Using Unit Circle

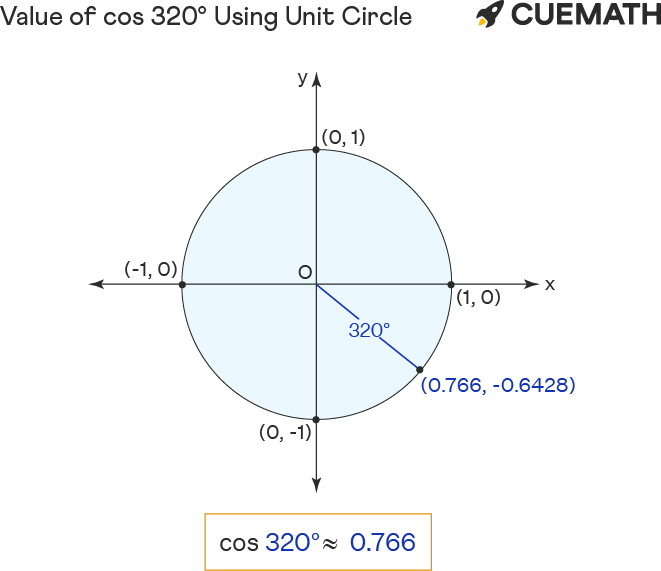
To find the value of cos 320 degrees using the unit circle:

• Rotate ‘r’ anticlockwise to form 320° angle with the positive x-axis.
• The cos of 320 degrees equals the x-coordinate(0.766) of the point of intersection (0.766, -0.6428) of unit circle and r.

Hence the value of cos 320° = x = 0.766 (approx)

☛ Also Check:

• cos 90 degrees
• cos 75 degrees
• cos 210 degrees
• cos 326 degrees
• cos 32 degrees
• cos 155 degrees

FAQs on Cos 320 Degrees

What is Cos 320 Degrees?

Cos 320 degrees is the value of cosine trigonometric function for an angle equal to 320 degrees. The value of cos 320° is 0.766 (approx)

What is the Value of Cos 320 Degrees in Terms of Sin 320°?

Using trigonometric identities, we can write cos 320° in terms of sin 320° as, cos(320°) = √(1 - sin²(320°)). Here, the value of sin 320° is equal to -0.6428.

How to Find the Value of Cos 320 Degrees?

The value of cos 320 degrees can be calculated by constructing an angle of 320° with the x-axis, and then finding the coordinates of the corresponding point (0.766, -0.6428) on the unit circle. The value of cos 320° is equal to the x-coordinate (0.766). ∴ cos 320° = 0.766.

How to Find Cos 320° in Terms of Other Trigonometric Functions?

Using trigonometry formula, the value of cos 320° can be given in terms of other trigonometric functions as:

• ± √(1-sin²(320°))
• ± 1/√(1 + tan²(320°))
• ± cot 320°/√(1 + cot²(320°))
• ± √(cosec²(320°) - 1)/cosec 320°
• 1/sec 320°

☛ Also check: trigonometry table

What is the Value of Cos 320° in Terms of Cosec 320°?

Since the cosine function can be represented using the cosecant function, we can write cos 320° as -[√(cosec²(320°) - 1)/cosec 320°]. The value of cosec 320° is equal to -1.55572.