30-60-90 Formula

We have different types of triangles existing such as an acute, obtuse, right triangle. Before understanding 30-60-90 formulas, let us first recall what is a 30-60-90 triangle. 30-60-90 is one of the special right triangles where the three interior angles measure 30°, 60°, and 90°. Right triangles with 30-60-90 interior angles are known as special right triangles i.e, their sides and angles are predictable and consistent.

• All 30-60-90 triangles are similar.
• Two 30-60-90 triangles sharing a long leg form an equilateral triangle.

Let us understand 30-60-90 Formula using solved examples in the following section.

What is the 30-60-90 Formula?

A 30-60-90 degree triangle is a special right triangle, so its side lengths are always consistent with each other. The ratio of the sides follow the 30-60-90 triangle ratio given by the 30-60-90 Formula as,

1  : √3 : 2

Thus, for a 30-60-90 triangle, the dimensions of the sides can be given as:

• y = Short side (opposite the 30° angle) 
• 2y = Hypotenuse (opposite the 90° angle) 
• y√3 = Long side (opposite the 60° angle) 

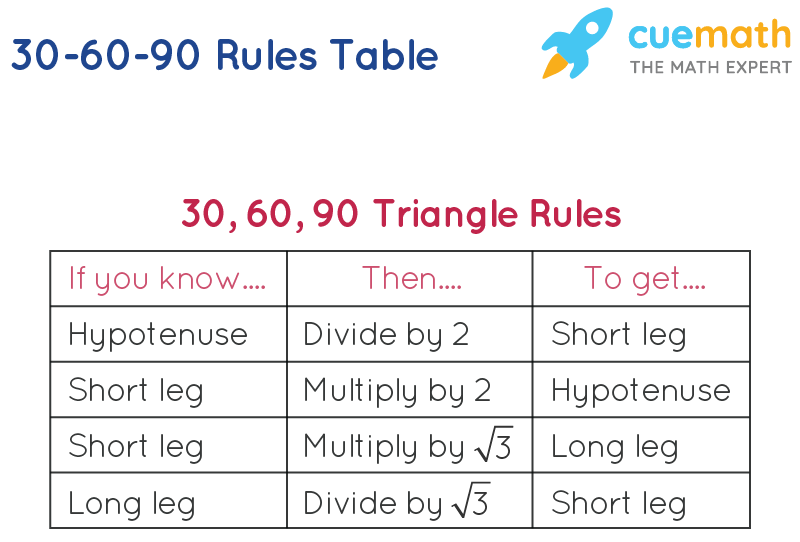
These three special rules can be considered the 30-60-90 triangle theorem and are unique to these special right triangles:

1. The hypotenuse (the triangle's longest side) is always twice the length of the short leg.
2. The length of the longer leg is the short leg's length times √3.
3. If you know the length of any one side of a 30-60-90 triangle, you can find the missing side lengths.

Let's solve some examples using 30-60-90 Formula

Examples Using 30-60-90 Formula

Example 1: For the given right triangle the value of the hypotenuse is 3.46km. Find all the other sides of the triangle using 30-60-90 Formula.

Solution:

Let the hypotenuse, base, and height be 2x, x, and x√3. Using 30-60-90 Formula,

Hypotenuse = 2x = 3.46km

Base = x = 3.46/2 = 1.73km

Height = x√3 = √3 × 1.73 = 3km

Answer: Thus, the dimensions are 3.46km, 1.73km and 3km.

Example 2: Find the missing side of the given triangle.

Solution:

We can see that it's a right triangle in which the hypotenuse is the double of one of the sides of the triangle. Thus, it is called a 30-60-90 triangle where the smaller angle will be 30.

Using 30-60-90 Formula, the longer side is always opposite to 60° and the missing side measures 3√3 units in the given figure.

Answer: Thus, the missing side is 3√3 units.