Derivative of Root x

The derivative of root x is equal to (1/2) x^-1/2. We can calculate this derivative using various methods of differentiation such as the first principle of derivatives, power rule of differentiation, and chain rule method. Mathematically, we can write the formula for the derivative of root x as d(√x)/dx = (1/2) x^-1/2 or 1(/2√x). The formula for the power rule of derivatives is d(xⁿ)/dx = n x^n-1, where n ≠ -1. Using this formula and substituting n = 1/2, we can get the derivative of root x.

Further, in this article, we will explore the derivative of root x and its formula using different methods of evaluating derivatives. We will also solve various examples related to the derivative of root x and other combinations of functions with root x for a better understanding of the concept.

The derivative of root x is given by, d(√x)/dx = (1/2) x^-1/2 or 1/(2√x). As we know, the derivative of a function in mathematics is the process of finding the rate of change of a function with respect to a variable. The derivative of root x can be determined using the power rule of differentiation and the first principle of derivatives. We can also use the derivative of root x along with the chain rule method for evaluating the derivatives of square root functions. In the next section, let us understand the formula for this derivative.

The formula for the derivative of root x is given by d(√x)/dx (OR) (√x)' = (1/2) x^-1/2 (OR) 1/(2√x), i.e.,

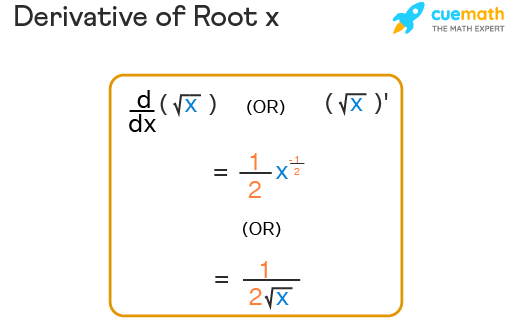
We can evaluate the above formula for the derivative of root x using the following methods:

• First Principle of Derivatives
• Power Rule of Differentiation

Now that we know that the derivative of root x is equal to (1/2) x^-1/2, we will prove it using the first principle of differentiation. For a function f(x), its derivative according to the definition of limits, that is, the first principle of derivatives is given by the formula f'(x) = lim _h→0 [f(x + h) - f(x)] / h. We will also rationalization method to simplify the expression. Therefore, we have

d(√x)/dx = lim _h→0 [√(x + h) - √x] / h

To simplify the expression, multiply the numerator and denominator of the above expression by √(x + h) + √x.

lim _h→0 [√(x + h) - √x] / h = lim _h→0 { [√(x + h) - √x] × [√(x + h) + √x ] } / { h × [√(x + h) + √x ] }

= lim _h→0 [(x + h) - x] / { h × [√(x + h) + √x ] } --- (Using (a+b) (a-b) = a² - b² formula)

= lim _h→0 [x + h - x] / { h × [√(x + h) + √x ] }

= lim _h→0 h / { h × [√(x + h) + √x ] }

= lim _h→0 1 / [√(x + h) + √x ]

= 1/(√x + √x)

= 1/(2√x)

Hence, we have proved the formula for the derivative of root x.

Now, the formula for the power rule of derivatives is given by, d(xⁿ)/dx = nx^n-1, where n ≠ -1. Root x is an exponential function with x as the base and 1/2 as the power. Now, if we substitute n = 1/2 in the formula d(xⁿ)/dx = nx^n-1, where n ≠ -1, then we have

d(x^1/2)/dx = (1/2) x^{(1/2) - 1}

= (1/2) x^-1/2

= 1/(2√x)

Therefore, we have proved that the derivative of root x is equal to 1/(2√x).

One of the important applications of the derivative of root x is to find the derivative of square root functions. We can apply the chain rule method of differentiation to find the derivatives of square root function along with using the derivative of root x. Let us solve an example to understand its application.

Example: Find the derivative of √(2x + 5).

Solution: To find the derivative of √(2x + 5), we will use the chain rule method and use the formula of the derivative of root x.

d(√(2x + 5))/dx = d(√(2x + 5))/d(2x + 5) × d(2x + 5)/dx

= 1/(2√(2x + 5)) × 2

= 2/(2√(2x + 5))

= 1/√(2x + 5)

Important Notes on Derivative of Root x

• The derivative of root x is given by d(√x)/dx = (1/2) x^-1/2 or 1/(2√x).
• Root x given by √x is an exponential function with x as the variable and base as 1/2.
• We can calculate the derivative of root x using the Power Rule and First Principle of Derivatives.

☛ Related Topics:

• Integration of Root x
• Derivative of xsinx
• Derivative of Sin3x

What is Derivative of Root x in Calculus?

The derivative of root x is equal to (1/2) x^-1/2. We can calculate this derivative using various methods of differentiation such as the first principle of derivatives, power rule of differentiation, and chain rule method.

What is the Formula for the Derivative of Root x?

The formula for the derivative of root x is given by d(√x)/dx (OR) (√x)' = (1/2) x^-1/2 (OR) 1/(2√x)

How To Find The Derivative of Root x?

The derivative of root x can be determined using the power rule of differentiation and the first principle of derivatives.

What is the Second Derivative of Root x?

The second derivative of root x is (-1/4) x^-3/2. We can calculate the second derivative of root x by differentiating the first derivative of root x.

How to Find the Derivative of 1 by Root x?

We can evaluate the derivative of 1 by root x using the power rule of differentiation and it is given by, d(1/√x)/dx = (-1/2) x^{-1/2 - 1} = (-1/2) x^-3/2

How To Find The Derivative of Root x Minus 1?

The derivative of root x minus 1 can be calculated using the power rule of differentiation. The formula for the derivative of root x minus 1 is given by, d(√(x - 1))/dx = 1/(2√(x - 1)).