Hyperbolic Functions
Hyperbolic functions are defined in mathematics in a way similar to trigonometric functions. As the name suggests, the graph of a hyperbolic function represents a rectangular hyperbola, and its formula can often be seen in the formulas of a hyperbola. They are defined using a hyperbola instead of a unit circle as in the case of trigonometry. Hyperbolic functions are analogous to trigonometric functions but are derived from a hyperbola as trigonometric functions are derived from a unit circle.
Hyperbolic functions are expressed in terms of the exponential function ex. There are six hyperbolic functions are sinh x, cosh x, tanh x, coth x, sech x, csch x. In this article, we will define these hyperbolic functions and their properties, graphs, identities, derivatives, etc. along with some solved examples.
What are Hyperbolic Functions?
As an ordinary trigonometric function is defined for or on a circle, similarly a hyperbolic function is defined for a hyperbola. In ordinary trigonometry, we were using sine, cosine, and other functions. Similarly, for hyperbolic functions, we use sinh, cosh, tanh, coth, sech, and csch. As in ordinary trigonometric function, we know that the coordinates of points on the unit circle are (cos θ, sin θ), similarly in hyperbolic functions, (cosh θ, sinh θ) forms right half of equilateral hyperbola.
These functions can be solutions of various linear differential equations, cubic equations, and Laplace's equation. The six basic hyperbolic functions are:
- Hyperbolic sine or sinh x
- Hyperbolic cosine or cosh x
- Hyperbolic tangent or tanh x
- Hyperbolic cosecant or cosech x
- Hyperbolic secant or sech x
- Hyperbolic cotangent or coth x
Hyperbolic Meaning
Hyperbolic functions are defined analogously to trigonometric functions. We have main six hyperbolic functions, namely sinh x, cosh x, tanh x, coth x, sech x, and cosech x. They can be expressed as a combination of the exponential function. These functions are derived using the hyperbola just like trigonometric functions are derived using the unit circle.
Hyperbolic Functions Formulas
The hyperbolic functions are defined through the algebraic expressions that include the exponential function (ex) and its inverse exponential functions (e-x), where e is the Euler’s constant. Let us see all their formulas one by one:
- Sinh x: This is the odd part of the exponential functions. An algebraic expression for hyperbolic sine function is:
sinh x = (ex - e-x)/2 - Cosh x: This is the even part of the exponential function. Algebraic expression for hyperbolic cosine function is:
cosh x = (ex + e-x)/2 - Tanh x: tanh x = sinh x/cosh x = (ex - e-x)/(ex + e-x)
- Coth x: coth x = cosh x/sinh x = (ex + e-x)/(ex - e-x)
- Sech x: sech x = 1/cosh x = 2/(ex + e-x)
- Csch x: csch x = 2/(ex - e-x)
Hyperbolic Functions Graphs
The graph of a hyperbolic function synonymous with its name represents a rectangular hyperbola and its formula can often be seen in the formulas of a hyperbola. Chart of graphs of different hyperbolic functions is given below:
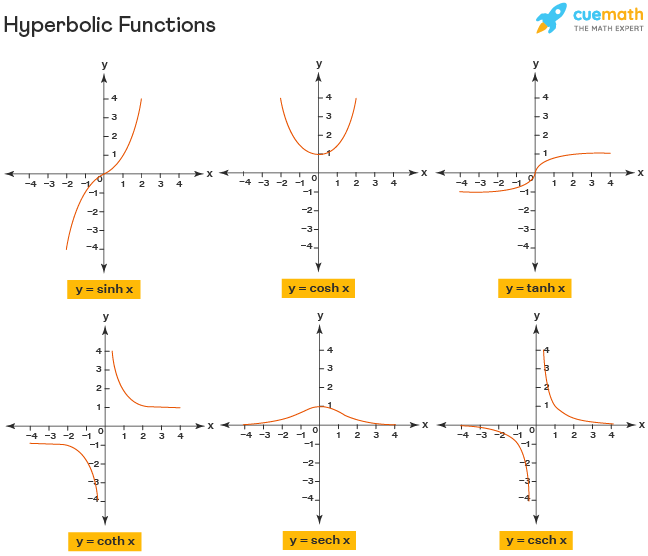
Domain and Range of Hyperbolic Functions
Looking at the graph of a hyperbolic function, we can determine its domain and range. The domains and ranges of these functions are summarized in the following table:
| Hyperbolic Function | Domain | Range |
|---|---|---|
| sinh x | (-∞ , + ∞) | (-∞ , + ∞) |
| cosh x | (-∞ , + ∞) | [1, ∞) |
| tanh x | (-∞ , + ∞) | (-1, 1) |
| coth x | (-∞ , 0) U (0 , + ∞) | (-∞ , - 1) U (1 , +∞) |
| sech x | (-∞ , + ∞) | (0 , 1] |
| csch x | (-∞ , 0) U (0 , +∞) | (-∞ , 0) U (0 , +∞) |
Properties of Hyperbolic Functions
The properties of hyperbolic functions are analogous to the properties of trigonometric functions. Let us go through some of the important properties of these functions which are used to solve various problems in mathematics.
- sinh (-x) = – sinh(x)
- cosh (-x) = cosh (x)
- tanh (-x) = - tanh x
- coth (-x) = - coth x
- sech (-x) = sech x
- csc (-x) = - csch x
- cosh 2x = 1 + 2 sinh2(x) = 2 cosh2x - 1
- cosh 2x = cosh2x + sinh2x
- sinh 2x = 2 sinh x cosh x
Hyperbolic functions can also be deduced from trigonometric functions with complex arguments:
- sinh x = - i sin(ix)
- cosh x = cos(ix)
- tanh x = - i tan(ix)
- coth x = i cot(ix)
- sech x = sec(ix)
Hyperbolic Trig Identities
The hyperbolic trig identities are similar to trigonometric identities and can be understood better from below. Osborn's rule states that trigonometric identities can be converted into hyperbolic trig identities when expanded completely in terms of integral powers of sines and cosines, which includes changing sine to sinh, cosine to cosh. The sign of every term that contains a product of two sinh should be replaced.
- sinh x – sinh y = 2 cosh [(x+y)/2] sinh [(x-y)/2]
- sinh x + sinh y = 2 sinh [(x+y)/2] cosh[(x-y)/2]
- cosh x + cosh y = 2 cosh [(x+y)/2] cosh[(x-y)/2]
- cosh x – cosh y = 2 sinh [(x+y)/2] sinh [(x-y)/2])
- 2 sinh x cosh y = sinh (x + y) + sinh (x - y)
- 2 cosh x sinh y = sinh (x + y) – sinh (x – y)
- 2 sinh x sinh y = cosh (x + y) – cosh (x – y)
- 2 cosh x cosh y = cosh (x + y) + cosh (x – y)
- sinh(x ± y) = sinh x cosh y ± coshx sinh y
- cosh(x ± y) = cosh x cosh y ± sinh x sinh y
- tanh(x ± y) = (tanh x ± tanh y)/ (1± tanh x tanh y)
- coth(x ± y) = (coth x coth y ± 1)/(coth y ± coth x)
- cosh2x - sinh2x = 1
- tanh2x + sech2x = 1
- coth2x - csch2x = 1
Hyperbolic Function Integrals and Derivatives
The derivative and integral of a hyperbolic function are similar to the derivative and integral of a trigonometric function. Unlike the derivative of trigonometric functions, we can observe the change in sign in the derivative of the hyperbolic secant function. The derivatives and integrals of the hyperbolic functions are summarized in the following table:
| Hyperbolic Function | Derivative | Integral |
|---|---|---|
| sinh x | cosh x | cosh x + C |
| cosh x | sinh x | sinh x + C |
| tanh x | sech2x | ln(cosh x) + C |
| coth x | -csch2x | ln(sinh x) + C |
| sech x | -sech x. tanh x | arctan(sinh x) + C |
| csch x | -csch x. coth x | ln(tanh (x/2)) + C |
Inverse Hyperbolic Functions
The inverse of a hyperbolic function is called an inverse hyperbolic function. For example, if x = sinh y, then y = sinh-1 x is the inverse of the hyperbolic sine function. The inverse hyperbolic functions expressed in terms of logarithmic functions are shown below:
- sinh-1x = ln (x + √(x2 + 1))
- cosh-1x = ln (x + √(x2 - 1))
- tanh-1x = ln [(1 + x)/(1 - x)]
- coth-1x = ln [(x + 1)/(x - 1)]
- sech-1x = ln [{1 + √(1 - x2)}/x]
- csch-1x = ln [{1 + √(1 + x2)}/x]
Important Notes on Hyperbolic Functions
- There are six hyperbolic functions, namely sinh x, cosh x, tanh, x, coth x, sech x, csch x.
- A hyperbolic function is defined for a hyperbola.
- The hyperbolic identities are analogous to trigonometric identities.
Related Topics
Hyperbolic Functions Examples
-
Example 1: Find the value of x if 3 sinh x - 2 cosh x - 2 = 0 using hyperbolic function formula.
Solution: We know that sinh x = (ex - e-x)/2 and cosh x = (ex + e-x)/2
Substitute these values in the given equation, we have
3 sinh x - 2 cosh x - 2 = 0
⇒ 3 [(ex - e-x)/2] - 2 [(ex + e-x)/2] - 2 = 0
⇒ 3 (ex - e-x) - 2 (ex + e-x) - 4 = 0
⇒ 3 ex - 3 e-x - 2 ex - 2 e-x - 4 = 0
⇒ ex - 5 e-x - 4 = 0
⇒ (ex)2 - 5 - 4 ex = 0
⇒ (ex)2 - 5 - 5 ex + ex = 0
⇒ ex (ex + 1) - 5(ex + 1) = 0
⇒ (ex - 5)(ex + 1) = 0
Since
ex ≠ −1, therefore we have ex = 5 ⇒ x = ln 5
Answer: x = ln 5 if 3 sinh x - 2 cosh x - 2 = 0
-
Example 2: Show that cosh x + sinh x = ex using hyperbolic functions formulas.
Solution: We know that sinh x = (ex - e-x)/2 and cosh x = (ex + e-x)/2
LHS = cosh x + sinh x
= (ex - e-x)/2 + (ex + e-x)/2
= (ex - e-x + ex + e-x)/2
= 2ex / 2
= ex = RHS
Answer: Hence we proved that cosh x + sinh x = ex
-
Example 3: Prove the hyperbolic trig identity coth2x - csch2x = 1.
Solution: To prove the identity coth2x - csch2x = 1, we will use the following hyperbolic functions formulas:
- coth x = cosh x/sinh x
- csch x = 1/sinh x
Consider LHS = coth2x - csch2x
= (cosh x/sinh x)2 - (1/sinh x)2
= cosh2x/sinh2x - 1/sinh2x
= (cosh2x - 1)/sinh2x
= sinh2x/sinh2x --- [Using identity cosh2x - sinh2x = 1 ⇒ cosh2x - 1 = sinh2x]
= 1
= RHS
Answer: We have proved the hyperbolic trig identity coth2x - csch2x = 1.

FAQs on Hyperbolic Functions
What are Hyperbolic Functions in Math?
Hyperbolic functions are defined for a hyperbola. The graph of a hyperbolic function synonymous with its name represents a rectangular hyperbola and the hyperbolic function formula can often be seen in the formulas of a hyperbola. Hyperbolic functions are analogous to trigonometric functions but are derived from a hyperbola as trigonometric functions are derived from a unit circle.
What are the Main Six Hyperbolic Functions?
There are six hyperbolic functions, namely:
- Hyperbolic Sine, sinh x
- Hyperbolic Cosine, cosh x
- Hyperbolic Tangent, tanh x
- Hyperbolic Cotangent, coth x
- Hyperbolic Secant, sech x
- Hyperbolic Cosecant, csch x
What are the Formulas of Hyperbolic Functions Formula?
The formulas for main hyperbolic functions are:
- sinh x = (ex - e-x)/2
- cosh x = (ex + e-x)/2
- tanh x = (ex - e-x)/(ex + e-x)
- coth x = (ex + e-x)/(ex - e-x)
- sech x = 2/(ex + e-x)
- csch x = 2/(ex - e-x)
What is the Differentiation of Hyperbolic Functions?
The derivatives of hyperbolic functions are:
- d(sinh x)/dx = cosh x
- d(cosh x)/dx = sinh x
- d(tanh x)/dx = sech2x
- d(coth x)/dx = - cosech2x
- d(sech x)/dx = - sech x.tanh x
- d(cosech x)/dx = - cosech x.coth x
What are Inverse Hyperbolic Functions?
The list of inverse hyperbolic functions is:
- sinh-1x = ln (x + √(x2 + 1))
- cosh-1x = ln (x + √(x2 - 1))
- tanh-1x = ln [(1 + x)/(1 - x)]
- coth-1x = ln [(x + 1)/(x - 1)]
- sech-1x = ln [{1 + √(1 - x2)}/x]
- csch-1x = ln [{1 + √(1 + x2)}/x]
How many Hyperbolic Functions are there?
There are main six hyperbolic functions, namely sinh x, cosh x, tanh x, coth x, sech x, csch x.
What are Hyperbolic Trig Identities?
The hyperbolic trig identities are formulas of hyperbolic functions which are analogous to trigonometric functions. Some of the hyperbolic trig identities are:
- sinh(x ± y) = sinh x cosh y ± coshx sinh y
- cosh(x ± y) = cosh x cosh y ± sinh x sinh y
- tanh(x ± y) = (tanh x ± tanh y)/ (1± tanh x tanh y)
- coth(x ± y) = (coth x coth y ± 1)/(coth y ± coth x)
- cosh2x - sinh2x = 1
- tanh2x + sech2x = 1
- coth2x - csch2x = 1
- sinh x – sinh y = 2 cosh [(x+y)/2] sinh [(x-y)/2]
- sinh x + sinh y = 2 sinh [(x+y)/2] cosh[(x-y)/2]
- cosh x + cosh y = 2 cosh [(x+y)/2] cosh[(x-y)/2]
- cosh x – cosh y = 2 sinh [(x+y)/2] sinh [(x-y)/2])
- 2 sinh x cosh y = sinh (x + y) + sinh (x - y)
- 2 cosh x sinh y = sinh (x + y) – sinh (x – y)
- 2 sinh x sinh y = cosh (x + y) – cosh (x – y)
- 2 cosh x cosh y = cosh (x + y) + cosh (x – y)
Why are Hyperbolic Functions Called Hyperbolic?
Hyperbolic functions are called hyperbolic because they are derived and defined from a hyperbola just like trigonometric functions are derived from a unit circle. The graph of a hyperbolic function represents a rectangular hyperbola.
What is the Difference Between Hyperbolic Functions and Trigonometric Functions?
The basic difference between trigonometric and hyperbolic functions is that trigonometric functions are defined from a unit circle x2 + y2 = 1 and hyperbolic functions are derived from a hyperbola x2 - y2 = 1. Another difference between them is that hyperbolic functions are not periodic as trigonometric functions are.
visual curriculum