Integral of Sin 3x
Integral of sin 3x is given by (-1/3) cos 3x + C. The integral of sin 3x is called the anti-derivative of sin 3x as integration is the reverse process differentiation. Sin 3x is an important trigonometric formula that is used to solve various problems in trigonometry. The integral of sin 3x can be calculated using the substitution method and using the sin 3x formula.
In this article, we will calculate the integral of sin 3x, prove it using the substitution method and sin 3x formula and determine the definite integral of sin 3x using different limits.
What is Integral of Sin 3x?
The integral of sin 3x can be calculated using the formula for the integral of sin ax which is given by ∫sin (ax) dx = (-1/a) cos ax + C. Mathematically, the integral of sin 3x is written as ∫sin 3x dx = (-1/3) cos 3x + C, where C is the constant of integration, dx denotes that the integration of sin 3x is with respect to x, ∫ is the symbol for integration. The integral of sin 3x can also be evaluated using the substitution method and sin 3x formula.
Integral of Sin 3x Formula
Sin 3x formula is given by sin 3x = 3 sin x - 4 sin3x and the formula for the integral of sin 3x is given by, ∫sin 3x dx = (-1/3) cos 3x + C, where C is the constant of integration.
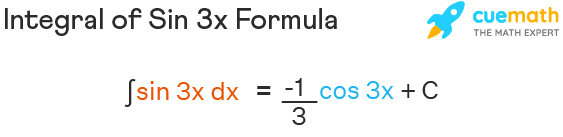
Integral of Sin 3x Using Substitution Method
Now, we know that the integral of sin 3x is (-1/3) cos 3x + C, where C is the constant of integration. Let us prove this using the substitution method. We will use the following formulas of integration and differentiation:
- ∫sin x dx = -cos x + C
- d(ax)/dx = a
Assume 3x = u, then differentiating 3x = u with respect to x, we have 3dx = du ⇒ dx = (1/3)du. Using the above formulas, we have
∫sin 3x dx = ∫sin u (du/3)
⇒ ∫sin 3x dx = (1/3) ∫sin u du
⇒ ∫sin 3x dx = (1/3) (-cos u + C) [Because ∫sin x dx = -cos x + C]
⇒ ∫sin 3x dx = (-1/3) cos u + C/3
⇒ ∫sin 3x dx = (-1/3) cos 3x + K, where K = C/3
Hence, we have derived the integral of sin 3x using the substitution method.
Integral of Sin 3x Using Sin 3x Formula
We know that the sin 3x formula is sin 3x = 3 sin x - 4 sin3x. Next, we will prove that the integration of sin 3x is given by (-1/3) cos 3x + C using the sin 3x formula. Before proving the integral of sin 3x, we will derive the integral of sin cube x, that is, sin3x. We will use the following formulas to prove the integral of sin3x:
- cos2x + sin2x = 1 ⇒ sin2x = 1 - cos2x
- ∫sin x dx = -cos x dx
∫sin3x dx = ∫sin x. sin2x dx
= ∫sin x.(1 - cos2x) dx
= ∫sin x dx - ∫sin x. cos2x dx --- (1)
= I1 - I2 , where I1 = ∫sin x dx and I2 = ∫sin x. cos2x dx
Now, I1 = ∫sin x dx = -cos x + C1, where C1 is the constant of integration ---- (2)
For I2 = ∫sin x. cos2x dx, assume cos x = u ⇒ -sin x dx = du ⇒ sin x dx = -du
I2 = ∫sin x. cos2x dx
= ∫u2 (-du)
= - ∫u2 du
= - u3/3 + C2, where C2 is the constant of integration
= (-1/3) cos3x + C2 ---- (3)
Subsitute the values from (2) and (3) in (1),
∫sin3x dx = (-cos x + C1) - ((-1/3) cos3x + C2)
= -cos x + (1/3) cos3x + C1 - C2
= -cos x + (1/3) cos3x + C, where C = C1 - C2
⇒ ∫sin3x dx = -cos x + (1/3) cos3x + C --- (4)
Now that we have derived the integral of sin3x, we will use this formula along with some other formulas to derive the integral of sin 3x:
- ∫sin x dx = -cos x dx
- ∫sin3x dx = -cos x + (1/3) cos3x + C
- sin 3x = 3 sin x - 4 sin3x
- cos 3x = 4cos3x - 3 cos x
Using the above formulas, we have
∫sin 3x dx = ∫(3 sin x - 4 sin3x) dx
= 3 ∫sin x dx - 4 ∫sin3x dx
= 3(-cos x) - 4(-cos x + (1/3) cos3x) + C, where C is the constant of integration
= -3 cos x + 4 cos x - (4/3)cos3x + C
= cos x - (4/3)cos3x + C
= (1/3)(3cos x - 4cos3x + 3C)
= (1/3)(-cos 3x + 3C) [Because cos 3x = 4cos3x - 3 cos x]
= (-1/3) cos 3x + C
Hence, we have derived the integration of sin 3x using the sin 3x formula.
Definite Integral of Sin 3x
We have proved that the integral of sin 3x is (-1/3) cos 3x + C. Now, we will determine the values of the definite integral of sin 3x with different limits. First, we will take the limits from 0 to π/3.
Definite Integral of Sin 3x From 0 to π/3
\(\begin{align}\int_{0}^{\frac{\pi}{3}}\sin 3x \ dx &= \left [ -\frac{1}{3}\cos 3x+C \right ]_0^\frac{\pi}{3}\\&=\left ( -\frac{1}{3}\cos 3\frac{\pi}{3}+C \right )-\left ( -\frac{1}{3}\cos 3(0)+C\right )\\&=-\frac{1}{3}\cos \pi+C + \frac{1}{3}\cos 0-C\\&= -\frac{1}{3}(-1)+\frac{1}{3}(1)\\&=\frac{2}{3}\end{align}\)
Hence the value of the definite integral of sin 3x with limits from 0 to π/3 is equal to 2/3.
Definite Integral of Sin 3x From 0 to Pi
\(\begin{align}\int_{0}^{\pi}\sin 3x \ dx &= \left [ -\frac{1}{3}\cos 3x+C \right ]_0^\pi\\&=\left ( -\frac{1}{3}\cos 3\pi+C \right )-\left ( -\frac{1}{3}\cos 3(0)+C\right )\\&=-\frac{1}{3}\cos 3\pi+C + \frac{1}{3}\cos 0-C\\&= -\frac{1}{3}(-1)+\frac{1}{3}(1)\\&=\frac{2}{3}\end{align}\)
Hence the value of the definite integral of sin 3x with limits from 0 to π is equal to 2/3.
Definite Integral of Sin 3x From 0 to Pi/2
\(\begin{align}\int_{0}^{\frac{\pi}{2}}\sin 3x \ dx &= \left [ -\frac{1}{3}\cos 3x+C \right ]_0^\frac{\pi}{2}\\&=\left ( -\frac{1}{3}\cos 3\frac{\pi}{2}+C \right )-\left ( -\frac{1}{3}\cos 3(0)+C\right )\\&=-\frac{1}{3}\cos \frac{3\pi}{2}+C + \frac{1}{3}\cos 0-C\\&= -\frac{1}{3}(0)+\frac{1}{3}(1)\\&=\frac{1}{3}\end{align}\)
Hence the value of the definite integration of sin 3x with limits from 0 to π/2 is equal to 1/3.
Important Notes on Integral of Sin 3x
- The easiest way to determine the integral of sin 3x is using the formula ∫sin (ax) dx = (-1/a) cos ax + C.
- The integral of sin 3x is (-1/3) cos 3x + C and the integral of sin cube x is ∫sin3x dx -cos x + (1/3) cos3x + C.
Related Topics
Integral of Sin 3x Examples
-
Example 1: Determine the integral of sin 3x cosec 3x.
Solution: We know that sin x =1/cosec x and cosec x = 1/sin x, so we have
∫sin 3x cosec 3x dx = ∫sin (1/sin 3x) dx
= ∫1dx
= x + C
Answer: Hence the integral of sin 3x cosec 3x is x + C.
-
Example 2: Evaluate the integral of sin 3x ecos 3x.
Solution: To evaluate the integral of sin 3x ecos 3x, we will assume cos 3x = u.
Differentiating cos 3x = u with respect x, we get
-3 sin 3x dx = du
⇒ sin 3x = (-1/3) du
We have,
∫sin 3x ecos 3x dx = ∫(-1/3)eu du
= (-1/3) ∫eu du
= (-1/3) eu + C
= (-1/3) ecos 3x + C
Answer: Hence, the integral of sin 3x ecos 3x is (-1/3) ecos 3x + C.

FAQs on Integral of Sin 3x
What is Integral of Sin 3x in Trigonometry?
In trigonometry, the integral of sin 3x is written as ∫sin 3x dx = (-1/3) cos 3x + C, where C is the constant of integration.
How to Find the Integral of Sin 3x?
The integral of sin 3x can be calculated using the formula for the integral of sin ax which is given by ∫sin (ax) dx = (-1/a) cos ax + C. It can also be calculated using the substitution method and sin 3x formula.
What is the Definite Integral of Sin 3x from 0 to pi?
The value of the definite integral of sin 3x with limits from 0 to π is equal to 2/3.
What is the Integration of Sin3x?
The integral of sin cube x is given by ∫sin3x dx = -cos x + (1/3) cos3x + C.
What is the Integral of Sin 2x?
The integral of sin 2x dx is written as ∫ sin 2x dx = -(cos 2x)/2 + C, where C is the integration constant.
visual curriculum