Integration of Tan Square x
The formula for the integration of tan square x is tan x - x + C, with C as the integration constant. As we know that integration is nothing but the reverse process of differentiation, we can say that integration of tan square x is the same as the antiderivative of tan square x. We can determine the integral of tan2x using the trigonometric identity or by writing tan x in terms of sin x and cos x. Mathematically, we write the integration of tan square x as ∫ tan2x dx = tan x - x + C.
Let us calculate the integration of tan square x, determine its formula and the definite integral of tan square x with different limits. We will also solve some examples determining the integration of tan square x combined with some other trigonometric functions for a better understanding of the concept.
What is Integration of Tan Square x?
Integration of tan square x is the process of reverse differentiation of tan square x and finding its antiderivative. To find the integral of tan square x, we can use the trigonometric identities such as tan x = sin x/cos x and 1 + tan2x = sec2x. Mathematically, we can write the integration of tan square x as ∫ tan2x dx = tan x - x + C, where ∫ is the symbol of integration and C is the integration constant. Let us now go through the formula of the integration of tan square x.
Integration of Tan Square x Formula
Now, let us understand the formula of integral of tan2x. We can write the integration of tan square x mathematically as ∫ tan2x dx = tan x - x + C, where C is the integration constant. We will understand how to get this formula further in this article by proving the integral of tan square x. The integration of tan square x is the tangent of angle x minus x plus the constant of integration which is given symbolically in the image below:
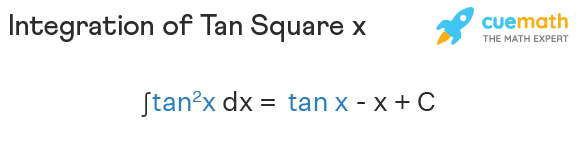
Integration of Tan Square x Proof
Now we know that the integration of tan square x is tan x - x + C which we will prove now using trigonometric identity sin2x + cos2x = 1. We will write tan x as sin x/ cos x. Therefore, we have
∫ tan2x dx = ∫ (sin x/ cos x)2 dx
= ∫ (sin2x / cos2x) dx
= ∫ (1 - cos2x)/cos2x dx [Because sin2x + cos2x = 1 ⇒ sin2x = 1 - cos2x]
= ∫ (1/cos2x) dx - ∫ 1 dx
= ∫ sec2x dx - ∫ dx
= tan x - x + C [Because the derivative of tan x is sec2x ⇒ integral of sec2x is tan x + K]
We can also prove the integration of tan square x using the trigonometric identity 1 + tan2x = sec2x. To evaluate, we have
∫ tan2x dx = ∫ (sec2x - 1) dx
= ∫ sec2x dx - ∫1dx
= tan x - x + C
Hence, we have proved that the integration of tan square x is tan x - x + C.
Integration of Tan Square x From 0 to Pi by 4
We know that the formula for the integration of tan square x is tan x - x + C. Next, we will find its definite integral with limits from 0 to π/4 using this formula. For this, we have
\(\begin{align}\int_{0}^{\frac{\pi}{4}} \tan^2x \ dx&=\left [ \tan x - x + C \right ]_0^\frac{\pi}{4}\\&=\tan \frac{\pi}{4} - \frac{\pi}{4}+C - \tan 0+0-C\\&=1-\frac{\pi}{4}\end{align}\)
Hence the integration of tan square x from 0 to pi by 4 is equal to 1 - π/4.
Important Notes on Integration of Tan Square
- The formula for the integration of tan square x is tan x - x + C.
- We can determine the integral of tan2x using the trigonometric identities such as sin2x + cos2x = 1 and 1 + tan2x = sec2x.
- The integration of tan square x from 0 to pi by 4 is equal to 1 - π/4.
☛ Related Topics:
Integration of Tan Square x Examples
-
Example 1: Find the integration of tan square x sec square x.
Solution: We will find the integration of tan square x sec square x using the substitution method.
Assume u = tan x ⇒ du = sec2x dx
∫tan2x sec2x dx = ∫u2 du
= u3/3 + C
= (1/3) tan3x + C
Answer: ∫tan2x sec2x dx = (1/3) tan3x + C
-
Example 2: Evaluate the integration of tan square x minus cot square x.
Solution: To find the integration of tan square x minus cot square x, we will use trigonometric identities
- 1 + tan2x = sec2x
- 1 + cot2x = cosec2x
We have,
∫(tan2x - cot2x) dx = ∫[(sec2x - 1) - (cosec2x - 1)] dx
= ∫(sec2x - 1 - cosec2x + 1) dx
= ∫(sec2x - cosec2x) dx
= ∫sec2x dx + ∫(- cosec2x) dx
= tan x + cot x + C [Because d(tan x)/dx = sec2x and d(cot x)/dx = - cosec2x]
Answer: Hence, ∫(tan2x - cot2x) dx = tan x + cot x + C

FAQs on Integration of Tan Square x
What is the Integration of Tan Square x in Calculus?
Integration of tan square x is the process of reverse differentiation of tan square x and finding its antiderivative. Mathematically, we can write the integration of tan square x as ∫ tan2x dx = tan x - x + C.
What is the Formula for Integration of Tan Square x?
The formula for the integration of tan square x is tan x - x + C, with C as the integration constant.
How to Find Integration of Tan Square x?
We can determine the integral of tan2x using the trigonometric identities such as sin2x + cos2x = 1 and 1 + tan2x = sec2x.
What is Integration of Tan Square x Sec Square x?
The integration of Tan Square x Sec Square x is given by, ∫tan2x sec2x dx = (1/3) tan3x + C.
How to Find the Integration of Tan Square x Minus Cot Square x?
The Integration of Tan Square x Minus Cot Square x is written as ∫(tan2x - cot2x) dx = tan x + cot x + C.
What is the Integration of Tan Square x Minus Sin Square x?
The Integration of Tan Square x Minus Sin Square x is given by, ∫(tan2x - sin2x) dx = tan x - (3/2)x + (1/4) sin 2x + C.
visual curriculum