Cos Inverse Formula

Inverses of a trigonometric function are used to find the angle of a triangle. Cos inverse formula is used to find the angle when base and hypotenuse are given. Cos inverse function also possesses some properties regarding its domain and range. Its domain is [-1,1] and its range is from 0 to \(\dfrac{\pi}{2}\). Let us understand the cos inverse formula using solved examples.

What Is Cos Inverse Formula?

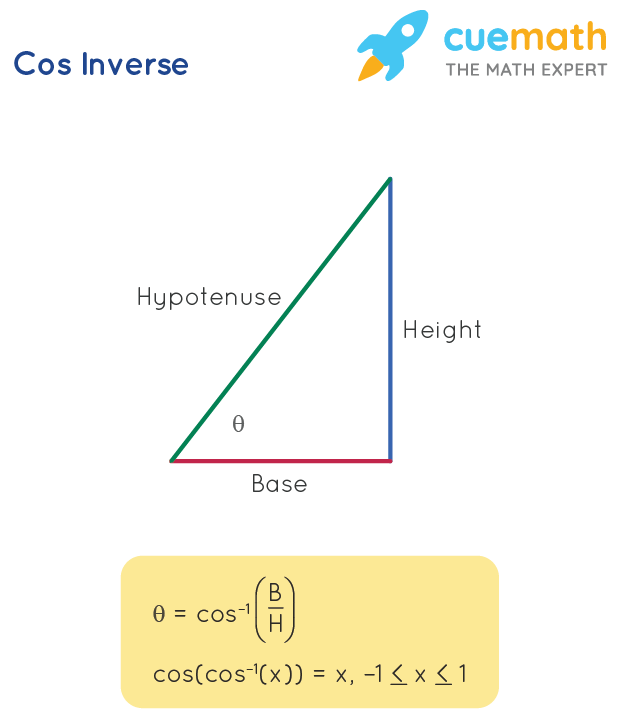
Cos inverse formula is used to find the angle when base and hypotenuse are given. Cos inverse function also possesses some properties regarding its domain and range. The Cos inverse function is also called as “Arc Function”. Cos inverse formula can be given as:

\(\Theta = \cos ^{ - 1} \left(\dfrac{B}{H}\right)\)

\(\cos(\cos ^{ - 1}(x)) = x, -1 \leq x \leq 1\)

where,

• B = Base
• H = Hypotenuse
• \(\Theta\) = angle

Examples Using Cos Inverse Formula

Example 1: In a right-angled triangle ABC, the right angle at B, base AB = 12 inches, and AC = 24 inches. Find angle A in the triangle.

Solution:

To Find: Angle A.
Given:
Base = 12 inch
Hypotenuse = 24 inch
Now, using the cos inverse formula:
\(\Theta = \cos ^{ - 1}(\dfrac{B}{H})\)
 A = \(\cos ^{ - 1}(\dfrac{12}{24})\)
A =  \(\cos ^{ - 1}(0.5)\)
A = \(60^\circ\)

Answer: Angle A will be \(60^\circ\).

Example 2: A ladder 48.5 inches in length is used to climb a 42-inch tall building. Find the angle made by the ladder with the wall of the building to reach its top.

Solution:

To Find : Angle made by the ladder with the wall of the building.
Given:
Base = 42 inch
Hypotenuse = 48.5 inch
Now, using the cos inverse formula:
Now, using the cos inverse formula:
\(\Theta = \cos ^{ - 1}(\dfrac{B}{H})\)
 \(\Theta = \cos ^{ - 1}(\dfrac{42}{48.5})\)
=  \(\cos ^{ - 1}(0.866)\)
= \(30^\circ\)

Answer: The angle made by the ladder with the wall of the building is 30°.