Eccentricity of Ellipse

The eccentricity of ellipse is less than 1. The eccentricity of a ellipse helps us to understand how circular it is with reference to a circle. Eccentricity also measures the ovalness of the ellipse and eccentricity close to one refers to high degree of ovalness.

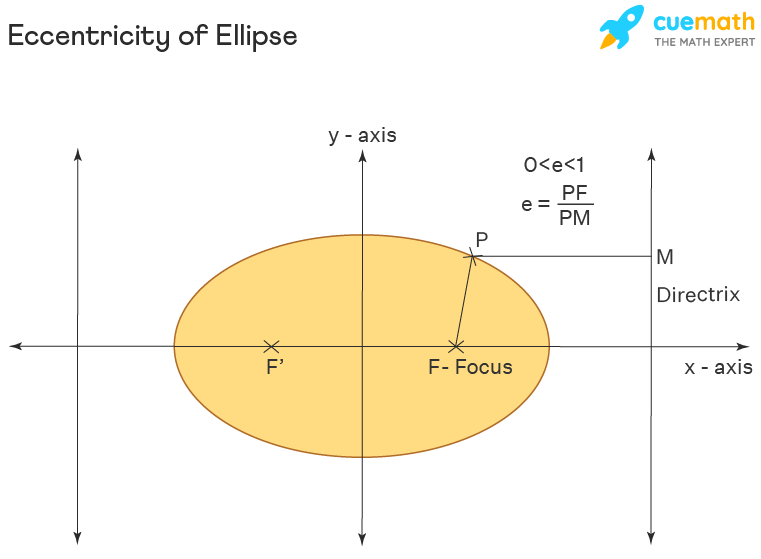
Eccentricity is basically the ratio of the distances of a point on the ellipse from the focus, and from the directrix. Let us learn more about the definition, formula, and the derivation of the eccentricity of the ellipse.

The two important terms to refer to before we talk about eccentricity is the focus and the directrix of the ellipse. For a conic section, the locus of any point on it is such that its ratio of the distance from the fixed point - focus, and its distance from the fixed line - directrix is a constant value is called the eccentricity.

Eccentricity: (e < 1). The ratio of the distance of the focus from the center of the ellipse, and the distance of one end of the ellipse from the center of the ellipse. If the distance of the focus from the center of the ellipse is 'c' and the distance of the end of the ellipse from the center is 'a', then eccentricity e = c/a.

The eccentricity of an ellipse is always less than 1. i.e. e < 1. The eccentricity of an ellipse can be taken as the ratio of its distance from the focus and the distance from the directrix.

Eccentricity = Distance from Focus/Distance from Directrix

.

e = c/a

Substituting the value of c we have the following value of eccentricity.

\(e = \sqrt {1 - \dfrac{b^2}{a^2}}\)

Here a is the length of the semi-major axis and b is the length of the semi-minor axis.

The first step in the process of deriving the equation of the ellipse is to derive the relationship between the semi-major axis, semi-minor axis, and the distance of the focus from the center. The aim is to find the relationship across a, b, c. The length of the major axis of the ellipse is 2a and the length of the minor axis of the ellipse is 2b. The distance between the foci is equal to 2c. Let us take a point P at one end of the major axis and aim at finding the sum of the distances of this point from each of the foci F and F'.

PF + PF' = OP - OF + OF' + OP

= a - c + c + a

PF + PF'= 2a

Now let us take another point Q at one end of the minor axis and aim at finding the sum of the distances of this point from each of the foci F and F'.

QF + QF' = \(\sqrt{b^2 + c^2}\) + \(\sqrt{b^2 + c^2}\)

QF + QF' = 2\(\sqrt{b^2 + c^2}\)

The points P and Q lie on the ellipse, and as per the definition of the ellipse for any point on the ellipse, the sum of the distances from the two foci is a constant value.
2\(\sqrt{b^2 + c^2}\) = 2a

\(\sqrt{b^2 + c^2}\) = a

b² + c² = a²

c² = a² - b²

c = \(\sqrt {a^2 - b^2}\)

e = c/a

\(e = \dfrac{\sqrt {a^2 - b^2}}{a}\)

\(e = \sqrt {1 - \dfrac{b^2}{a^2}}\)

Related Topics

The following topics are helpful for a better understanding of eccentricity of ellipse.

• Coordinate Geometry
• Conics in Real Life
• Cartesian Coordinates
• Parabola
• Ellipse
• Hyperbola

What Is Eccentricity of Ellipse?

The eccentricity of ellipse is less than 1. The eccentricity of ellipse helps us understand how circular it is with reference to a circle. Eccentricity is basically the ratio of the distances of a point on the ellipse from the focus, and the directrix. If the distance of the focus from the center of the ellipse is 'c' and the distance of the end of the ellipse from the center is 'a', then eccentricity e = c/a.

Another formula to find the eccentricity of ellipse is \(e = \sqrt {1 - \dfrac{b^2}{a^2}}\).

Why Is Eccentricity of Ellipse Less than 1?

The eccentricity of the ellipse is less than 1 because it has a shape midway between a circle and an oval shape. The circle has an eccentricity of 0, and an oval has an eccentricity of 1. The eccentricity of an ellipse always lies between 0 and 1. ( 0 < e , 1).

How to Find the Eccentricity of Ellipse?

The eccentricity of ellipse can be found from the formula \(e = \sqrt {1 - \dfrac{b^2}{a^2}}\). For this formula, the values a, and b are the lengths of semi-major axes and semi-minor axes of the ellipse. And these values can be calculated from the equation of the ellipse. x²/a² + y²/b² = 1

What Is the Use of Eccentricity of Ellipse?

The eccentricity of an ellipse is used to give a relationship between the semi-major axis and the semi-minor axis of the ellipse. This major axis of the ellipse is of length 2a units, and the minor axis of the ellipse is of length 2b units. And the semi-major axis and the semi-minor axis are of lengths a units and b units respectively. This can be understood from the formula of the eccentricity of the ellipse. \(e = \sqrt {1 - \dfrac{b^2}{a^2}}\)